川东北碳酸盐岩层地层压力预测方法

李明忠，臧艳彬，方 群，孙平平

(1.中国石油大学(华东)石油工程学院，山东 青岛 266555;2.中国石化石油工程技术研究院，北京 100101;3.中国石油渤海钻探工程公司，天津 300280)

海相碳酸盐岩层已成为世界油气勘探开发的重点，川东北普光地区二叠系长兴组和三叠系飞仙关组是我国目前发现的最优质的碳酸盐岩储层，也是世界上罕见的深部优质储层，具有巨大的勘探潜力［1－2］。但目前对碳酸盐岩层地层压力场的研究依然很薄弱，碳酸盐岩储层勘探开发的迅速发展，给地层压力的预测提出了更高的要求。地层压力的预测方法可分为图解法和公式法［3－4］。图解法有等效深度法、比值法和量板法;公式法可分为依赖正常压实趋势线的公式法(Eaton法、等效深度计算法等)和不依赖正常压实趋势线的公式计算法(Fillippone法等)两类。传统地层压力预测的方法大多只适用于“欠压实”成因的地层，且需要建立在正常压实趋势线基础上，在碎屑岩地层中应用有较好的效果。但川东北地区高压异常的成因复杂多样，快速沉降引起的“欠压实”高压机制在碳酸盐岩层中并不明显，很难符合压实规律［5－7］，导致在碎屑岩地层中应用较好的地层压力预测方法，在碳酸盐岩层中效果较差。基于以上分析的碳酸盐岩层的主要特点，当对其进行地层压力预测时，模型的选择必须具备以下两个方面的条件:一是模型不受压实规律的限制，预测过程不需要建立正常的压实趋势线;二是模型不受高压异常成因的限制，应适用于非“欠压实”机制造成的高压异常地层。

1 碳酸盐岩层地层压力预测方法

弹性波在地层岩石介质中传播的速度与地层物性参数之间存在一定的关系，弹性波的速度是各物性参数共同作用的结果。弹性波速度主要是由组成地层岩石矿物的性质、地层所处的热力学环境(温度和压力)以及地层微构造(孔隙、裂缝)三类因素决定［8］。预测地层压力时，建立弹性波速度与地层压力(或地层有效应力)等地层物性参数之间的关系式，可以避免压实规律和高压异常成因的限制。由于波速的影响因素比较多且影响作用复杂，目前研究主要是在室内物理学实验的基础上获取一些弹性波速的综合模型。在20世纪80年代末，Eberhart-Phillips等人分析室内岩心测试得到大量数据，指出影响声波传播速度的因素主要有孔隙度、泥质含量和有效应力，并给出了纵波速度的经验模型［9］;樊洪海借鉴Eberhart-Phillips等人的研究成果，将综合参数模型用于砂泥岩地层压力的预测［10］，模型具体形式如下:

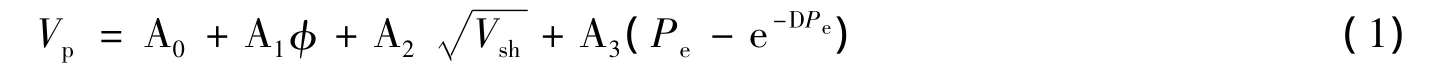
式中，Vp为声波纵波速度，km/s;φ为孔隙度;Vsh为泥质含量;Pe是岩石有效应力，MPa;A0、A1、A2、A3和D分别为模型拟合系数。

该模型的特点为:1)该模型是声波纵波速度与地层物性参数(孔隙度、泥质含量和有效应力)之间的经验关系式，考虑到的波速影响因素比较多。在预测地层压力时，模型不依赖于压实规律，不需要建立正常的压实趋势线;2)此模型适用的范围较广，不受“欠压实”高压机制的限制，可以用于流体膨胀等机制形成的异常高压地层。

鉴于模型以上主要特点，可将综合参数模型应用到碳酸盐岩层地层压力的预测。综合参数模型建立过程中，需要大量数据，包括测井数据、试井数据等。以研究区块内已钻井为研究对象，回归综合参数模型。具体步骤如下:

1)对每口井进行测井数据的处理:由声波速度测井求取碳酸盐层位的声波速度，参考井径曲线消除井径变化造成声波速度的“假异常”;通过GR测井、SP测井获得泥质含量数据;由密度测井或中子测井得到孔隙度数据。

2)由密度测井的散点数据拟合得到上覆岩层压力梯度模型;根据有效应力与泊松比等岩石力学参数之间的统计回归方程，由测井数据计算有效应力。

3)采用逐步回归和多元非线性回归的方法，得到井的综合参数模型系数，进而确定了适合该区碳酸盐岩层地层压力预测的综合参数模型。

4)将新井的孔隙度、泥质含量和纵波速度代入到综合参数模型中，反求岩石有效应力;借助有效应力理论计算新井的地层压力，如图1所示。

2 川东北普光地区碳酸盐岩层地层压力预测

2.1 上覆岩层压力梯度

上覆岩层压力梯度由密度测井数据得到，求某一深度处的上覆岩层压力梯度可按深度进行插值。但当密度测井的井段深度有限时，或是某井没有密度测井数据时，需要利用已有的密度测井的散点数据，回归上覆岩层压力梯度与深度的函数，拟合函数形式如下［11］:

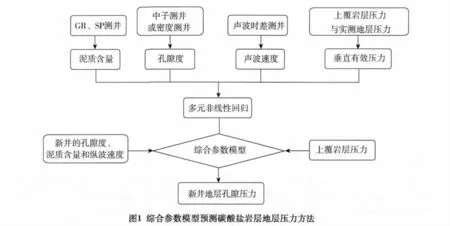
式中，G0为上覆岩层压力梯度，g/cm3;h为井深，km;a、b、c和d为拟合系数。

由普光地区已钻井的密度测井散点数据，经MATLAB拟合，得到该地区上覆岩层压力梯度模型为:

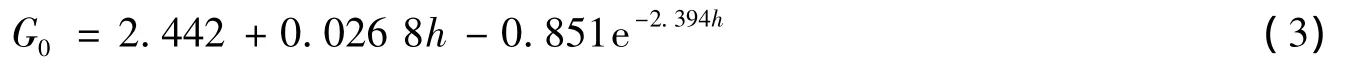
2.2 岩石有效应力的计算

参考川东北地区飞仙关组大量数据，回归得到岩石有效应力与泊松比等岩石力学参数之间的方程［12］:

式中，μ为岩石泊松比;R为拟合度，表征曲线拟合好坏程度。岩石泊松比可利用实测纵、横波时差测井资料计算:

式中，Δts和Δtc分别为纵波时差和和横波时差，s/m。

当缺少横波测井资料时，可借助岩石横波速度与纵波速度之间的关系式［13］(6)计算。

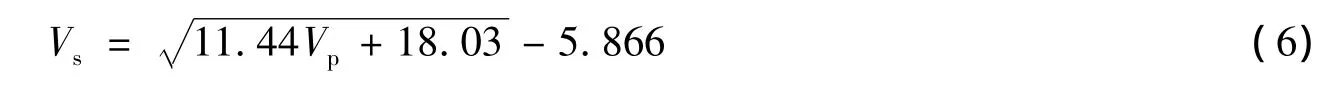
式中，Vs为横波速度，m/s。

2.3 综合参数模型的回归

经过以上的分析和处理，回归综合参数模型所需要的孔隙度、泥质含量和有效应力的数据已经齐备。但单独采用多元非线性回归的方法，初值的设定对模型系数影响大，所得到模型的系数是不稳定的。本文在逐步回归的基础上，采用多元非线性回归的方法最终得到模型合理的系数。

具体过程如下:经分析，系数D随初值的变化最为敏感，因此采用逐步回归的方法，系数D在1～40之间依次取值，D每取一个值，分别得到对应的A0、A1、A2和A3;分析均方根误差，取均方根误差最小的一组作为模型系数拟合的初值。

图2为逐步回归的结果示意图，D=3时均方根误差最小。

初步回归结果为:A0=6.44、A1= －13.2、A2=1.863、A3= －0.692 和 D=3。取该组系数作为多元非线性回归的初值，于是得到符合该井的综合参数模型系数。依照相同的方法研究普光地区其它的井，将各井系数取均值作为该区的综合参数模型系数。

拟合得到普光地区综合参数模型为:

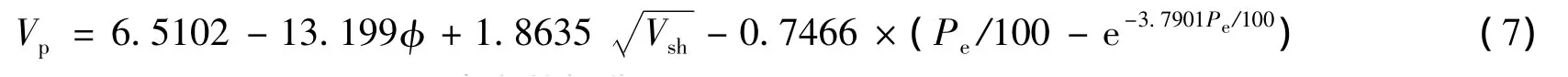
将新井的孔隙度、泥质含量和声波速度数据代入压力预测模型(7)中，反求得到岩石有效应力Pe;上覆岩层压力σ可由式(2)得到，σ=G0gh;进而地层压力由有效应力理论计算，计算式如下:

2.4 模型检验

利用上述方法建立了普光地区地层压力预测模型，并采用未确知有理数方法消除预测压力值突变点，借助加权滑动平均法消除地层压力剖面上的毛刺［14］。将式(4)应用到普光302－3和普光202－1井内的碳酸盐岩地层，比较地层压力的实际测量值与模型预测值之间的关系，如表1所示。

表1 综合参数模型对碳酸盐岩层地层压力预测的检验

从表1可以看出，综合参数模型摆脱了一般地层压力预测方法对压实规律和压实成因的依赖性，在碳酸盐岩层地层压力预测中有很好的效果，预测结果平均精度为5.77%，满足工程需要。用综合参数模型预测地层压力，影响精度的因素有纵波速度受其它地层物性参数的作用、测井数据的准确性等。前者是影响压力预测精度的主要因素，研究纵波速度与地层其它物性参数之间的定量关系将是下一步研究的重点。

3 结论

1)碳酸盐岩层进行地层压力预测时，建立纵波波速与地层物性参数之间的关系模型，可以避免常规方法对压实规律以及高压成因机制依赖的问题。

2)综合参数模型考虑孔隙度、泥质含量和有效应力对声波速度的影响，利用普光地区碳酸盐岩层相关测井、测试等数据，采用逐步回归和多元非线性回归相结合的方法，得到该地区综合参数模型。模型预测的地层压力平均误差在10%之内，满足工程需要。因此，综合参数模型可用于碳酸盐岩层的地层压力预测。

［1］马永生，郭旭升.四川盆地普光大型气田的发现和勘探启示［J］.地质评论，2005，51(4):477－480.

［2］孙钰，钟建华，袁向春.国内湖相碳酸盐岩研究的回顾与展望［J］.特种油气藏，2008，15(5):1－6.

［3］云美厚.地震地层压力预测［J］.石油地球物理勘探，1996，31(4):576－586.

［4］李茂，何俊才，李玮.地层压力的多井对比综合预测技术［J］.特种油气藏，2008，15(1):88－91.

［5］樊洪海.测井资料检测地层孔隙压力传统方法讨论［J］.石油勘探与开发，2003，30(4):72－73.

［6］王存武.川东北地区碳酸盐层系超压发育演化及成因机制［D］.武汉:中国地质大学，2008.

［7］凌代模，钟郎秋.弹性波特性与碳酸盐岩异常地层压力预测［J］.天然气工业，1991，11(6):24－30.

［8］陈颙，黄庭芳，刘恩儒.岩石物理学［M］.安徽:中国科学技术大学出版社，2009.

［9］Phillips DE，Hant DH，Zoback MD.Empirical relationships among seismic velocity，effective pressure，porosity，and clay content in sandstone［J］.Geophysics，1989，54(1):82 －88.

［10］樊洪海.适于检测砂泥岩地层孔隙压力的综合解释方法［J］.石油勘探与开发，2002，29(1):90－92.

［11］樊洪海，张传进.上覆岩层压力梯度合理计算及拟合方法［J］.石油钻探技术，2002，30(6):6－8.

［12］夏宏泉，游晓波，凌忠，等.基于有效应力的碳酸盐岩地层孔隙压力测井计算［J］.钻采工艺，2005，28(3):28－30.

［13］SY/T 5623 －2009，地层压力预(监)测方法［S］.北京:国家能源局，2009.

［14］管志川，窦玉玲，胡清富，等.利用测井资料预测地层压力的误差处理方法［J］.石油钻探技术，2006，34(5):18－20.