20个品种枣树叶面积回归方程的建立

陈宗礼，雷 婷，齐向英，王晓涧，张向前，刘世鹏，薛 皓

(陕西省红枣重点实验室陕西省区域生物资源保育与利用工程技术研究中心延安大学生命科学学院，延安716000)

枣树(Zizyphus jujube Mill)属鼠李科(Rhamnaceae)枣属乔木。其根、树皮 、叶、果实亦供药用。《本草纲目》记载，“大枣，熟则可食，干则可补，丰俭可以剂时，疾苦可以备药，辅助粮食以养民生”。中国枣树栽培历史悠久，资源丰富，有700多个品种，分布极广，集中生长于冀、鲁、陕、豫和晋5省，其产量约占全国总产的90%［1］。陕西是中国枣树发源地和主产区之一。据统计，陕西种植的枣树品种有100多个，其中陕北分布有70多个，仅延川县就有30多个品种［2］。叶片是植物光合作用和蒸腾作用的重要器官［3］。叶片的大小对光能利用、水分蒸腾、生长和衰老、干物质积累、收获量及经济效益有着显著的影响，是生理生化、遗传育种、作物栽培等方面研究经常涉及的内容［4-9］。因此，简单、快速与准确地进行叶面积检测，对指导作物合理密植、群体结构调整、变量施肥和精确喷灌以获得高产具有重要意义;对病虫灾情的准确估计和采取合理的保护措施有着重要的参考价值。测算植物叶面积的方法有多种［10］，方格法操作过程既费时又费工，对于不规则的叶片测量精度大大降低;打孔称重法受叶片厚度、叶龄及叶片含水量的影响很大;叶面积仪测量法，虽测量准确快速，但仪器价格较昂贵［11］。近年来，许多学者通过建立回归方程结合简易测量植物叶长、叶宽达到对植物叶面积进行预测，并用此方法对萝卜、节瓜、南瓜和葡萄等［9，12-19］叶面积进行了研究，取得了较好的应用，但尚未见对枣树叶面积进行回归研究的相关报道。本文通过对延川县20个枣树品种的叶长、叶宽和叶长宽乘积与叶面积的实际测算，并进行回归分析，以期建立可靠的枣树叶面积回归方程，服务于生产和科研实践。

1 材料与方法

1.1 枣叶的采集

2010年8月10号—8月14号，在延川县延水关镇和张家河乡选有代表性的20个生长健壮无病虫害的枣树品种进行叶片采集。采集时分东西南北中五个方向分别采集4个枣吊，每个品种树各采集20个枣吊，标记后装入塑料保鲜袋4℃冷藏箱保存。

1.2 枣叶片的测量

在每个枣吊中部剪取2片成熟叶片，每个品种枣树各取40片叶，平贴于复印纸上并逐一标记。再将贴叶用hp scanjet 2400扫描仪进行扫描;叶片扫描图像的主要参数为:600DPI，JPEG格式存储。然后，将扫描存储于计算机的枣叶图像(如图1)用Image-Pro Plus 6.0软件测量其长、宽及面积［20］，并逐一按品种和叶片序号做好对应的记录工作。

图1 枣叶片扫描图像Fig1 Scanned image of jujube leaves

1.3 枣树叶面积回归方程的建立

利用SPSS17.0统计软件对测量的枣叶数据进行统计分析［21］。先将实测的狗头枣叶片相关数据按SPSS17.0软件程序提示逐一输入计算机;设叶长为x1、叶宽为x2、叶长×叶宽为x3(以下同)，分别做x1与叶面积、x2与叶面积、x3与叶面积的散点分布图，根据散点分布图呈现出的曲线形式，确定回归方程模型，计算出一元回归方程及其相关系数。再分别计算出x1和x2、x1和x3、x2和x3与叶面积的3个二元回归方程和复相关系数以及x1、x2和x3与叶面积的三元回归方程和复相关系数。然后通过对建立的回归方程的相关系数的比较、F检验和回归方程估算及误差检验的方法选出其最佳回归方程。再以同样的方法逐一建立起其他19个品种枣树叶面积的回归方程和枣树总的叶面积回归方程。

2 结果与分析

2.1 狗头枣叶面积的简单线性回归方程

2.1.1 散点图分析 将测得的x1、x2、x3与叶面积的值分别输入计算机，应用SPSS17.0分析功能分别作各自的散点图(图2)。从图2看出，狗头枣叶片的x1、x2、x3与叶面积之间均呈直线关系，其中以x3即叶长×叶宽与叶面积的直线关系最紧密。

图2 狗头枣叶长、叶宽、叶长×叶宽与叶面积的散点图Fig 2 Scatterplot of leaf length，leaf width and leaf length×leaf width with leaf area of Goutou-Zao

2.1.2 一元线性回归方程的拟合 由于狗头枣叶片的x3与叶面积之间的直线相关最好，因此，可按简单直线回归方程模型y=ax+b，建立相应的一元回归方程。利用SPSS17.0数据处理系统中的回归分析功能对叶片进行叶面积对x3的一元回归方程拟合。拟合的回归方程为y1=0.66x3+0.232，计算出x3与叶面积的相关系数为 0.990，F 值达 2080.732(其中 F0.01(1，38)=7.35)，经检验呈极显著相关，表明用该一元回归方程(y1)计算狗头枣的叶面积误差较小，有较好的使用效果。

2.2 二元和三元线性回归方程的拟合

在一元回归分析基础上可继续进行枣叶x1、x2、x3与叶面积的二元和三元回归方程拟合(表1)。

表1各拟合方程的复相关系数经F检验均达极显著水准，其中x1和x3与叶面积、x2和x3与叶面积的二元复相关系数(0.991)相同且最大。表明枣树用y3及y4二元回归方程估算其叶面积有很好的使用效果。由于y4方程的F值稍高，故采用y4方程。

由表1拟合结果可知，x1、x2和x3与叶面积的三元回归的复相关系数达0.992，是对狗头枣进行回归分析所建立的回归方程中相关系数最大的一个，故用三元回归方程y5估算其叶面积准确度更高。

表1 狗头枣叶面积估算的的二元与三元回归方程拟合Table 1 Establishment of binary regression and ternary regression equation of estimated leaves area on Gou-Tou-Zao jujube trees

2.3 回归方程法估算狗头枣叶面积的误差检验

将采集、测量记录的狗头枣树40片叶片的数值带入上述建立的方程y1、y4和y5，分别计算出叶面积值，并与用Photoshop软件测量的实际叶面积进行比较和U检验，结果见表2。由表2可知，用一元回归方程、二元回归方程和三元回归方程计算的叶面积与实测叶面积的差值相互间无显著差异，但三元回归方程y5计算的叶面积差异百分率最小(1.842%)，说明用y5方程计算狗头枣的叶面积，差异较小，准确率高，应用结果更可靠。

2.4 20个品种枣树叶面积回归方程的建立及其特性分析

按照上述建立狗头枣三元回归方程的方法对20个品种枣树叶面积分别进行回归分析和合并回归分析并拟合相应的叶面积三元回归方程。结果见表3。由表3结果可知，各品种枣树叶面积三元回归的相关系数均大于0.95，最高达0.995，经F检验均达到极显著水平。表明枣树各品种用叶长、叶宽和叶长×叶宽与叶面积建立起来的三元回归方程误差最小，使用效果好于其二元与一元回归方程。由20个品种枣树叶片样本测量数据建立的枣树叶面积总的三元回归方程为y6=-0.023x1-0.335x2+0.674 x3+1.145，其相关系数为0.977，经F检验呈极显著相关，说明用其估算不同品种枣树叶面积的准确度也很高，可以作为估算所有枣树叶面积的优化回归方程。

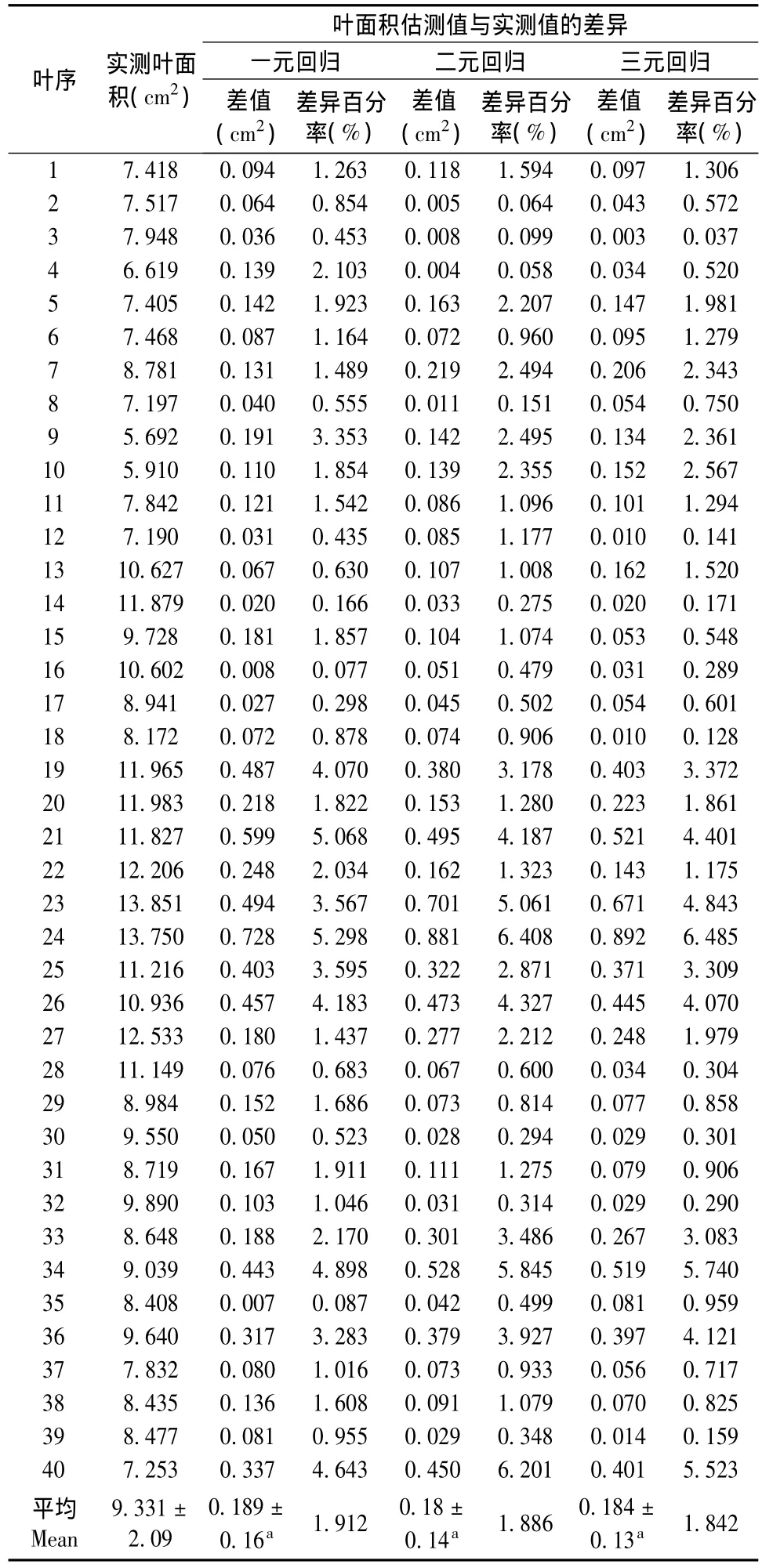
表2 狗头枣叶面积估测值与实测值的比较Table 2 The comparison of estimated value and actual measured value on leaves area from Gou-Tou-Zao jujube tree

2.5 回归方程法测算各品种枣树叶面积的误差检验

将采集、测量记录的各品种枣树40片叶片的数值带入上述建立的方程y5-1～y5-20和y6，分别计算出叶面积值，并分别计算与实际叶面积均值的的差数，进而计算差异百分率并进行U检验。分析结果见表4。由表4看出，用各品种枣叶三元回归方程和总的三元回归方程估算的叶面积与实际叶面积的差值虽在其中7个品种间有显著差异，但U检验的差异百分率均不显著。说明:用各品种的三元回归方程估算各自的叶面积准确率最高;用20个枣树品种叶片样本测值建立起的总的三元回归方程y6估算任一枣树叶面积在实践应用中是简便、可靠和可行的。对20个枣树品种叶面积估算的平均差异百分率为3.03%，95%置信区间为2.5%～3.53%，准确率达96.97%，95%置信区间为96.47% ～97.5%。

表3 枣树叶面积估算的三元回归方程拟合Table 3 Establishment of ternary regression equation of estimated leaves area on jujube trees

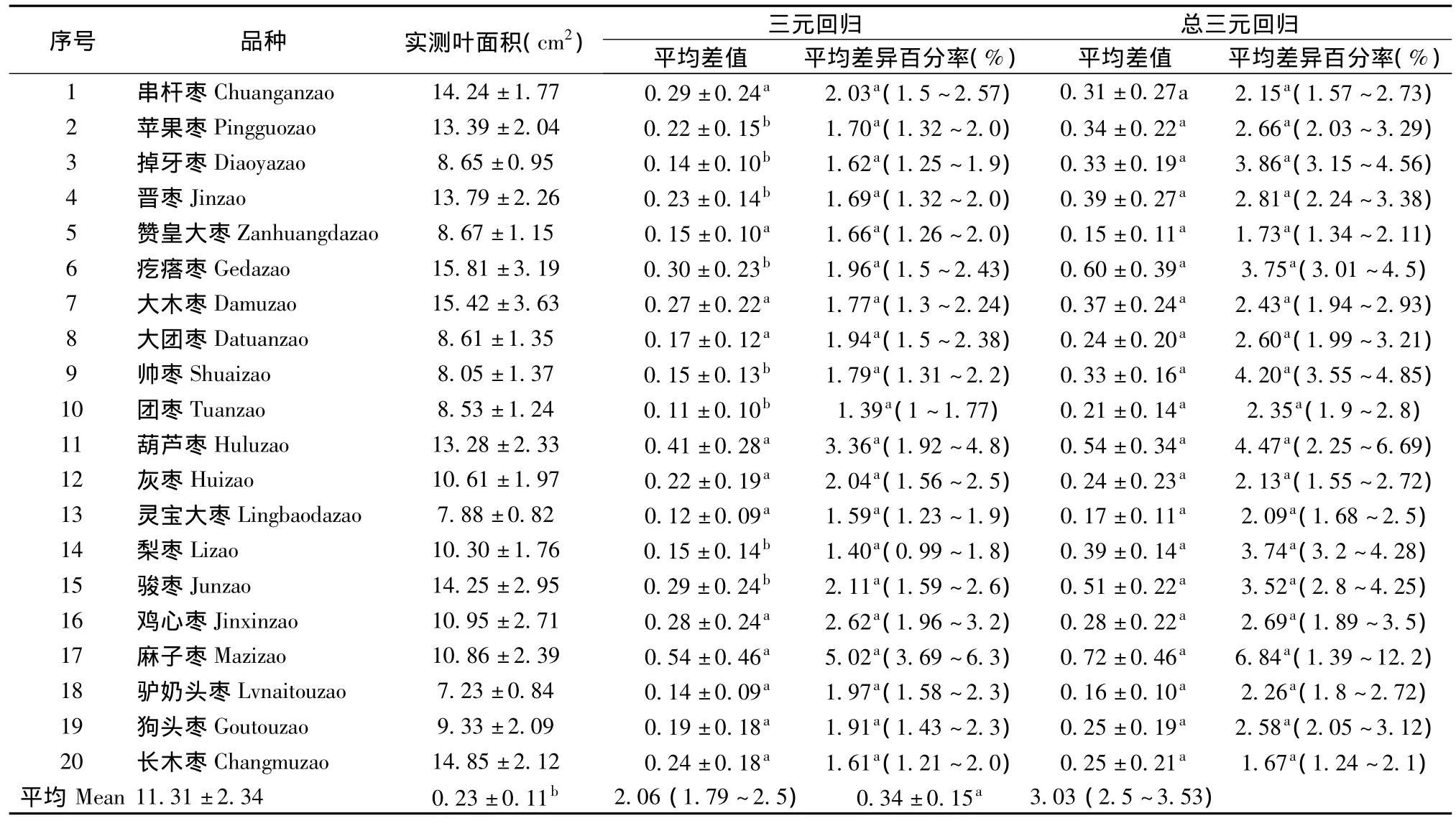
表4 20个枣树品种叶面积估测值与实测值的比较Table 4 The comparison of estimated value and actual measured value on leaves area from 20 species jujube tree

从各品种的三元回归方程估算枣树叶面积的平均准确率上看，估算效果好的品种依次为串杆枣、苹果枣、掉牙枣、晋枣、赞皇大枣、疙瘩枣、大木枣、大团枣、帅枣、团枣、灰枣、灵宝大枣、梨枣、骏枣、驴奶头枣、狗头枣、长木枣，其平均准确率在97.89% ～98.61%之间，估算效果较好的品种依次为葫芦枣和鸡心枣，平均准确率分别为96.64% 和97.38%，估算效果较差的为麻子枣，其平均准确率为94.98%。

从总的三元回归方程估算枣树叶面积的平均准确率上看，估算效果好的品种依次为串杆枣、赞皇大枣、大木枣、团枣、灰枣、灵宝大枣、驴奶头枣、长木枣，其平均准确率在97.57%～98.33%之间，估算效果较好的品种依次为苹果枣、掉牙枣、晋枣、疙瘩枣、大团枣、梨枣、骏枣、狗头枣，其平均准确率在96.14% ～97.42%之间，估算效果较差的品种依次为帅枣、葫芦枣、麻子枣，其平均准确率分别为95.8%、95.53%、93.16%。

3 结论与讨论

3.1 采用扫描叶片并结合Image-Pro Plus 6.0程序的数字图像处理技术和SPSS17.0统计软件对枣树叶面积测量数据进行回归分析，建立了20个品种枣树叶片长、宽以及长×宽对其叶面积的一元回归、二元回归和三元回归方程以及总的三元回归方程。结果表明，用各品种枣树自身的叶宽和叶长建立的叶面积三元回归方程，估算各自的叶面积其估算的准确度最高，估算的平均误差率仅为2.06%，95%置信区间1.79% ～2.5%，是估算各品种枣树叶面积的最佳回归方程。由20个品种枣树的叶片样本测量数据建立的枣树叶面积总的三元回归方程(y6=-0.023x1-0.335x2+0.674 x3+1.145)，估算不同品种枣树叶面积的准确度也很高，对20个品种枣树叶面积估测的平均误差率只有3.03%，95%置信区间2.5%～3.53%，可以作为估算所有枣树叶面积的优化回归方程。

3.2 利用扫描仪和Image-Pro Plus 6.0结合的数字图像处理技术，能快速、准确地测量叶面积，而且不受叶片大小、形状、厚度和人为测量等因素的影响，试验系统误差小精确度高。

3.3 在一元回归中发现，有9个品种枣树的叶长与叶面积相关系数大于叶宽与叶面积的相关系数，有11个品种的叶宽与叶面积相关系数大于叶长与叶面积的相关系数，表明枣树各品种的叶长和叶宽对其叶面积的贡献是不一样的，贡献越大的相关系数就越大，反之越小。这是由各品种枣叶的形状差异引起的，如有的叶形呈规则的椭圆形，有的呈规则的长椭圆形，有的呈不规则的偏椭圆形。

［1］袁亚红，高振鹏，史亚歌.中国红枣的产业化开发［J］.西北农林科技大学学报(自然科学版)，2002，30(9):95-98.

［2］Liu M J，Zhao Z H.Germplasm resources and production of Jujube in China［J］.Acta Horticulturae，2009，840(9):25-31.

［3］李新国，蔡胜忠，李绍鹏.应用数字图像技术测定油梨叶面积［J］.热带农业科学，2009，1:10-13.

［4］赵延明，董树亭，严 敏.玉米叶片叶绿素含量的发育遗传动态及环境互作效应分析［J］.中国生态农业学报，2008，16(3):649-652.

［5］刘晓宇，陆 勇，陈月琴.美洲黑杨苗期叶片主要营养物质含量及苗木生长状况的变异研究［J］.江苏林业科技，2011，1:16-19.

［6］李仙岳，杨培岭，任树梅，等.基于叶面积与冠层辐射的果树蒸腾预测模型［J］.生态学报，2009，29(5):2312-2319.

［7］Li R T，Kojima N，Cui C H.Varietal difference in leaf nitrogen content and leaf area and their effects to ripening rate during mature period of japonica rice［J］.Journal of Northeast Agricultural University，1999，6(2):81-88.

［8］Zhang R H，Kuusk A，Chen C.A new quantitative way for determining leaf area index and net primary productivity in regional scale［J］.Journal of Geographical Sciences，1996，6(4):72-90.

［9］Dobermann A，Pampolino M F.Indirect leaf area index measurement as a tool for characterizing rice growth at the field scale［J］.Communications on Soil Science and Plant Analysis.1995，26(9＆10):1507-1523.

［10］张建新.山茱萸科植物叶面积测定方法的比较［J］.湖北民族学院学报(自然科学版)，2009，27(2):137-140.

［11］柏军华，王克如，初振东.叶面积测定方法的比较研究［J］.石河子大学学报(自然科学版)，2005，23(2):216-218.

［12］Sezer I，Oner F，Mut Z.Non-destructive leaf area measurement in maize(Zea mays L.)［J］.Journal of Environmental Biology，2009，30(5):785-790.

［13］Posse R P，de Sousa E F，Bernardo S，et al.Total leaf area of papaya trees estimated by a non-destructive method［J］.Scientia Agricola，2009，66(4):462-466.

［14］Zhang N，Yui G R，Yu Z L.Simulation of leaf area index and biomass at landscape scale［J］.Journal of Geographical Sciences，2003，13(2):139-152.

［15］张传来，尤 扬，贾文庆.新高梨叶面积测量相关性分析及回归方程的建立［J］.贵州农业科学，2009，37(12):171-174.

［16］冀雅珍.一种新型玉米叶面积估算方法［J］.科技情报开发与经济，2008，18(11):214-215.

［17］李 明，王季槐，沈海亮，等.甘草叶面积的估测方法［J］.贵州科学，2009，27(3):10-19.

［18］卜海东，顾 蔚，齐永平，等.基于图像处理华中五味子叶面积的回归测算［J］.植物生理学通讯，2008，44(3):543-547.

［19］王忠芝，张金瑞.基于图像处理的叶面积测量方法［J］.微计算机应用，2010，31(5):68-72.

［20］佚名.Image-Pro Plus教程［EB/0L］，豆丁网 www.docin.com，2010，8，10.

［21］李志辉，罗 平，洪 楠.Spss for Windows统计分析教程［M］.北京:电子工业出版社，2005，229-238.