沙坑局部含沙水流特性的数值模拟研究

李 健，金中武，杨文俊

(长江科学院河流研究所，武汉430010)

1 研究背景

近年来长江河道中大规模的采砂作业，影响了原始河床结构和涉水设施的安全运行，因此定量地研究河道采砂后形成的沙坑演变具有重要的现实意义。但是，实际情况的采砂沙坑形状极不规则，加上河床本身的演变作用、不间断的采砂作业影响等，沙坑演变的定量研究相当困难。本文将河道和沙坑概化为矩形形状，采用FLUENT流体商业软件对其进行数值模拟研究，定量地研究沙坑对周边水流紊动特性的影响。

FLUENT商业软件在水利工程上已有较多应用［1］，但只是用于水流的精细模拟领域(如溢流堰，大坝效能，水气两相流等)［2－4］，而较少应用于河流动力学领域。主要原因有:①河道边界及地形复杂，且伴随着显著的河床演变，FLUENT不具备河床演变模块;②河流问题涉及的时空尺度较大(长度一般在km级，时间跨度一般在1 a以上)，而FLUENT的计算时间步长受CFL条件限制不能太大，因此计算效率不能满足实际需要;③FLUENT软件模拟自由液面采用VOF法，该方法主要用于局部的水流精细模拟，用于像河流这样的大面积水体模拟，难以满足实际需求。针对以上问题，本文将采用以下方法解决:①概化河床及沙坑边界形状，进行立面二维的水沙模拟，不必考虑复杂边界对流场及沙坑的影响;②采用FLUENT软件中的对称边界条件近似处理自由液面(此处压力、速度、热量通量均为零)，提高计算效率;③充分利用FLUENT软件中的湍流模型和物质浓度求解模型，对沙坑局部进行精细模拟。此外，目前的河流模拟程序求解水沙分布一般采用非耦合的计算方式，即先进行水流计算，再进行泥沙模块计算，没有反映出水沙两相间的相互作用［5－6］，而FLUENT软件中的混合物模型采用耦合方式计算水沙两相流，更接近于实际情况。但耦合计算方式对计算时间步长有限制，并且会影响两相流模型的收敛速度，本文将对两相流耦合模式计算进行详细考察。

采用FLUENT商业软件对河床中沙坑对水沙分布的影响进行数值模拟研究，期望研究成果能对FLUENT软件应用于水沙耦合模拟及今后的河道采砂管理有科学指导意义。

2 沙坑模拟研究

2.1 模拟条件设置

计算区域为具有规则矩形沙坑的河床，如图1。

图1 矩形沙坑示意图Fig.1 Sketch of the river with rectangular sand-pit

模拟河道长度×深度设为5 m×0.6 m，沙坑的长度×深度设为1 m×0.2 m。进口边界给定沿水深方向对数形式的流速分布，即

式中:ux为水流方向流速(m/s);u*为摩阻流速(m/s);y为距离河床的距离(m);Δ为当量粗糙高度(mm)，取Δ=3d90，d90为百分比占泥沙级配90%的床沙粒径(mm)。采用FLUENT软件中的用户自定义函数(UDF)编程进行设置，出口为自由出流边界条件，自由液面边界设置为对称边界，河床糙率设置为0.025，底坡为1‰。计算区域划分为结构网格，沙坑局部加密网格以提高模拟精度。

2.2 混合物模型介绍

FLUENT软件中的混合物模型，可以用来模拟流体中具有其他介质的对流扩散输移问题。混合物模型采用耦合计算模式模拟物质输移现象，反映出物质浓度对流体物理特性(黏性系数)的影响、物质与流体单元动量交换等，但需要在流体中物质的体积浓度不能超过10%的条件下才能使用，否则计算将失稳。长江中下游水体中的含沙浓度较低，满足这一要求，因此采用混合物模型计算是较为合理的。混合物模型的基本控制方程如下:

混合物的连续方程

混合物的动量方程

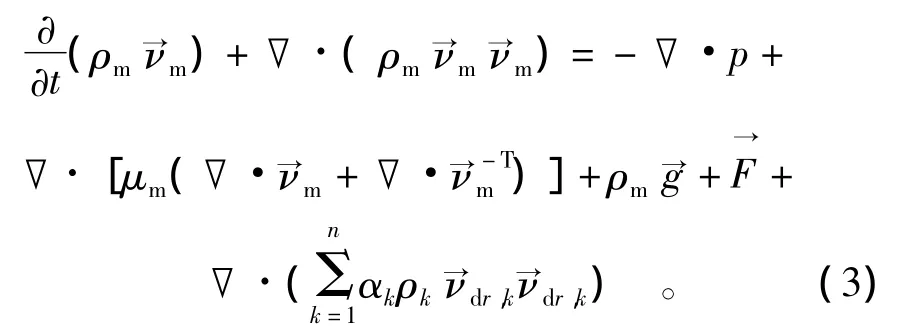
式中:ρm为混合物平均密度为第 k相的体积分数;为体积力;p为静水压力;μm为混合粘性系数是第k相的移动速度

以下将分别进行不含泥沙的清水和含有一定浓度泥沙的浑水2种情况计算，然后分别分析2种计算工况下沙坑周围的水沙特性并进行比较分析。

3 计算结果与分析

3.1 清水计算

图2 计算收敛过程(清水)Fig.2 Convergence process

清水水流计算采用k-ε双方程紊流模型。当动量、流速、紊动动能和紊动耗散率等的计算残差小于一定阈值时，即认为计算收敛，如图2。迭代计算仅为混合物平均速度;300次后以上参数的计算残差均达到很小值，收敛速度较快，其中方量方案的计算残差最小(10－5量级)，而紊动动能和紊动耗散率的计算残差较大一些(10－3量级)。

考察计算收敛后的沙坑局部流场(如图3)，可以看到沙坑的上缘口拐角处产生明显的漩涡，这会不断地冲刷沙坑上缘口处的河床而形成溯源冲刷，当沙坑规模较大时冲刷作用更强，可能危及上游涉水建筑的安全。沙坑下缘口处的水流有从底部向上的流速，也会冲刷下缘口局部的河床泥沙，并在更下游的河床处淤积。如图4，计算的剪切应力分布表明，在沙坑的上、下缘口处较为集中，与流速计算结果的分析相一致。

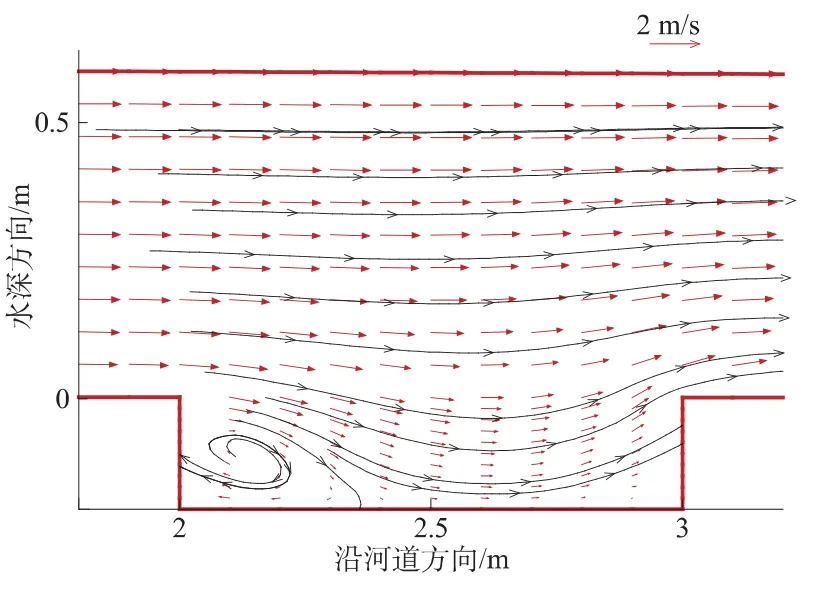
图3 沙坑局部流场Fig.3 Local flow field of the sand-pit

如图5，紊动动能和紊动耗散均在沙坑的上下游边壁处有集中现象，紊动能在下游边壁附近的区域要大于上游边壁区域。沙坑增强了局部河道的紊动能及相应的能量耗散，主要集中在河床与沙坑的交界突变断面处，会造成河床的剧烈冲刷，形成向上游溯源冲刷和下游沿程冲刷的态势。

3.2 混合模型计算

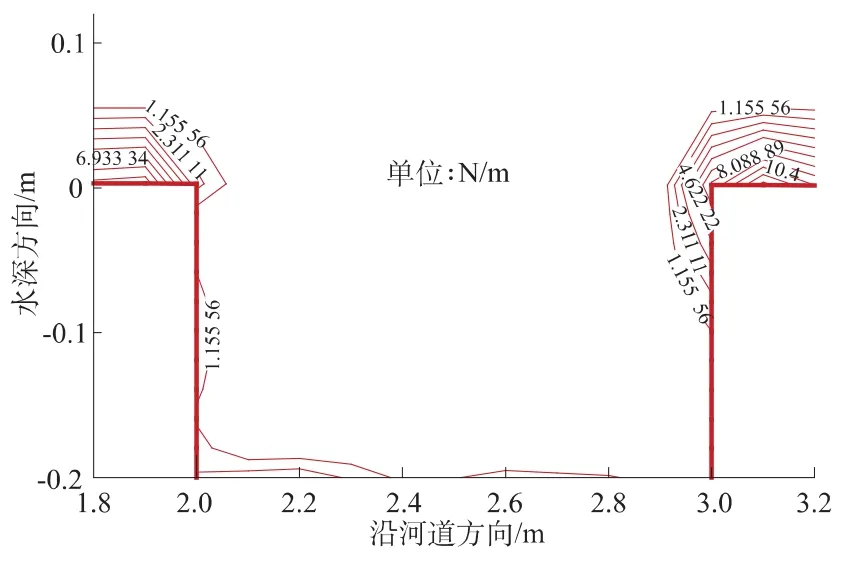
图4 河床处的剪切应力分布Fig.4 Shear stress distribution near the riverbed

图5 清水条件下沙坑局部紊动特性Fig.5 Local turbulent distribution around sand-pit in the absence of sediment

在形成恒定的紊流流场后，应用混合模型对含沙水流进行模拟。进口含沙浓度为2 kg/m3，换算为体积浓度仅为0.075%。在增加了泥沙相后，迭代1 200步计算才收敛(见图6)，并且各项参数(包括动量、流速、紊动动能、紊动耗散和泥沙体积浓度)的计算残差波动较清水的计算要剧烈得多，动量的计算残差较清水的计算收敛时的计算残差要大很多，表明泥沙相对水流的动量影响明显。

如图7，含沙水流的紊动在沙坑底部梯度较大，存在集中区，沙坑上缘口处的紊动比清水时分布均匀，而下缘口处的紊动动能分布2种情况相似。

对比清水和浑水的紊动动能计算分布图5(a)和图7(a)，可发现清水的计算紊动动能分布在0.16～0.58 m2/s2之间，而浑水的紊动紊动动能在0.03～0.28 m2/s2之间。浑水的紊动动能明显减小，并且在水面附近的紊动动能减小幅度要大于沙坑底部的紊动动能减小幅度。

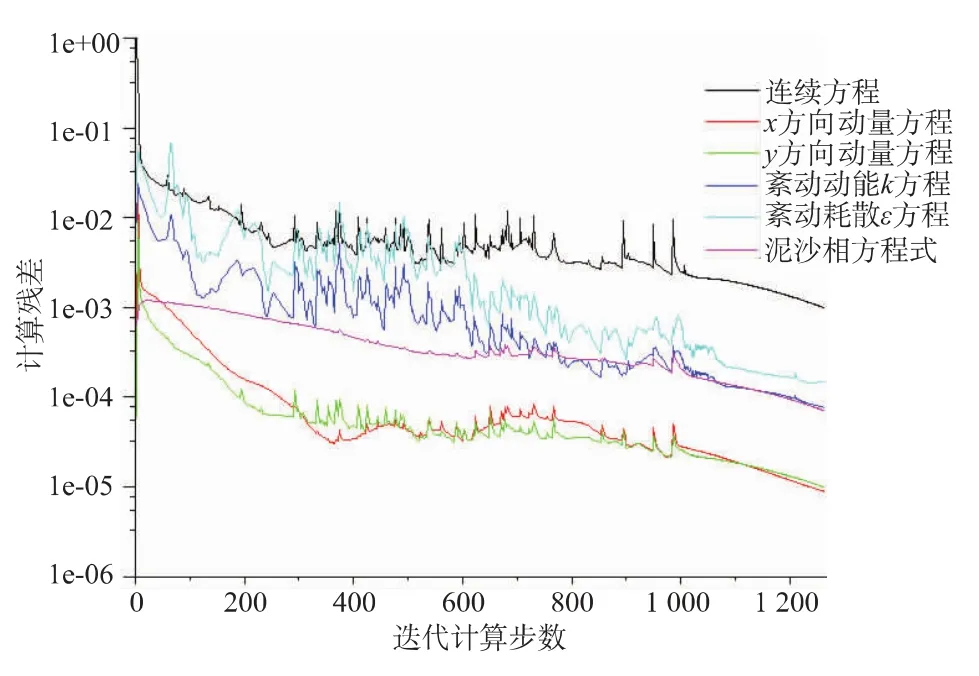
图6 混合物模型计算收敛过程Fig.6 Convergence process of the mixture model

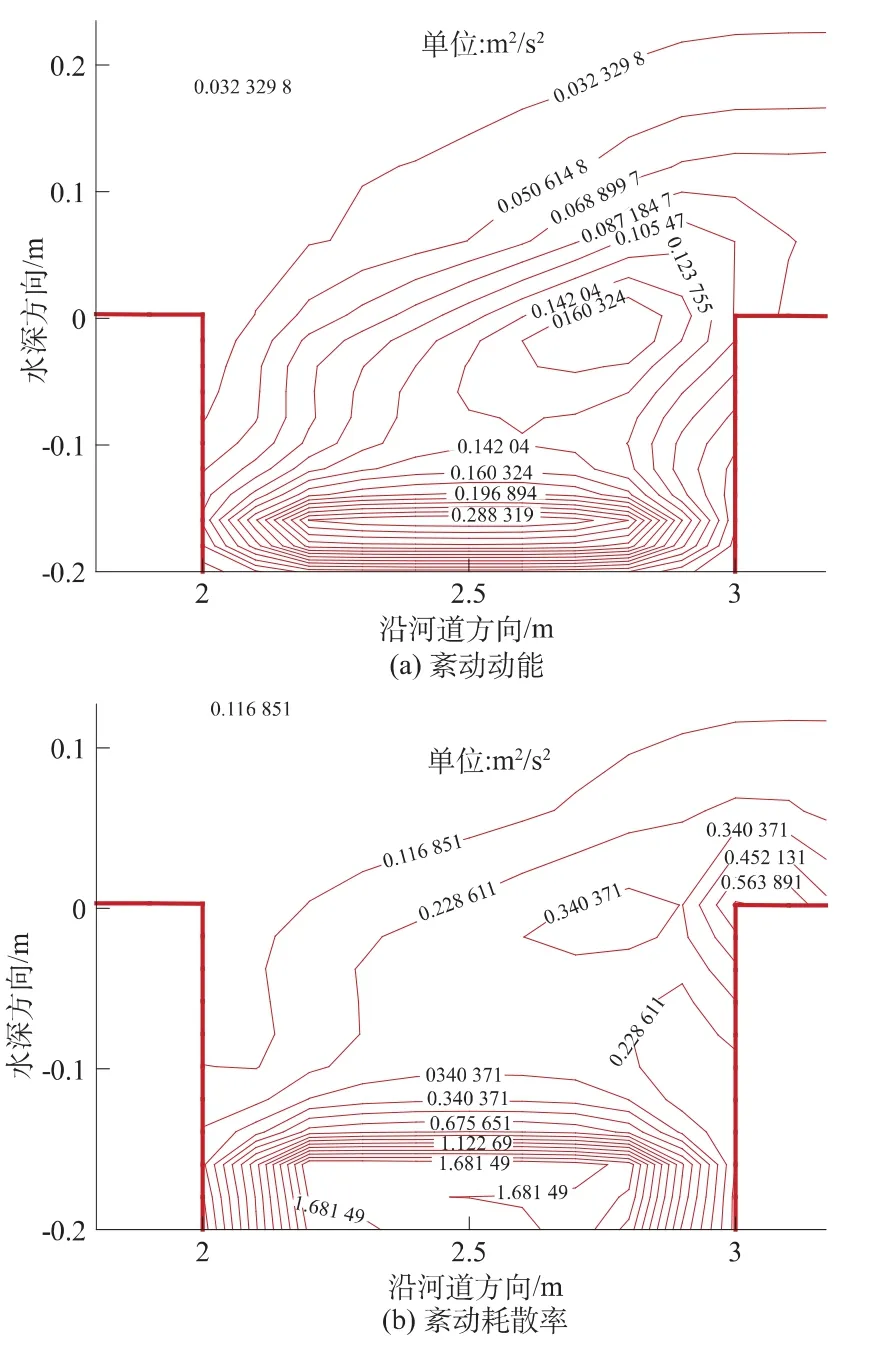
图7 含沙时沙坑局部水流的紊动特性Fig.7 Local turbulent distribution around sand-pit in the presence of sediment

同时清水的紊动耗散也要大于浑水的紊动耗散，可见泥沙的存在抑制了水流内部的紊动以及耗散过程，这一结论与 Cao Zhixian的研究结论一致［6］，说明Fluent软件模拟水沙两相流的可行性和合理性。

如图8，混合物模型对悬移质泥沙的模拟表明:泥沙浓度分布沿水深方向，底部浓度大于表层浓度，与实际情况符合，并且沙坑底部泥沙浓度较高，沙坑下缘口附近的泥沙浓度明显高于上缘口的浓度，说明大量的泥沙会首先在沙坑的下缘口附近淤积。

图8 沙坑局部含沙浓度分布图Fig.8 Distribution of local sediment concentration around sand-pit

4 结论

本文将采砂过程中形成的沙坑概化为规则的矩形沙坑，并应用FLUENT商业软件中的混合物模型对不含泥沙的清水和含沙水流2种情况进行了模拟研究，对比分析了2种工况的计算结果，得到如下结论:

(1)通过编写UDF程序设置FLUENT软件计算的一些边界条件，可以用于具有简单边界的河流动力学领域一些问题的研究，紊动动能和紊动耗散的计算耗时较大。

(2)应用FLUENT软件中的混合物模型可以较好地模拟低含沙水流中的泥沙运动，泥沙相对水流的动量影响明显，并抑制了水流内部紊动，增加了水沙两相流计算收敛难度。

(3)沙坑改变了河流局部流场并在上下缘口附近产生涡旋的次生流，涡旋将造成沙坑上游明显的溯源冲刷和下游沿程冲刷，将对上游的涉水建筑物的安全构成威胁。

［1］叶 茂，伍 超，胡耀华，等.FLUENT软件在水利工程中的应用［J］.水利水电科技进展，2006，26(3):1－7.(YE Mao，WU Chao，HU Yao-hua，et al.Application of FLUENT to Hydraulic Projects［J］.Advances in Science and Technology of Water Resources，2006，26(3):1 －7.(in Chinese))

［2］CHEN Q，DAI G Q，LIU H W.Volume of Fluid Model for Turbulence Numerical Simulation of Stepped Spillway Overflow［J］.Journal of Hydraulic Engineering，ASCE，2002，128(7):683－688.

［3］刁明军，杨永全，王玉蓉，等.挑流消能水气二相流数值模拟［J］.水利学报，2003，(9):77－82.(DIAO Ming-jun，YANG Yong-quan，WANG Yu-rong，et al.Numerical Simulation of Water-Air Two-phase Jet Flow from Flip Bucket to Plunge Pool［J］.Chinese Journal of Hydraulic Engineering，2003，(9):77 － 82.(in Chinese))

［4］周 勤，伍 超，赵元弘，等.“S”型溢洪道水流特性试验与数值模拟研究［J］.水力发电学报，2005，24(3):88 －92.(ZHOU Qin，WU Chao，ZHAO Yuan-hong，et al.Experiment and Numerical Simulation of Flow Characteristics on“S”Style Spillway［J］.Journal of Hydroelectric Engineering，2005，24(3):88 －92.(in Chinese))

［5］COLEMAN N L.Effects of Suspended Sediment on the Open-Channel Flow Velocity Distribution［J］.Water Resources Research，1986，22(10):1377－1384.

［6］CAO Zhi-xian，WEI Liang-yan，XIE Jian-heng.Sediment-laden flow in open channels from two-phase flow viewpoint［J］.Journal of Hydraulic Engineering，ASCE，1995，121(10):725－735.