弯曲航道通航宽度和水流条件确定方法探讨
2013-12-03赵维阳李靓亮茆长胜
赵维阳,李靓亮,茆长胜,李 彪,李 明
(长江航道规划设计研究院,武汉 430011)
1 研究背景
随着水运业越来越受到重视,对航道尺度和航行条件的要求也越来越高,作为研究、设计和施工、维护的一项基本理论和技术,弯曲航道的航道尺度和水流条件标淮是必不可少的。根据对全国内河弯曲航道基本资料的整理和分析,弯曲河段对船舶航行产生的影响主要表现在以下几个方面:①弯曲半径太小或航宽不足;②弯道过渡段枯季淤浅碍航;③弯道凹岸线型不顺、退水淤浅碍航;④弯曲分汊河段的航道问题主要是主支汊的交替发展,使航道变化不定,以及由于通航汊道的年内变化常造成局部水深不足。
我国目前执行的《内河通航标准》(GBJ50139—2004)(以下简称“04 标准”)中[1],仅对弯曲段的航道宽度作出这样的原则性规定,即“内河航道弯曲段的宽度应在直线段航道宽度的基础上加宽,其加宽值可通过分析计算或试验研究确定”。“04标准”没有给出不同航道等级、不同水流条件的弯曲河段适应于代表航行船舶(队)的航道尺度的量化标淮,这样每条河流的弯曲航道都需分析计算或试验,必将带来时间、人力和财力的浪费。为此,本文对弯曲航道尺度和通航水流条件技术标准进行了专门研究,通过研究得到的弯曲航道的航道尺度和通航水流条件技术标准的确定方法,可为水运工程建设、维护标准的确定提供技术支持和科学依据。
2 模型试验
针对弯曲航道对船舶航行的影响及存在的问题,本文主要通过建立弯曲航道概化模型和弯道船模,分析弯曲航道水流条件,研究不同弯曲半径的弯曲航道宽度计算方法和通航水流条件要求。
2.1 模型比尺及尺寸的拟定
由于弯曲航道概化模型同时也为遥控船模试验提供试验场地,故概化模型平面比尺采用船模比尺,即:110,100。模型设计为正态定床模型,故平面比尺和垂直比尺分别为110,100,本次模型试验比尺见表1。

表1 模型试验比尺Table 1 Scales of the model test
2.2 船模概况
船队船型及尺度、船队试验静水航速见表2。通过船模尺度效应修正,可满足船模试验要求。
2.3 试验方案
根据实测资料,建立8个不同弯曲半径的概化模型,其参数见表3,研究在不同流量级、不同航道等级的船舶通航尺度。模型布置见图1(R=280 m)。
(1)流速:由量水堰控制流量,调节尾门控制模型水深,使断面平均流速分别达到3.0,2.5,2.0,1.5,1.0,0.5 m/s。

表2 船队船型及尺度、船模试验静水航速Table 2 Types and scales of the fleet,and speed of the model fleet test in static water

表3 弯曲航道概化模型参数Table 3 Parameters of the generalized model of curved waterway

图1 概化模型平面布置图Fig.1 Plan view of the generalized model
(2)水深:不考虑水深的影响,模型水深控制在20 cm左右。
(3)船模航行方向:由于船舶通过弯道时,下行难度明显大于上行,下行为弯道通航的控制条件,所以主要进行下行试验[2]。
(4)试验组合:根据前面各种因素的变化,进行试验设计,共48种工况。
3 弯曲航道通航宽度
3.1 船舶(队)通过弯道时的偏航距分析与计算
现行《内河通航标准》和《航道整治工程技术规范》(简称《标准》、《规范》)中,均未对弯曲航道偏航距的计算与取值给出明确的规定。据武汉理工大学、天津水运科学研究所、西南水运科学研究所、长江航道规划设计研究院等单位的实船、船模试验研究及经验方法提出了不同的偏航距计算公式和方法[3-5]。
以下采用弯道船模试验,通过理论计算分析方法探讨船舶(队)通过弯曲航道的偏航距P的计算与取值(以下行船队为例)。
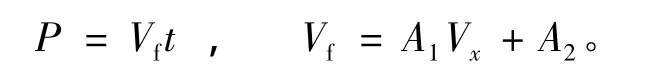
式中:Vf为船队漂移速度;Vx为横向流速;A1,A2为与船型有关的系数;
故有

式中:Vs为船队航速;Vc为水流流速;ø为流向与弯道中心线法线夹角;S为船队航行距离为一个船长L时的漂移量。其中,流向与弯道中心线法线夹角ø可根据航道工程的有关知识求取,

式中:B0为弯曲航道水域河宽(m);R为弯曲航道的曲率半径(m);C为船舶(队)分心航行所占航宽的比例系数,如按四六分心法,则C=0.4。
将上式转换为以A1,A2为变量的二元一次方程,即

根据本次弯道船模试验所得数据,分别计算各种工况下不同尺度船模时的Vs),并以Vcsinø为x轴、为 y轴,绘制曲线图,从而得出线性方程系数,由此得出:
十二驳船队 Vf=0.298 4Vx+0.043 7;
六驳船队 Vf=0.353 7Vx+0.049;
800 t三驳船队 Vf=0.417 1Vx+0.054 7;
140TEU(标箱)集装箱船 Vf=0.489 5Vx+0.061 4;
500 t两驳船队 Vf=0.454 6Vx+0.077 7;
300 t两驳船队 Vf=0.499 3Vx+0.082 4。
根据以上公式计算出相应工况下的偏航距,将其与船模试验值进行比较可看出,各点均匀分布在斜率为1的直线两侧且离散效果较好,这说明计算值与船模试验值吻合较好,见图2。
3.2 弯曲航道加宽值计算与分析
现行《标准》未对弯曲航道宽度作具体规定,现行《规范》规定弯曲段航道宽度应根据弯曲半径、流速、流向、流态、船舶或船队及操纵性能等因素确定。顶推船队,当弯曲半径小于等于3倍设计船队长度时,必须在直线段航道宽度的基础上加宽;当弯曲半径大于3倍设计船队长度,但小于6倍设计船队长度时,应根据水流等具体条件确定加宽值。弯曲段航道加宽值宜通过实船试验确定。当无实船试验资料时,顶推船队弯曲段航道宽度增加值可按下式估算,

式中:ΔB为弯曲段航道宽度增加值(m);R为弯曲半径(m);B为直线段航道设计宽度(m);L为顶推船队长度或拖带船队最大船长(m)。
弯道加宽值ΔB的经验计算公式国外已有很多,常见的有如下几种:
由本次船模试验和以往实船观测成果都证实,上述公式计算的结果偏小,不能满足航行要求,但在实际工作中,凡采用弯道加宽的地方都需要做大量工作,不能单凭公式计算确定[6]。
根据船模试验成果,以及对试验数据和偏航距计算值的分析,我们发现偏航距的大小对弯曲航道通航宽度加宽值 ΔB的取值有直接的影响。因此,绘制在最不利情况下(即流速为2.0 m/s、车档为2.5 m/s时)的弯曲航道通航宽度加宽值ΔB(ΔB=Bz+d1+d2-B单直)与偏航距关系曲线见图3(a),从图中可以看出,加宽值ΔB与偏航距呈线性关系,其线性方程为:ΔB=10.19P -48.8。
考虑到计算公式的适用性和可靠性,绘制各工况下的弯曲航道通航宽度加宽值ΔB(ΔB=Bz+d1+d2-B单直)与偏航距关系曲线见图3(b),从图中可以看出,加宽值 ΔB与偏航距呈线性关系,其线性方程为:ΔB=9.816P -35.1。
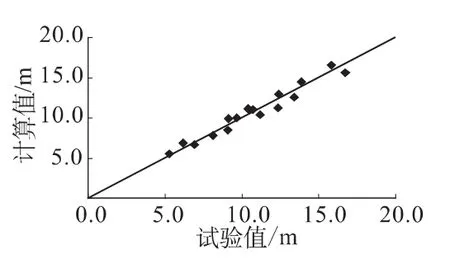
图2 偏航距计算值与船模试验值对比曲线Fig.2 Comparison between the calculated and test value of deviation distance

图3 加宽值与偏航距拟合曲线Fig.3 Fitted curves of widening value and deviation distance
3.3 弯曲航道单向通航宽度的确定
根据船舶(队)在弯道航行所产生的漂角计算弯道宽度,弯道单向通航宽度表达式为

式中:BF为船队下行时航迹带宽(m);d1,d2为船与航道边缘的安全距离(m);P为偏航距(m),按式(3)相关参数计算。
经船模试验观测验证,用上述公式计算的航迹带宽度要比试验观测值的稍小,但总的来说是很接近(见表4),其原因除漂角度量误差外,主要是船模试验时激光反射识别器有不同程度的偏斜。根据船模试验观测,试验观测航迹带宽为计算宽度的1.00~1.03倍。在制订航道标准时,考虑到实际弯曲航道的地形、水流条件等多因素的影响,为使计算出的航迹带宽有一定富裕,在实际计算中对以上值进行修正[7],取1.1。
弯曲段航道中,船到航道边缘的富裕宽度d与直航道相似,但也有不同,它不但要满足视线长度的要求,还要考虑船舶在弯道中航行时向凹岸一侧偏移的现象,因此弯道中的富裕宽度比直道大些。根据全国内河船舶航行轨迹实船观测成果及大量的调查资料分析研究的成果,并参考国外定值原则,d1+d2=(1.5 ~2.0)BS。

表4 用漂角公式计算航迹带宽与船模试验观测值对照(v=2.0 m/s)Table 4 Comparison of track bandwidth between the value calculated with drift angle formula and the observed value from ship model test(v=2.0 m/s)
通过以上计算分析,应用加宽值公式计算弯道航宽与船模试验值对照见表5。从表中可以看到弯道航宽计算值与船模试验值十分接近。
因此,弯道单向通航宽度计算公式改进为

式中:B单直为直线航道宽度(m);P为偏航距(m),按式(3)及图3(b)中相关参数计算。
4 弯曲航道水流条件要求的探讨
4.1 弯曲航道水流条件要求的衡量指标
弯曲河段航道,不仅自然弯曲甚至非常狭窄,限制了船舶通过弯道的航道尺度,增加了船舶操作的难度。目前关于弯曲航道水流条件技术标准,国内外可供查询和参考的资料极少。我国内河通航水流条件技术标准是用水面比降、水流流速、水流流向和流态等指标来衡量的,对于弯曲段航道通航水流条件技术标准来说,用什么指标来衡量,是一个值得探讨的问题。
从本次试验研究结果来看,弯曲段航道通航水流条件的优劣,主要取决于:
(1)水流方向与船舶(队)航行方向。船舶(队)在弯曲段航行时,由于航线与水流方向的不一致,导致水流对船舶航行产生斜向作用,使得船舶(队)偏离航线,而船舶、船队的偏航主要是斜流在航线法线上的分量一横向流速的作用造成的,偏航程度的大小,直接反应了横向流速作用的强弱。可以说,弯曲段航道中横向流速的大小是衡量船舶、船队能否安全航行的重要标准。
(2)水面比降。弯道中水流的水深沿纵向、横向都发生变化,这种不稳定的横向水面高差,必然造成横向流动,并且沿流程而变化的横向流动与纵向主流的迭加,就使水面发生扭曲,影响船舶(队)上驶阻力。
4.2 弯曲航道通航水流条件要求的确定
为了便于分析和衡量斜流对船(舶)队航行的影响程度,将水流流速u分解为航线切线方向的纵向流速uy和垂直于航线切线的横向流速ux,当流速u与航线切线方向之间的夹角为θ时,ux=usinθ,uy=ucosθ。在弯曲航道中产生斜向流速的主要原因是航线与水流流向形成较大的夹角,产生的横向作用对船舶(队)航行具有非常明显的影响。因此,ux,uy是研究弯曲航道通航水流条件的重点。
本次船模试验采用6种船型的船队分别在8种弯曲半径的弯道上,并在4种水流速度、2种车档的工况下进行的弯道通航船模试验,其中弯曲半径为280 m,断面平均流速为2.0 m/s时,弯道最大横向流速为1.42 m/s,弯道横向流速随着断面平均流速的增大而增大,随着弯曲半径的增大而减小。
通过试验研究表明,当船舶(队)尺度和船舶(队)车档一定的情况下,船舶(队)通过弯曲航道航行时,弯道的弯曲半径越小、弯曲航道水流越急,船舶(队)通过弯道时的漂角也就越大,从而导致航迹带宽和所需航道宽度加大,航行难度也越大。
一般情况下,航道的弯曲是产生横向流速的主要因素,对于流速较小的弯曲段航道,一般来说斜流流速一般比主流流速小,因此产生的横向流速也不大,对于弯曲半径较小的弯曲段航道,断面平均流速较大时,其横向流速一般情况下要大,从横向流速与弯曲半径的关系可以看出,当弯曲半径越大,则产生的横向流速则越小,因此,将弯曲段航道水流技术标准分为在不同弯曲半径的情况下进行讨论。

表5 应用加宽值公式计算弯道航宽与试验值对照(v=2.0 m/s)Table 5 Comparison of curved waterway’s navigation width between the value calculated with widening value formula and observed from the test(v=2.0 m/s)
在本试验中,表6中所列船舶(队)通过相应弯曲半径的弯道时,漂角均接近0,航道占宽已和试验航道宽度相近。因此,将最大流量工况下,弯曲半径分别为1 000,600,340,280 m弯道的最大横向流速作为相应弯道的临界横向流速。从表中可以看出,最大流量工况下,弯曲半径为1 000 m的弯道,横向流速大多在1.15 m/s以内;弯曲半径为600 m的弯道,横向流速大多在1.24 m/s以内;弯曲半径为340 m弯道,横向流速大多在1.31 m/s以内;弯曲半径为280 m弯道,横向流速大多在1.42 m/s以内。
其余工况下,船舶(队)均可以很容易地通过弯曲段航道,航行安全基本可以得到保障。
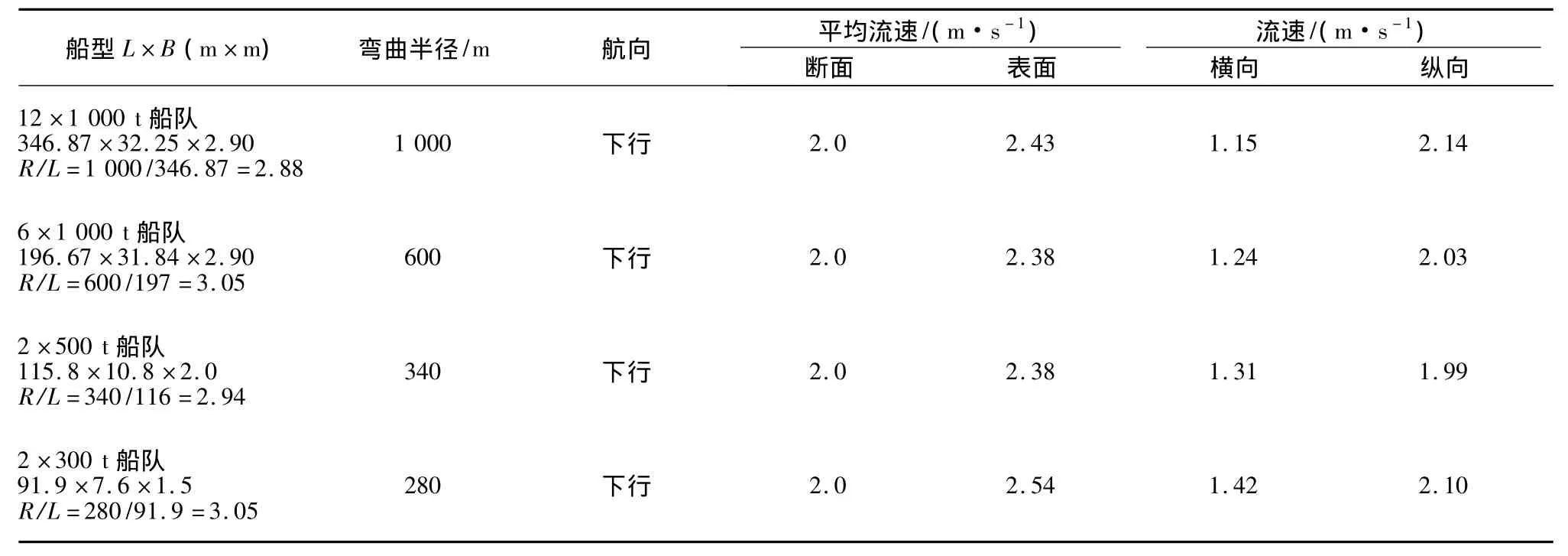
表6 R/L≈3时船模试验观测参数Table 6 Observed parameters of the ship model test when R/L≈3
5 结语
本文通过理论分析,结合有关研究成果、概化模型及船模试验,在分析弯曲航道对通航的影响的基础上,对内河弯曲航道通航宽度进行了分析研究,提出了弯曲航道通航宽度的计算公式,给出了公式中各参数的计算方法,以及分析得出了弯曲航道通航水流条件要求的确定方法,可供水运工程建设参考。因受资料所限,本文所得几点结论仅限于弯曲航道平面问题,为充分掌握船舶弯道航行的特性并指导工程建设,建议对弯曲航道尺度尤其是船舶(队)通过弯曲航道时漂角及偏航距进行深入的研究。
[1]GB50139—2004,内河通航标准及条文说明[S].(GB50139—2004,Navigation Standard of Inland Waterway[S].(in Chinese))
[2]刘 勇,陈厚忠.顶推船队安全过弯的引航模型研究[J].航海工程,2003,(4):45 -46.(LIU Yong,CHEN Hou-zhong.Study on the Navigation Model for the Pushing Fleet to Transit the Bending Channel[J].Ship & O-cean Engineering,2003,(4):45 -46.(in Chinese))
[3]丰慧生.弯曲航道宽度计算的探讨[J].中国河运,1992,(6):47 -50.(FENG Hui-sheng.Discussion of the Calculation of Width of Curved Waterway[J].China Water Transport,1992,(6):47 -50.(in Chinese))
[4]邓年生,王炳奇.弯曲航道平面尺度研究[J].水运工程,2004,(2):74 - 78.(DENG Nian-sheng,WANG Bing-qi.Winding Channels Plane scale Research[J].Port& Waterway Engineering,2004,(2):74 - 78.(in Chinese))
[5]刘明俊,吕习道.船舶过弯道所需航宽建模[J].武汉理工大学学报,2006,(1):178 - 179.(LIU Ming-jun,LV Xi-dao.Necessary Width Model of Ship to Getting Across Channel[J].Journal of Wuhan University of Technology(Transportation Science & Engineering),2006,(1):178 -179.(in Chinese))
[6]李志云,郭国平.关于弯曲河道对船舶通航影响的研究及对策[J].中国水运,2007,(3):29 -32.(LI Zhiyun,GUO Guo-ping.Study of the Curved Inland Effect to the Ship’s Navigation and Its Countermeasures[J].China Water Transport,2007,(3):29 -32.(in Chinese))
[7]王巧洋,黄 勇,张青松,等.内河连续弯曲航道航行漂角分析[J].湖南交通科技,2010,36(2):179-180,183.(WANG Qiao-yang,HUANG Yong,ZHANG Qing-song,et al.Navigation Drift Angle of Inland Continuous Curved Waterway[J].Hunan Communication Science and Technology,2010,36(2):179 - 180,183.(in Chinese))
