倾斜各向异性地层随钻电磁波测井响应模拟

范宜仁，胡云云，李虎，孙庆涛

（1.中国石油大学地球科学与技术学院，青岛 山东266555；2.中国石油大学CNPC测井重点实验室，青岛 山东266555）

0 引 言

斯伦贝谢、哈里伯顿以及贝克休斯等公司相继推出的随钻电磁波测井仪器［1－2］能较好地实现实时随钻地质导向与储层测井评价功能。随钻电磁波测井响应理论大多仍基于各向同性地层模型，实际随钻测井过程中各向异性是影响仪器测井响应的一个重要因素［3］，尤其是在裂缝发育或者薄互层发育的层段，地层所呈现出的宏观各向异性会使随钻电磁波测井响应严重失真，不能有效反映地层信息［4］，给测井储层评价带来了很大的困难。沈金松［5］、王昌学和周灿灿等［6］采用有限差分方法模拟各向异性地层随钻电磁波测井响应，但三维数值模拟计算速度过慢，不适应现场应用。因此，有必要开展基于解析方法的各向异性地层随钻电磁波测井响应快速模拟的研究，为各向异性地层随钻电磁波响应特征研究以及基于随钻电磁波测井的实时地质导向提供支持。本文针对倾斜各向异性地层，进行了基于解析方法的随钻电磁波测井响应数值模拟，并针对地层各向异性系数、仪器发射频率、井斜角等对随钻电磁波测井响应的影响进行了理论分析。

1 原 理

图1为各向异性地层模型。其中，T为发射线圈，R1、R2分别为近接收线圈和远接收线圈；ε1、ε2、ε3为各层的介电常数；μ为磁导率；σ1h、σ2h、σ3h、σ1v、σ2v、σ3v分别为各层的水平电导率和垂直电导率；仪器轴与z轴夹角为α；接收线圈与发射线圈法向均沿仪器轴方向。

电导率张量的Maxwell方程［7］可以表示为

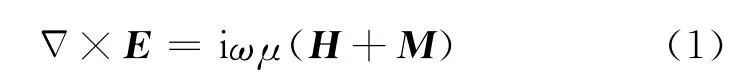
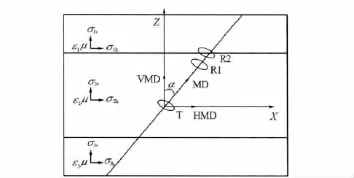
图1 各向异性地层模型

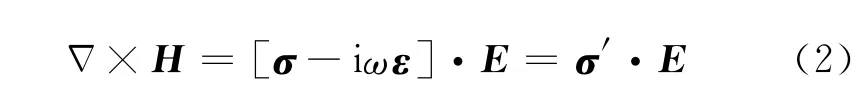
其中，σ′为复电导率张量

定义赫兹矢量位函数

其洛伦兹条件为Δ

对于层状介质中任意方向的磁偶极子源，可以分解为垂直磁偶极子源（VMD）和水平磁偶极子源（HMD）等2个部分［8］，通过赫兹矢量位满足的波动方程分别描述VMD和HMD产生的场，进而基于模型将矢量方程转化为标量方程，再由边界条件确定各层电磁场的解析解。根据法拉第电磁感应定律，接收线圈处的电动势VR为

式中，ω为发射线圈频率；s为接收线圈面积；Hx为接收线圈处总的水平磁场强度；Hz为接收线圈处总的垂直磁场强度。

随钻电磁波测井仪器线圈系的设计均以单发双收的三线圈系为基础结构，通过测量2个接收线圈电动势间的相位差和幅度比转化为相位差电阻率与幅度比电阻率

式中，VR1、VR2分别为近接收线圈与远接收线圈的电动势；arg表示取相位角；Pd为2个接收线圈电位的相位差；Ar为2个接收线圈电位的幅度比。其中，垂直磁偶极子源位函数为

其产生的磁场为

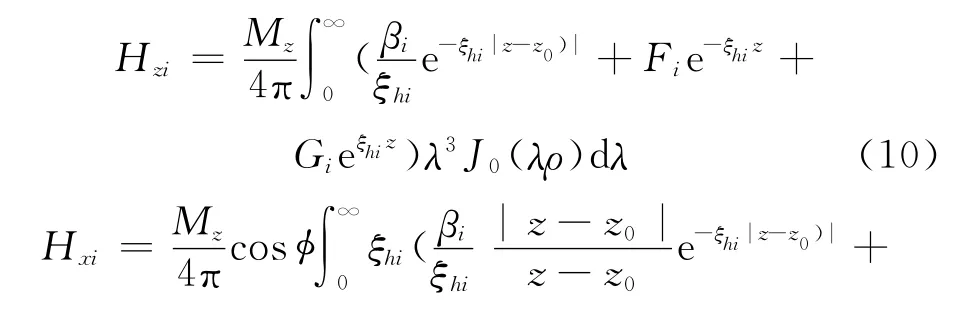
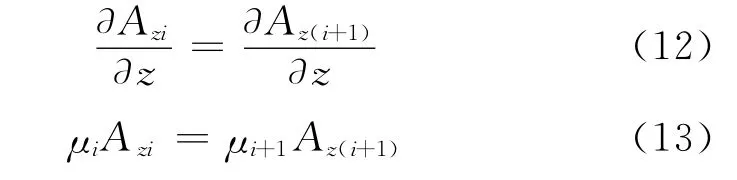
根据边界条件，式（12）、式（13）即可确定各层系数Fi、Gi，进而确定垂直偶极源子产生的磁场分布。

水平磁偶极子源可以分解为TE波与TM波，其中TE波位函数

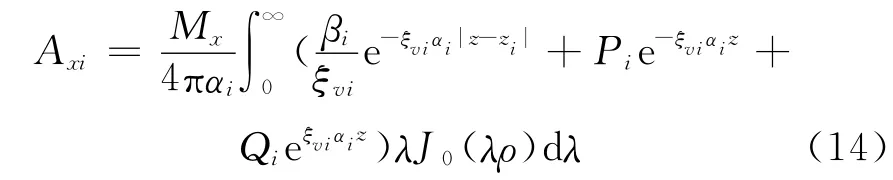
TM波位函数

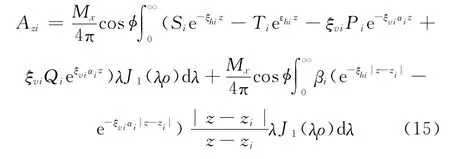
产生的磁场为

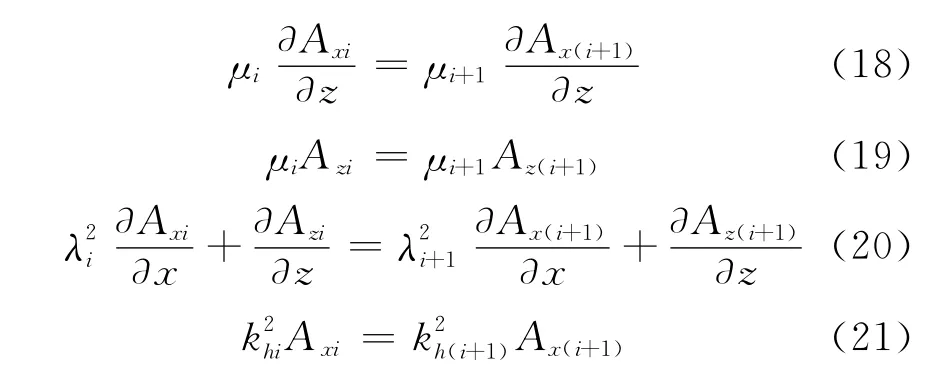
根据边界条件，式（18）至式（21）即可确定各层系数Pi、Qi、Ti、Si，进而求取水平偶极子源产生的磁场强度。

2 含Bessel函数广义积分的求解

2.1 被积函数的收敛性

垂直偶极子源与水平偶极子源磁场［式（10）、式（11）、式（16）、式（17）］的计算均涉及到 Bessel函数的无穷积分；由式（6），接收线圈总的磁场强度为H＝cosαHx＋sinαHz。图2给出了井斜角为0°、45°、75°、80°和85°时H中被积函数实部、虚部与积分变量λ的关系；在低角度时被积函数的震荡性较弱，但随着角度增加，被积函数的震荡性明显增强，夹角小于80°时，积分变量λ达到［0，80］即能满足工程需要；夹角大于80°时，积分变量λ达到［0，200］才能满足工程精度要求。当井斜角为90°时（水平偶极子），被积函数变为完全发散（见图3）。

井斜角小于80°或大于100°时，为了提高积分精度，采用高斯积分［10－11］进行求解；井斜角大于80°且小于100°时，由于积分区间较大，为了加快计算速度，采用Hankel变换［12］对含Bessel函数的广义积分进行求解。

图2 被积函数与λ的关系

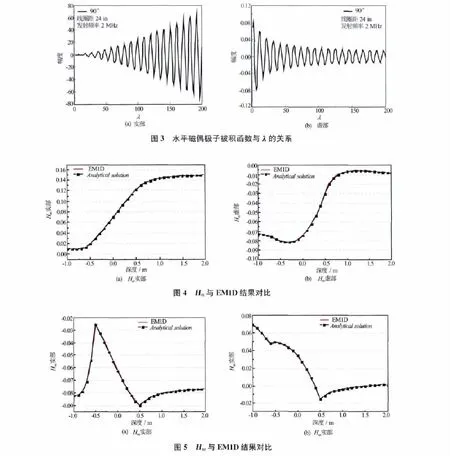
2.2 算法验证

为了验证算法的正确性，针对 Myung Jin Nam［13］给出的线圈结构分别模拟了各向异性地层不同磁场分量Hxx（接收线圈与发射线圈法向皆沿x轴方向）与Hzz（接收线圈与发射线圈法向皆沿z轴方向）响应（结果见图4和图5）。模拟结果与K.H.LeeEM1D的模拟结果［13］能很好地吻合。

3 数值模拟结果与分析

3.1 各向异性地层随钻电磁波模拟测井响应特征

图6、图7分别模拟了各向同性与各向异性三层地层模型随钻电磁波测井响应，其中2个接收线圈的线圈距分别为24in和30in，电阻率各向异性系数定义为各向同性地层中，目的层中离地层界面较远处的视电阻率值与实际地层电阻率值接近，且基本不受井斜角的影响（见图6）。而在各向异性地层中，不同井斜角的视电阻率发生分异，井斜角较小时（井斜角小于30°）视电阻率值基本反应实际水平电阻率，随着井斜角的增大，视电阻率值逐渐向垂直电阻率过渡，且相位差电阻率较幅度比电阻率对垂直电阻率更加敏感；在大斜度井中（井斜角大于70°），由于垂直电阻率的影响，视电阻率曲线在地层界面处产生“犄角”明显大于各向同性地层（见图7）。

3.2 不同各向异性系数随钻电磁波测井响应特征

井斜角较小时（井斜角小于30°）各向异性对视电阻率的影响较小，视电阻率值基本反映实际水平电阻率；井斜角较大时（井斜角大于30°）各向异性（η＞1时）对视电阻率的影响明显，视电阻率值逐渐靠近垂直电阻率，且当各向异性系数η＞3时大斜度井中（井斜角大于80°）相位差电阻率超过垂直电阻率（见图8）。

3.3 发射频率对随钻电磁波测井响应的影响

发射频率越大，视电阻率对地层各向异性越敏感，且相位差电阻率较幅度比电阻率更加敏感。发射频率小于100kHz时，不同频率的幅度比电阻率值几乎一致，而相位差电阻率略有差异；发射频率大于100kHz时，不同频率的幅度比电阻率在井斜角大于50°时才出现差异，而相位差电阻率则在井斜角为30°时即出现较大差异；当发射频率为2MHz时，大斜度井（井斜角大于75°）相位差电阻率已超过垂直电阻率（见图9）。

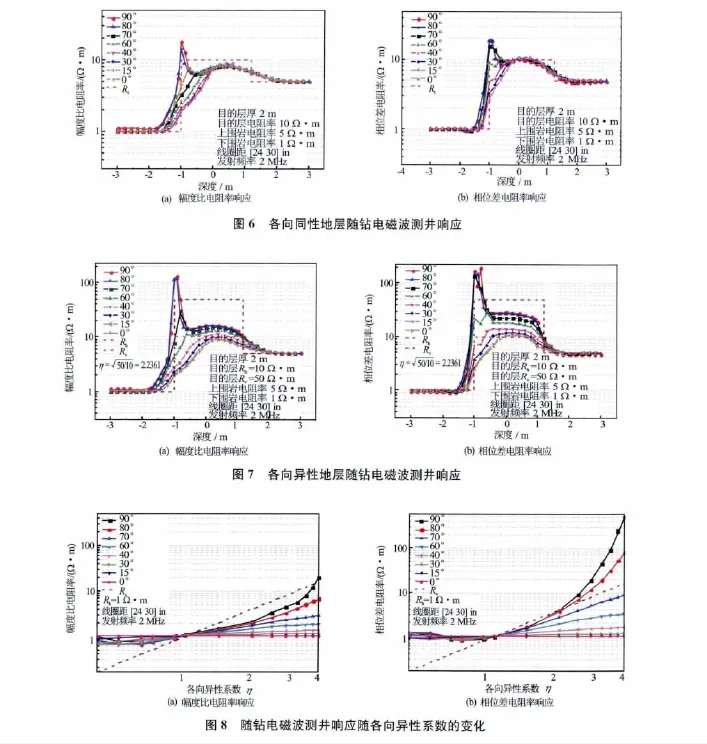
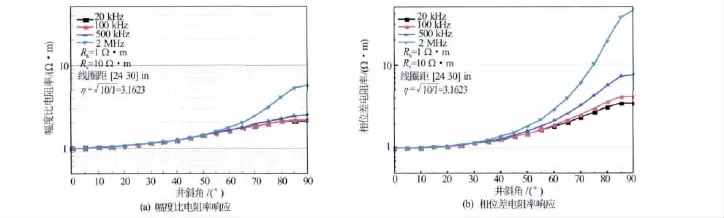
图9 不同频率条件下随钻电磁波测井响应随井斜角的变化

4 结 论

（1）将各向异性地层任意方向的磁偶极子源分解为水平方向与垂直方向磁偶极子源的叠加，采用赫兹矢量位函数对偶极子源产生的磁场进行了描述，基于高斯积分与Hankel变换，分别对不同角度Bessel函数进行求解，克服了被积函数的强震荡性。

（2）井斜角较小时，随钻电磁波测井视电阻率主要反映水平电阻率；随井斜角增大，视电阻率逐渐由水平电阻率向垂直电阻率过渡，且相位电阻率较幅度比电阻率更为敏感；当地层各向异性系数与井斜角较大时，相位差电阻率甚至会超过垂直电阻率。

（3）低频条件下（发射频率小于100kHz）随钻电磁波视电阻率受各向异性影响较小，不同发射频率下的幅度比电阻率几乎重合，而相位差电阻率略有差异；发射频率越高，视电阻率受地层各向异性影响越大，高频条件下视电阻率将远大于低频条件。

［1］ Zhang Z，Gonguet C，Rajani V.Directional LWD Resistivity Tools and Their Business Impacts［C］∥ SPWLA 49th Annual Logging Symposium，Texas：Austin，25－28May，2008.

［2］ Davydycheva S.3DModeling of New－generation （1999－2010）Resistivity Logging Tools，Society of Exploration［J］.Geophysicists，2010，29（7）：780－789.

［3］ Bittar M，Rodney P.The Effect of Rock Anisotropy on MWD Electromagnetic Wave Resistivity Sensors［J］.The Log Analyst，1996，37（1）：20－30.

［4］ Abubakar A，Habashy T M，Druskin V，et al.A 3D Parametric Inversion Algorithm for Triaxial Induction Data［J］.Geophysics，2006，71（1）：G1－G9.

［5］ 沈金松.用有限差分法计算各向异性介质中多分量感应测井的响应［J］.地球物理学进展，2004，19（1）：101－107.

［6］ 王昌学，周灿灿，储昭坦，等.电性各向异性地层频率域电磁响应模拟［J］.地球物理学报，2006，49（6）：1874－1883.

［7］ Li J，Bhardwaj A，et al.Computation of Triaxial Induction Logging Tools in Layered Anisotropic Dipping Formations［C］∥IEEE，2008，46（4）：1149－1163.

［8］ 徐建华.层状媒质中的电磁场与电磁波［M］.北京：石油工业出版社，1997：172－183.

［9］ 其木苏荣，孙丙西.水平层状介质中任意方向磁偶极子的电磁场分布［J］.内蒙古民族大学学报：自然科学版，2004，19（3）：248－256.

［10］ 莫平华.一阶贝塞尔函数广义积分的数值计算［J］.数学理论与应用，2007，27（1）：66－67.

［11］ 张辉，李桐林，董瑞霞，等.利用高斯求积和连分式展开计算电磁张量格林函数积分［J］.地球物理学进展，2005，20（3）：667－670.

［12］ Walter L A.Computer Program Numerical Integration of Related Hankel Transforms of Oders 0and 1by Adaptive Digital Filtering ［J］.Geophysics，1979，44（7）：1287－1305.

［13］ Nam M J，Pardo D，Torres－Verdín C.Simulation of Triaxial Induction Measurements in Dipping，Invaded，and Anisotropic Formations Using a Fourier Series Expansion in a Nonorthogonal System of Coordinates and a Self－Adaptive Hp Finite－element Method ［J］.Geophysics，2010，75（3）：F83－F95.