等效双孔介质电－声曲折度分析及其与弹性参数的关系

葛新民，谢关宝，范宜仁，卢志远，霍宁宁

（1.中国石油大学地球科学与技术学院，山东 青岛266555；2.中国石油大学CNPC测井重点实验室，山东 青岛266555；3.中国石油化工股份有限公司石油工程技术研究院，北京100101；4.中国石油新疆油田公司勘探开发研究院，新疆 克拉玛依834000）

0 引 言

多孔介质岩石的孔隙结构对于非均质复杂储层的测井评价具有重要意义，是储层类型划分、流体识别及储量计算的重要参数。岩石孔隙的曲折度是定量分析孔隙结构及其复杂程度的关键参数之一，国内外学者对该参数开展了大量的理论和实验分析工作。Perkins等［1］推导了电曲折度与电阻增大率和孔隙度的关系；Koponen等［2］建立了曲折度与孔隙度的经验公式；Adisoemarta等［3］认为曲折度是电流传播方向与流体流动方向之间的夹角及胶结指数的函数；Olny等［4］通过声学方法得到了曲折度的表达关系式；Fellah等［5］通过人造玻璃球试验研究了曲折度与孔隙度、孔隙结构的关系；Attia等［6］研究了含水饱和度、孔隙度、胶结指数等对曲折度的影响。本文采用等效双孔介质理论，将复杂的岩石—孔隙系统等效成柱状双孔毛细管模型并引入电、声曲折度概念，采用欧姆定律一维波动方程的线性欧拉解，证明了声、电曲折度的一致性，分析了曲折度的影响因素及其在弹性参数计算中的应用。

1 等效双孔介质模型及电学参数

沉积、成岩及后生改造作用使得储层的原生孔隙受到破坏，导致孔隙类型、孔隙大小及分布的复杂性。对于孔隙－裂缝或孔隙－溶孔系统，其储集空间均可以看成是2组不同性质孔隙的组合，因此，采用双组分孔隙模型进行岩石等效是行之有效的。图1显示的是真实的孔隙结构到抽象的等效双孔介质模型的示意图。图1（a）为某岩心样品的背散射扫描电镜（BSE）照片（黑色部分为孔隙、灰白色部分为骨架，可看出不同大小的孔隙杂乱分布在骨架中），图1（b）为简化后的等效双孔介质模型（圆圈部分代表大孔隙，长条部分代表小孔隙或裂缝）。

图1 等效双孔介质模型示意图

从孔隙拓扑学观点可知，无论是孔隙还是裂缝，都可等效为具有一定直径和长度的直圆柱体。对于等效双孔介质，假设岩石孔隙由大孔和小孔组成，且两者相互连通，则其剖面模型可以简化为相互连通的柱状毛细管模型。图2是双孔介质的等效岩石组分模型［7］。岩石由骨架、大孔隙部分、小孔隙部分（灰色部分代表岩石骨架，白色部分代表不同大小的孔隙）。为了定量描述各孔隙体积，定义孔隙组分比，表示不同孔隙的体积比，即

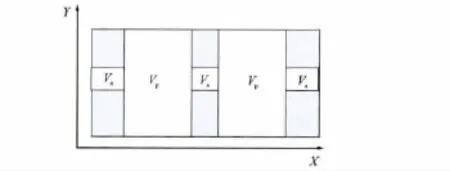
图2 双孔介质的岩石等效组分物理模型

假设大孔隙部分Vp的直径为Dp，横截面积为Sp，孔隙长度为lp；小孔隙部分Va的直径为Da，横截面积为Sa，孔隙总长度为l（见图3），则式（1）可变为

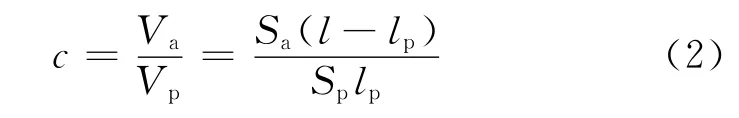
岩石的总孔隙度为

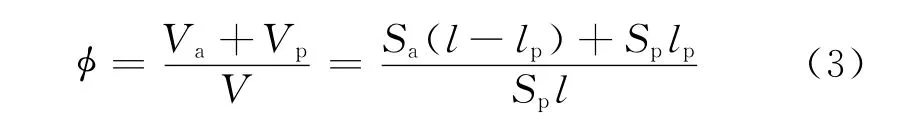
由式（2）和式（3）可得

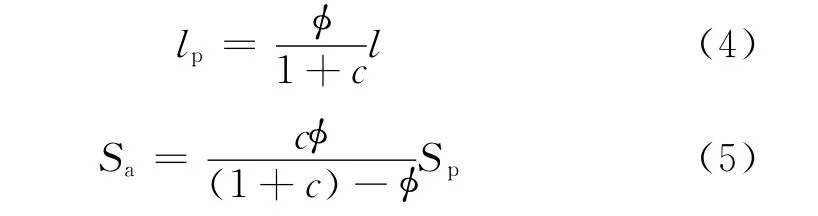
若岩石中不存在导电矿物，根据并联导电原理可得到等效双孔介质岩石的总电阻为

式中，Rw为地层水电阻率，Ω·m；ρp、ρa分别为大孔隙和小孔隙部分的电阻，Ω。

岩石完全含水时的电阻率可以表示为

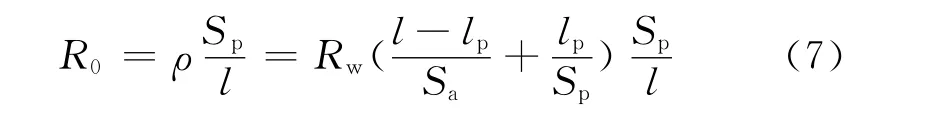
结合阿尔奇公式及式（7）可得到地层因数

从式（8）可知，岩石的地层因数是孔隙组分比c和孔隙度的函数，说明岩石的电学性质不仅受到岩石孔隙度的影响，而且还受到孔隙组分及相对含量的影响。

图3 等效双孔介质剖面参数

Perkins等推导出了电曲折度与地层因数和孔隙度的关系为（其物理模型见图4，图4中L和A分别为岩石的长度和截面积；Lw和Aw分别代表电流通过等效孔道的长度和截面积）［1，8］

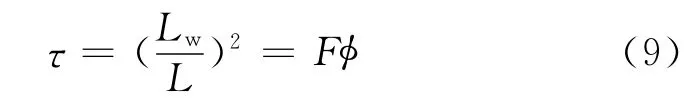
式（9）说明，电曲折度是地层因数和孔隙度的函数，随着地层因数和孔隙度乘积的增大而增大，结合式（8）可知，电曲折度受孔隙组分比和孔隙度的双重影响。

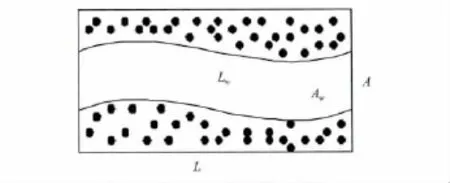
图4 电曲折度岩石等效结构

2 一维波动方程与声曲折度计算

由于多孔介质中孔隙大小、孔隙方向及其与岩层夹角不同，声波在不同的孔隙中存在不同的衰减特征，这种衰减特性与各组分孔隙比例有关。如图1（b）所示，当声压作用在岩石两端时，大孔隙部分发生震动，但小孔隙（裂缝）部分还不能完全发生震动。这可近似认为小孔隙介质的密度要大于大孔隙介质，因此声波在大孔隙中衰减快，在小孔隙中衰减慢。声波在不同孔隙中的衰减差异可用声曲折度ks表示，当声曲折度等于1时，说明大小孔隙内声波的衰减速度相同［9］。

采用归一化的欧拉公式求解一维波动方程。如图2所示，X方向的声波速度可以写成［9－10］

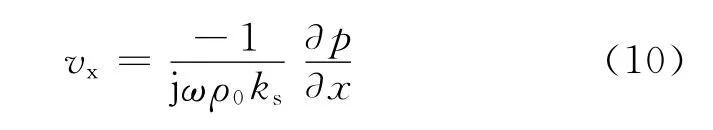
式中，ks为声曲折度；ω为角频率；ρ0为流体密度；p为声压。

对于非黏性流体，双孔介质中各组分孔隙的声波速度方程可以写为

双孔介质中声波速度与孔隙截面积有关，因此，各组分孔隙中的声波速度存在以下关系

由时间平均方程可知，X方向的平均声波速度可以等效为各组分声波速度的体积平均［10］

双孔介质中声压的X方向微分方程可以写为

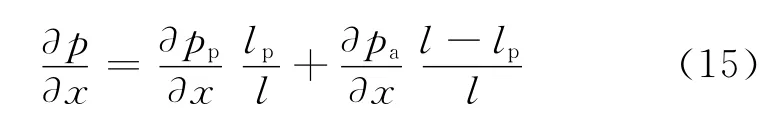
可解出声曲折度ks为

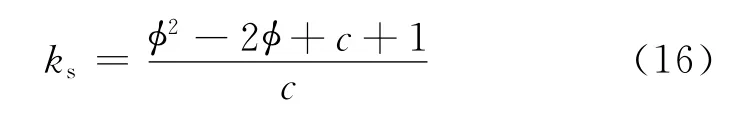
将式（8）代入式（16）替换孔隙组分比c，可得

式（17）表明，声曲折度与电曲折度在数值上是相等的，即电－声曲折度在表征岩石孔隙结构时具有同一性。

3 曲折度影响因素分析及其在岩石弹性参数中的应用

图5是不同孔隙度、不同孔隙组分比时曲折度的变化曲线。从图5中可知，当孔隙度分布在1%～40%之间时，曲折度随着孔隙组分比的增大而呈指数衰减。孔隙组分比从0变化到2时，曲折度衰减最厉害；当孔隙组分比大于2时，曲折度随孔隙组分比的变化幅度非常缓慢。由于孔隙组分比定义为小孔隙体积与大孔隙体积的比值，当岩石以大孔隙组分为主时，随着小孔隙组分的增大，其曲折度变化十分剧烈；但当岩石以小孔隙组分为主时，其曲折度变化十分缓慢，几乎不受影响。从图5中还可以看出，岩石的曲折度随着孔隙度的增大而减小，但其幅度变化非常小，说明影响岩石曲折度的主要因素是孔隙结构而非孔隙度。

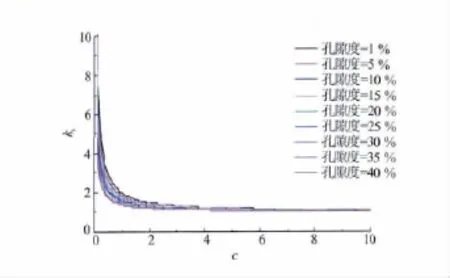
图5 曲折度与孔隙组分比、孔隙度的关系

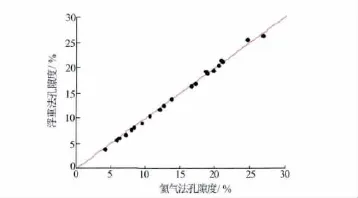
图6 氦气法孔隙度与浮重法孔隙度对比

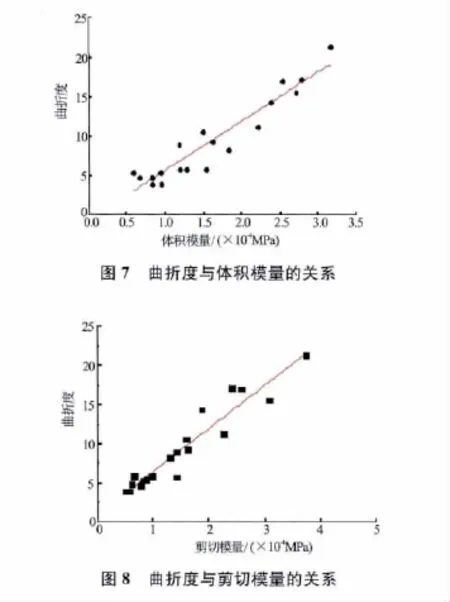
为了研究曲折度与岩石弹性参数之间的关系，选取了我国西部某盆地的孔隙性碳酸盐岩储层的岩心进行了常温常压下的岩石声学、电学参数测试。所取样品岩性为白云岩，其氦气孔隙度分布在4%～26.82%，氦气渗透率分布在（0.036 2～1 210）×10－3μm2之间，非均质性十分严重。为了使岩心完全饱和，采用20MPa恒定压力进行48h的盐水饱和，同时用浮重法测试其孔隙度。饱和盐水为NaCl溶液，浓度为50 000mg／L，测试环境为常温常压（25℃、1MPa），岩心测试结果见表1。岩石的曲折度用式（17）计算。图6为氦气法孔隙度与浮重法孔隙度的对比，两者十分一致，均落在45°线左右，平均绝对误差为0.255%，平均相对误差为1.85%。图7和图8分别是曲折度与体积模量和剪切模量的交会图，从图7、图8可知，曲折度随着体积模量和剪切模量的增大而增大，且呈较好的线性关系，其复相关系数分别为0.904和0.915。经拟合，实验的曲折度（ks）与体积模量（K）和剪切模量（G）的关系为

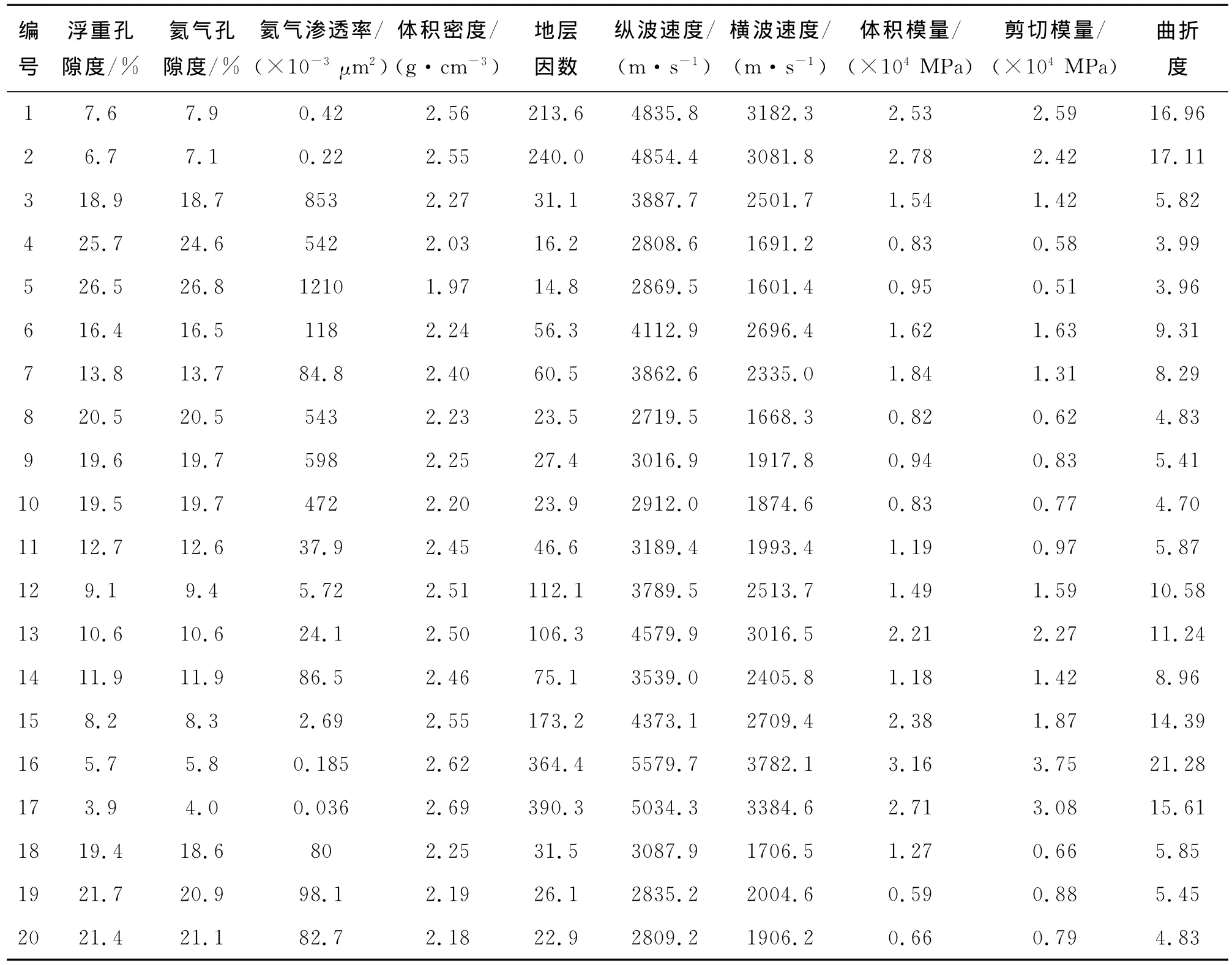
表1 岩心样品声、电测试结果表

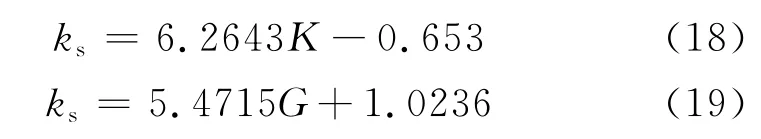
式中，K和G分别代表体积模量和剪切模量，×104MPa。

式（18）和式（19）表明，若已知岩石的电阻率和孔隙度，便可以求得曲折度并可直接通过拟合法得到岩石的体积模量、剪切模量等，进而计算岩石的泊松比、纵横波速度比等其他弹性参数。岩石的体积模量和剪切模量与岩石曲折度的关系可写成通式

式中，a和b分别为拟合参数，不同地区具有不同的值；ks为岩石曲折度；Y为岩石的体积模量或剪切模量，×104MPa。

4 结 论

（1）通过等效双孔介质模拟可知，岩石的电曲折度和声曲折度在数值上是相等的，证明了声曲折度和电曲折度在表征孔隙结构的一致性。

（2）岩石的曲折度主要受控于孔隙结构而非孔隙度。曲折度与孔隙组分比呈良好的指数衰减关系。当孔隙组分比小于2时，曲折度随孔隙组分比的增大而迅速减小，当孔隙组分比大于2时，曲折度随孔隙组分比增大而逐渐减小，但减小幅度非常小。

（3）曲折度与岩石的体积模量、剪切模量存在良好的正相关线性关系。对于声波测井数据不全的井，可通过曲折度进行岩石弹性参数的估算。

［1］ Perkins F M，Osoba J S，Ribe K H.Resistivity of Sandstones as Related to the Geometry of Their Interstitial Water［J］.Geophysics，1956，XXI（4）：1071－1086.

［2］ Koponen A，Kataja M，Timoneny J.Tortuosity Flow on Porous Media［C］∥Phys.Rev.，E Stat.Phys.Plasmas Fluids Relat.Interdiscip，Topics 54406，1996.

［3］ Adisoemarta P S，Anderson G A，Frailey S M，Asquith G B.Historical Use of dmT d and daT in Well Log Interpretation：Is Conventional Wisdom Backwards［C］∥2000SPE Permian Basin Oil and Gas Recovery Conference Proceedings held in Midland，Texas，Soc.Pet.Eng.J.，vol.59699，21－23，March，2000.

［4］ Olny，Xavier，Tran Van，Jerome，Panneton，Raymond.Analytical Solutions for Characterizing Tortuosity and Characteristic Lengths of Porous Material，Using A－coustical Measurements Indirect Model［J］.J.Acoust.Soc.Am.，2001，110：2683.

［5］ Fellah Z E，Berger S，Lavriks W，Depollier C，Aristegui C，Chapelon Y.Measuring the Porosity and Tortuosity of Porous Materials Via Reflected Waves at Oblique Incidence［J］.J.Appl.Phys.，2003，93：9352，

［6］ Attia M Attia.Effects of Petrophysical Rock Properties on Tortuosity Factor［J］.Journal of Petroleum Science and Engineering，2005（48）：185－198.

［7］ 葛新民，范宜仁，杨东根，等.基于等效岩石组分理论的饱和度指数影响因素［J］.石油地球物理勘探，2011，46（3）：477－481，488.

［8］ 雍世和，张超谟.测井数据处理与综合解释［M］.东营：中国石油大学出版社，1993.

［9］ Allard J F.Propagation of Sound in Porous Mediamodeling Sound Absorbing Materials［M］.Elsevier Applied Science，1993.

［10］ Marolf A，Neithalath N，Sell E，Wegner K，Weiss J and Olek J.Influence of Aggregate Size and Gradation on Acoustic Absorption of Enhanced Porosity Concrete［J］.ACI Materials Journal，2004，101（1）：82－91.