岩石介质流动电位影响因素实验研究

卜亚辉，李爱芬，刘均荣，张国浩

（1.中国石油大学石油工程学院，山东 青岛266580；2.中国海油天津分公司，天津300452）

0 引 言

油田生产开发过程中广泛存在流动电位现象，对该效应进行测量解释可以评价地层和流体的性质。这方面的研究引起地球物理界的广泛关注［1－2］，如动电测井、震电勘探、地层流体运移监测等。其中的关键参数是流动电位耦合系数，它的大小直接决定电位信号的大小和测量信号的解释。全面了解电位信号的产生原理，一方面有助于老油田使用自然电位测井曲线和电阻率测井曲线挖掘潜在层位；另一方面将有可能利用该信号实现更远距离的油水前缘预测、地层参数反演，对发展新型动态监测技术具有指导意义。国内学者对该问题进行了若干理论探索和实验研究，1993年原海涵［3］阐述了储层岩石中流动电位的基本理论；2000年房文静等［4］根据物理化学及流动电位的基本原理推导了毛细管中的流动电位计算公式，建立了其与溶液浓度、阳离子交换容量、pH值、饱和度的关系；2010年王军等［5］根据动电耦合理论对岩心渗透率进行测量，结果表明该方法能够较好反映地层渗透性。本文通过整理已有的理论和经验公式，建立了耦合系数随温度和溶液浓度的变化关系，并通过实验对不同浓度NaCl溶液通过不同尺寸石英砂的流动电位效应进行了测量。

1 基本原理

流动电位是一种耦合流动效应，是指电解质溶液在外力作用下通过毛细管或多孔介质时，其两端有电位差产生的现象。其产生原因与电解质溶液与岩石接触面之间形成的双电子层结构有关［6］，其中紧临岩石表面的电荷受到强静电作用力影响，排列紧密且不发生移动被称为紧固层；紧固层之外的电荷排列松散，能够自由扩散并随流体迁移被称为扩散层。当外界存在压力梯度时，扩散层中的电子产生定向移动，从而形成了电流。19世纪初，人们就发现溶液在毛细管流动中存在该现象；1879年Helmholtz提出了双电子层理论；1903年Smoluchowski对Helmholtz公式进行了改进，形成经典Helmholtz－Smoluchowski（HS）公式

式中，Cv为流动电位耦合系数，V／Pa；ΔU为测量电位差，V；Δp为压力差，Pa；μf为流体黏度，Pa·s；εr为流体相对介电常数，无因次；εo为真空介电常数，取8.854×10－12F／m；为流体的电导率，S／m；ζ为Zeta电位，V。

然而式（1）对于岩石这种多孔介质应用时存在问题。由于多孔介质的结构非常复杂，简单的毛细管模型无法反映岩石孔隙大小因素的影响作用。1999年Revil通过考虑岩石表面导电作用建立了流动电位与岩石颗粒大小的关系［7］

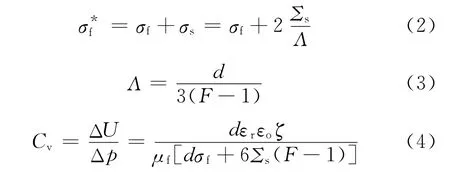
式中，d为岩石颗粒尺寸，m；σs为表面电导率，S／m；Σs为比表面电导，S；Λ为孔隙网络的特征长度，m。可以看出Cv随d的变化关系比较复杂，要满足预测油藏条件下的预测，还需要考虑温度、浓度等对各参数的影响作用。

2 浓度和温度的影响

从式（1）可以看出流动电位耦合系数Cv受4个独立物理量的影响，通过对其讨论，建立与温度和地层水浓度的关系。根据油藏的实际情况（通常温度60～100℃，浓度0.5～2.0mol／L），这里选取了温度20～80℃、浓度0.000 1～2.0mol／L的范围进行计算。

2.1 介电常数

Stogryn给出了岩石介电性质随温度和浓度的变化关系［8］，用式（5）可以计算0≤t≤40℃的值；40℃以上则需要使用外插值公式（9）计算。

式中，εr为相对介电常数，无因次；S为溶液的质量浓度，‰；Cf为溶液浓度，mol／L；t为温度，℃。图1为相对介电常数随浓度和温度变化关系曲线。从图1可见，NaCl溶液电导率随着溶液浓度的升高而降低，当小于0.1mol／L时其变化幅度并不明显，而高于该值后开始缓慢下降；相比之下随温度的变化更加剧烈，温度越高介电性质越弱。

图1 相对介电常数随浓度和温度变化关系曲线

2.2 电导率

电导率反映了溶液对电流的传输能力，是电阻率的倒数，Sen等［9］给出了温度20～200℃、浓度范围0.001～4.7mol／L的 NaCl溶液电导率的随温度和浓度的变化关系

式中，σw为溶液电导率，S／m。从图2可见，当Cf＜0.01mol／L时，溶液浓度和温度的影响很小；当Cf＞0.01mol／L时2个因素均有较强影响，温度越高浓度越大，溶液的电导率越大。

图2 电导率随浓度和温度变化关系曲线

2.3 Zeta电位

Zeta电位指实际参与流动的流体界面上的电位，它从微观层面上决定流动电位的强弱，该参数主要受溶液浓度和pH值的影响。对于油藏通常pH＝6～7.5，Zeta电位显示较为稳定的负值。目前国外众多学者从理论和实验上对该参数进行了讨论，其中Revil［7］从岩石表面的化学反应入手推导了反映该参数公式

式中，kb为Boltzmann常数，1.381×10－23J／K；Tk为绝对温度，K；εf为溶液电导率，F／m；e为元电荷电量，1.602×10－19C；N为 Avogadro常数，6.02×10－23mol－1；Γ0s为表面位密度，m－2；K（－）为矿物表面离解常数，×10－7.2。从图3可见，Zeta电位随着浓度的增大而逐渐趋于0，浓度越低其绝对值越大；温度越高其绝对值越大，但是温度的影响作用只在低浓度才更加明显。

2.4 黏度

温度20～150℃的NaCl溶液黏度随温度和浓度的变化规律可用文献［10］提供的经验公式（13）计算

式中，μf为黏度，Pa·s。从图4中的计算结果来看，同一温度条件下，低浓度时的黏度基本保持恒定，Cf＞0.1mol／L时开始出现上升状态；相比之下温度的影响更为明显，随着温度的增加，溶液的黏度逐渐降低。

3 实验测量

为了实际评价耦合系数Cv随岩石和流体性质变化关系，在实验室条件下通过筛选不同粒径的石英砂，使用一定浓度NaCl溶液充分饱和，测量其稳定流动时的耦合系数Cv，并将测量结果与以上关系式进行了对比分析。

3.1 实验简介

图5 实验测量流动电位装置简图

实验装置如图5所示，填砂管为有机材料制作，管壁预留压力和电位测点。填砂为筛选后一定目数石英砂，实验前用蒸馏水浸泡；饱和及驱替过程用水为蒸馏水配比的NaCl溶液。选用Ag／AgCl参比电极保证测量信号的稳定性，压力传感器的量程10kPa，精度2.5%，实验过程中间隔一定时间测量溶液pH值，确保无明显变化。分别用蒸馏水配比3种浓度0.001、0.01mol／L和0.1mol／L的 NaCl溶液，筛选3种尺寸的石英砂其参数见表1，测量获得了3组流动耦合Cv值。

表1 填砂尺寸及性质参数表

3.2 结果分析

图5至图7是通过以上实验获得耦合系数Cv测量值和20℃时理论计算值取绝对值后对比图。可以看出各溶液浓度下，Cv随颗粒尺寸d的变化趋势一致，都是随着d的增大而增大，但是溶液浓度越低，其增长的幅度越大。该变化趋势可由式（1）和式（2）进行理论分析，当溶液浓度一定时，溶液电导率恒定，对于石英砂这种疏松多孔介质，在总体积相等的条件下，随着颗粒的增大其总的表面积减小，表面导电效应会削弱，从而造成Cv增大；当溶液浓度增大时，从图1至图4可以看出各参数均向着促使Cv减小的方向变化，因而Cv绝对值会随着浓度增加呈现大幅度减小。

从理论公式的拟合看溶液浓度0.001mol／L和0.01mol／L的拟合情况较好，变化趋势基本一致。但是溶液浓度为0.1mol／L的理论计算值差异较大，分析原因可能是高浓度下的流动电位效应已经非常不明显，相同压力梯度下的测量值数值偏小，流动过程中的干扰作用相对更强。从图7可见，该浓度下Cv随d的变化影响已经很小了，说明此时表面导电效应的影响很小，该结论与Glover［11］文献中提出的当溶液浓度高到一定值时，表面导电的作用可以忽略的结论一致。由此认为相对较高矿化度地层水条件下，可以直接使用相对更简洁的HS公式预测耦合系数的大小。

4 结 论

（1）实验室条件下，对不同填砂颗粒尺寸和溶液浓度时的电位耦合系数进行了测量，结果显示相同浓度条件下，随着石英砂尺寸d的增大Cv增大。当浓度增加时，耦合系数绝对值会逐渐趋于0，该变化规律与理论计算结果一致。

（2）预测流动电位经典的HS公式在预测岩石这种多孔介质中的流动时存在，而通过考虑表面导电效应建立起孔隙结构的关系式可以有效弥补不足，但是其使用范围只限制在较低浓度的情况。高矿化度地层水条件下，可以忽略表面导电效应的影响，从而相对简单的HS公式具有实用性。

（3）通过分别建立各物理量随温度和溶液浓度的关系，可以预测耦合系数与这2个因素的变化规律，并能够较好拟合实验结果，对于地层条件下的流体运移产生的流动电位效应解释具有指导意义。

［1］ 杨春梅，李洪奇，陆大卫，等.油田开发过程中的动电现象研究［J］.地球物理学进展，2005，20（4）：1140－1144.

［2］ 金鼎，孙宝佃.动电效应测井研究现状和展望［J］.测井技术，2010，34（4）：309－313.

［3］ 原海涵.流动电位的理论公式［J］.西安石油大学学报，1993，8（3）：17－23.

［4］ 房文静，关继腾，王殿生.用毛管电动—水动力学模型研究储层的流动电位［J］.测井技术，2000，24（2）：92－95.

［5］ 王军，胡恒山，徐小蓉，等.基于动电效应的岩心渗透率实验测量［J］.地球物理学报，2010，53（8）：1953－1960.

［6］ 林智信.物理化学：动力学·电化学·表面及胶体化学［M］.武汉：武汉大学出版社，2003：433－435.

［7］ Revil，Pezard，Glover.Streaming Potential in Porous Media 1：Theory of the Zeta Potential［J］.Journal of Geophysical Research，1999，104（B9）.

［8］ Stogryn.Equations for Calculating the Dielectric Constant of Saline Water［C］∥IEEE Transactions on Microwave Theory and Techniques.1971，8：733－736.

［9］ Sen Goode.Influence of Temperature on Electric－conductivity on Shaly Sands［J］.Geophysics，1992，57：89－96.

［10］ Kestin.Effect of Pressure on the Viscosity of Aqueous NaCl Solutions in the Temperature Range 20～150℃［J］.Journal of Chemical and Engineering Data，978，23：328－336.

［11］ Glover P W J，Nicholas Dery.Streaming Potential Coupling Coefficient of Quartz Glass Bead Packs：Dependence on Grain Diameter，Pore Size，and Pore Throat Radius［J］.Geophysics，2010，75（6）：225－241.