复杂网络免疫策略分析

李向华,王 欣,高 超

(1. 西南大学 计算机与信息科学学院,重庆 400715;2. 吉林大学 计算机科学与技术学院,长春 130012)

网络免疫技术通过保护网络中部分节点以切断病毒传播路径的方式保护网络,是复杂网络传播动力学的主要研究内容,也是抑制病毒传播的有效方法之一[1-5]. 高效的免疫策略不仅对计算机网络适用,对人类社会接触关系网络中的传染病传播和控制也有重要意义[6-7]. 然而,目前对复杂网络免疫策略的分析都是基于单一网络结构,即假设网络中的节点服从单一度分布[8],而异构耦合网络在现实世界中广泛存在,如电网、 交通和通信等系统通常耦合在一起、 互相关联,一个系统的波动即会影响另一个系统的稳定[9]. 如疟疾[10]和H5N1[11-12]为代表的病毒可同时在动物网络(蚊子、 鸟类)和人类接触网络中传播;同一所学校内不同班级同学之间也拥有显著不同的接触模式[13]. 因此,研究这类耦合网络的抗毁性具有重要意义[9,14-15].

判断一种网络免疫策略是否可在网络中有效执行,通常从两方面评价: 1) 策略对网络的保护能力,即评估其对病毒传播的抑制能力;2) 策略的可执行能力,即策略部署需要的前提条件. 优秀的网络免疫策略应首先能有效地抑制病毒的传播,保护网络中大多数节点不被病毒感染;同时必须能克服网络拓扑结构和网络动态性的影响,易于在网络中部署.

1 复杂网络免疫策略分类及分析

复杂网络可用图G=〈V,E〉表示,其中:V表示节点集合;E表示边集合. 网络免疫策略的主要目的是从节点集V中选出一些重要节点注入“疫苗”,阻止该节点被病毒感染,进而阻断病毒进一步传播的路径. 这些被选中的免疫节点用Vp表示,被感染的节点用Vi表示. 为了兼顾免疫成本和效率,优秀的免疫策略应使用少量的Vp即可使Vi数目降到最小. 本文先从计算角度出发,围绕免疫节点发现过程,对比分析现有策略的原理、 特点及问题.

按获取信息程度的不同,目前的网络免疫策略可分为全局免疫策略和局部免疫策略;而按选取依据不同,又可分为基于节点度数、 基于网络介数和基于节点核数的免疫策略.

1.1 基于网络全局信息的免疫策略

节点度数反映了节点在网络中的重要程度,目标免疫策略[1-2]作为全局性策略,根据网络拓扑信息直接选择网络中度数最大的一组节点作为免疫节点,取得了非常好的免疫效果. 而介数反映了节点(边)在特定网络结构中承载的流量,进而反映其通信中转能力[16]. 通常介数大的节点(边)是两个社团的桥梁,如果将节点(边两端的节点)去除,则可将网络分割成多个子网络,进而阻止病毒扩散[17]. 因此,基于介数的免疫策略[17]选取网络中中转能力强的中继节点抑制病毒传播. 图1为不同免疫策略选择免疫节点的示意图. 由图1可见,基于节点介数的免疫策略会选择网络中节点介数最大的V9进行免疫；边介数免疫策略则从边介数最大的边L1和L2两端节点(V5,V7或V9)中随机选择一个免疫. 通过免疫介数大的节点,可将图1网络划分为两个子网络,如果免疫V5或V9,则该策略还能进一步打破上(或下)侧子网络的内部结构,不仅阻止病毒在不同子网络间的传播,而且阻止了病毒在子网络内的传播. 文献[17]通过实验证明：节点介数免疫策略的效率优于目标免疫. 因此,免疫策略不但要保护网络中的重要节点(即度大节点),而且中继节点也要进行免疫才能更好地控制病毒的传播.

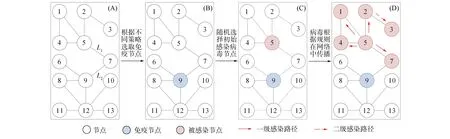
图1 不同免疫策略选择免疫节点的示意图Fig.1 Illustration for immunized nodes selected by different immunization strategies

还有些全局免疫策略通过节点的核数(k-shell或k-core)值[18]选择免疫节点. 当网络中只有单一病毒传播源时,基于核数免疫策略的效率优于目标免疫策略；但当存在多个病毒传播源时,则逊于目标免疫策略[19]. 这是因为基于核数免疫策略选择的节点大多数是网络的核心,聚集在网络的中心位置,而目标免疫选择的节点可分散在网络中的任意位置. 由于本文仿真实验采用多源攻击,因此实验部分并未对比基于核数策略与其他策略的性能差别.

综上所述,虽然全局免疫策略可取得很好的免疫效果,但现实网络大多数是分布式和离散式的,获取整个网络拓扑信息几乎无法实现. 同时,对于一些缺乏集中管理的大规模动态网络,很难获取整个网络信息,为了在效率和可行性之间取得平衡,人们提出了基于局部信息的免疫策略.

1.2 基于网络局部信息的免疫策略

局部免疫策略克服了全局策略需要预先掌握网络拓扑的瓶颈,其中随机免疫策略[1,3]忽略网络节点属性差异,以等概率方式选取一定比例的节点进行保护. 虽然该策略对均匀网络的保护能力较优,但在无标度网络中,该策略几乎需要免疫所有节点才可能阻止病毒传播[1],这在现实世界很难实现.

为提高局部免疫效率,利用现实网络中广泛存在的无标度结构特征,研究者们提出了邻居免疫[4,20-22]和图覆盖免疫[5,23-25]策略. 邻居免疫策略先从网络中随机选取“种子”节点,再从这些节点周围随机选择一个或多个直接邻居进行免疫. 因为在无标度网络中,度大的节点拥有更多邻居,其被选中的概率远高于度小的节点,进而能以较低的计算成本取得远好于随机免疫的效果,同时回避了目标免疫需要掌握全局信息的瓶颈. 但这种对所有邻居不加甄别、 随机选取的方式及仅选取直接邻居的方法,使其效率受到严重制约[23].

基于图覆盖的免疫策略将免疫过程视为一个图覆盖问题,即以“种子”节点为中心,免疫其周围d步范围内的最大度节点. 该方法利用一定局部拓扑知识,取得明显优于邻居免疫的效果. 但由于该策略选择节点行为固定,受网络拓扑,特别是社团结构的影响较大,常陷入局部最优解[26]. 虽然该方法适合于分布式网络,但其计算复杂性随覆盖距离的增加而指数级增大,且在实际应用中,用户很难获得间接邻居信息. 同时,该策略并未考虑任何与应用领域相关的启发信息,也未回答针对不同网络,d值如何选取,因此具有一定的局限性.

为了能仅利用局部信息获得与目标免疫策略近似、 甚至更优的免疫效果,文献[27]从计算角度将网络免疫问题转化成分布式约束优化问题[28],将自组织和正反馈机制融入到分布式约束搜索算法中,提出一种基于AOC的分布式免疫策略. 该策略通过在网络中布置一群具有自治行为的计算体(entity)实现对一组最大度节点的搜索. 与已有方法相比,该方法从群体智能中的激发工作机制入手,通过自组织计算提高搜索效率,但该策略与全局免疫策略的免疫效率有一定差距.

以图1为例,如果只选择一个免疫节点,随机免疫策略可能选择V1作为免疫节点. 如果V1被选为种子节点,则随机邻居免疫策略会从直接邻居V4和V5中随机选取一个作为免疫节点. 而当覆盖范围d=3时,图覆盖免疫策略会将到V1距离小于等于3的{V1,V2,V3,V4,V5,V7,V9}集合中选取一个最大度节点作为免疫节点,即V5或V9;而基于AOC免疫策略中的entity根据它们之间的自组织交互及局部正反馈机制最优移动规则,最终选取V12为免疫节点.

2 同构网络中免疫策略对比及分析

本文以两个真实邮件网络(美国安然公司和西班牙ROVIRA I VIRGILI大学邮件网络)及GLP算法[29]构建的人工网络作为实验用的同构网络,从免疫效率、 代价和鲁棒性三方面定量分析不同类型免疫策略对病毒的抑制能力,所用网络列于表1. 对比免疫相同数目节点时,用网络中最终被感染节点的数目判断哪种策略免疫效率最好;免疫代价不仅比较了各策略的时间复杂度,还分析了免疫临界值,即选择哪种策略可在免疫最少节点的情况下,将病毒传播率控制在最小范围内;鲁棒性则分析对比各策略对网络拓扑变化的适应能力.

表1 实验所用同构网络Table 1 Homogeneous networks used in experiments

2.1 免疫效率

在交互式邮件传播模型[30]中,对比分析目前最具代表的网络免疫策略对病毒传播的抑制能力. 病毒传播模型参数设置与文献[30]相同,传播过程模拟运行600个时间步,初始病毒攻击采用随机攻击方式感染网络中两个节点. 所有数值结果均为运行100次的平均值. 从网络中分别选取5%,10%和30%的节点进行免疫,观察不同策略对病毒传播的抑制能力,即网络的最终被感染节点数目情况.

表2列出了各类策略在合成网络中的免疫效率,括号内的数字表示不采用策略时网络中被感染的节点总数. 由表2可见,在选取相同数目免疫节点的前提下,掌握了全局拓扑信息的节点介数免疫策略对病毒传播的抑制能力最强. 而在全局信息未知情况下,基于AOC策略的免疫效果最佳. 实验结果也表明控制病毒的传播并非只保护网络中度数大的节点,那些传输能力强的中继节点对病毒的传播也起至关重要的作用. 而基于AOC的免疫策略利用自组织和正反馈机制在局域环境中搜索最大度节点的同时,间接免疫了那些具有大度数的中继节点,因而取得了比其他基于节点度数免疫策略更好的免疫效率. 人工社团网络(该网络具有4个社区,由100条边将独立的社区连接在一起)的免疫结果与人工合成网络相似.

表2 人工合成网络中不同免疫策略的免疫效率对比结果Table 2 Immunization efficiencies of different strategies in synthetic networks

图2 人工社团网络最终感染的节点 数目随时间变化曲线Fig.2 Final number of infected nodes with time varying in the synthetic community-based network

图2对表现较优的4种免疫策略做了进一步分析. 其中,节点介数免疫策略明显优于目标免疫策略,这是因为介数免疫可有效破坏网络拓扑,增加网络平均路径长度,切断病毒传播路径. 由于基于AOC免疫策略选择的节点不仅节点度数大,而且介数值高,所以其免疫效率又优于只保护了节点介数大的介数免疫策略.

表3进一步分析了各策略在真实邮件网络中的免疫效率. 图3显示了在安然网络中被感染节点数目随时间的变化过程(A)及被感染节点数目与免疫节点间的变化关系(B). 结果表明,在安然网络中,基于AOC策略在免疫网络中10%的节点后,达到免疫临界点,即病毒很难在网络中大规模扩散. 上述实验结果与人工网络结论相同,即基于节点介数的免疫策略和基于AOC的免疫策略在免疫效率方面取得了比其他策略更好的效果. 由于基于AOC免疫策略只依靠局部信息即可在网络中部署,故更适合在大规模分布式网络中应用.

文献[17]验证了节点介数免疫策略的免疫效率优于目标免疫策略,这是因为介数免疫策略可有效破坏原有网络拓扑结构,通过增加网络平均路径长度的方式阻断病毒传播路径. 而本文实验表明,基于AOC的分布式免疫策略的免疫效率在某些情况下甚至优于节点介数免疫策略. 这是因为基于AOC免疫策略选择的免疫节点不仅具有较大的节点度数,同时搜索自治体在网络中按照网络链路的链接关系进行游走时,会先保护网络中中转能力强的节点,即介数大的节点. 所以基于AOC免疫策略选出的免疫节点不仅具有较大的节点介数值,同时具有较大的节点度数值,因此可更有效地切断病毒传播路径.

表3 真实网络中不同免疫策略的免疫效率对比结果Table 3 Comparison of immunization efficiencies from different immunization strategies in benchmark networks

图3 安然邮件网络的病毒传播示意图Fig.3 Illustration for viruses propagation in Enron email network

2.2 免疫代价

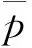
表4 计算复杂性对比结果Table 4 Comparison of computational complex of immunization strategies

由表4可见,基于AOC免疫策略的计算复杂性最小,而全局的介数免疫策略和目标免疫策略因为需要掌握全局拓扑结构才可以实施,因此计算复杂性最大. 在现实应用中,免疫某个节点需要一定成本,为了既能抑制病毒传播,又能降低成本,高效的免疫策略应通过免疫尽量少的节点控制病毒的感染率. 因此衡量免疫代价的另一个指标就是为了达到免疫临界值所需免疫节点比例. 为便于阐述,定义以下变量: ρ0表示不应用免疫策略时网络的最终感染密度(ρ0=NI/N,其中NI表示被感染节点总数);ρf表示应用免疫策略后网络节点最终感染密度;ρ表示病毒传播感染率,ρ=ρf/ρ0. 根据文献[25],定义fc作为免疫临界值,表示为使病毒的传播率ρ→0时,需要免疫的网络节点比例值f.

图4对比了采用随机攻击时,两种人工合成网络中ρ随免疫节点比例f的变化过程. 实验表明,节点介数免疫策略能花费最小的f值有效保护网络;而在分布式策略中,基于AOC的免疫策略免疫代价最小. 以图4(A)为例,当ρ=0.1时,节点介数免疫策略需要的免疫临界值f1小于基于AOC的免疫临界值f2,而f2小于目标免疫临界值f3,即f1

图4 不同幂率结构人工网络中的免疫代价对比Fig.4 Comparison of immunization costs in synthetic networks with different power-law exponents

图5 免疫临界值随网络结构的变化关系Fig.5 Change of immunization critical value (fc) with the network structure

2.3 免疫鲁棒性

面对网络结构差异,同一策略在不同网络中会得到不同的效果,但最佳策略应不受网络拓扑影响,即策略应具有鲁棒性[25]. 图5为免疫临界值fc与网络幂指数之间的变化关系. 由图5可见,fc的变化幅度越小,当网络结构变化时,为抑制病毒传播所需免疫的节点比例变化越小,策略鲁棒性越强. 实验结果表明,节点介数策略的鲁棒性最好,但该策略受网络拓扑结构限制,无法应用于大规模分布式网络中. 而在分布式策略中,基于AOC策略的鲁棒性最好. 同时,该策略的搜索性能所展现的鲁棒性更适用于大规模、 分布式的动态网络[27].

3 异构耦合网络中免疫策略分析

上述病毒传播模型是以同构网络为研究目标,即假设网络节点度分布服从幂律分布. 而现实网络并非拥有单一网络结构,在一个网络中同时包含多个子网络,每个子网络拥有不同的度分布特征,呈现出异构特点[31-33]. 本文构造一个异构耦合网络(heterogeneous interdependent network),并在此网络上分析免疫策略对病毒传播的抑制能力.

异构耦合网络构建过程如下:

1) 构建4个具有独立度的分布网络,分别用G1,G2,G3,G4表示,其中: G1和G2由GLP网络产生器[29]产生无标度网络,幂指数分别为1.7和2.7;G3是利用WS模型构建的小世界网络;G4是利用ER模型构建的随机网络. 表5列出了4个独立网络的结构属性,图6(A)的度分布清晰展现了4个独立网络的异质特性.

2) 在独立网络间随机添加100条边,构建异构耦合网络,如图6(B)所示. 如果网络M和N之间边数用EMN表示,则E12=17,E13=14,E14=14,E23=21,E24=19,E34=15.

表5 异构网络中的子网络结构Table 5 Structures of subnetworks in the heterogeneous network

图6 异构网络示意图Fig.6 Illustration for heterogeneous interdependent network

图7 异构耦合网络中不同免疫策略 的免疫效率对比结果Fig.7 Comparison of immunization efficiencies in the heterogeneous interdependent network

下面仍以交互式邮件传播模型[30]为基础,分析异构耦合网络的抗毁性及各类免疫策略对异构耦合网络的保护能力. 本文先从整个网络中随机选取2个初始感染节点,并根据不同策略要求从网络中选取不同比例的免疫节点. 图7为异构耦合网络中不同免疫策略的免疫效率对比结果. 由图7可见,在异构网络中,虽然基于AOC免疫策略的效率优于其他策略,但低于在同构网络中的效率,表明设计异构耦合网络中的免疫策略是关键.

图8 从不同子网络展开攻击时的病毒传播曲线Fig.8 Virus propagation in each subnetwork of a heterogeneous interdependent network

为进一步分析异构耦合网络的鲁棒性,设定病毒从不同子网络展开攻击,即分别从不同子网络中选取2个节点作为初始感染节点. 图8为应用目标免疫后,病毒在不同子网络中的传播趋势. 由图8可见,无论从何处展开攻击,G3和G4子网络感染速度都最快、 范围最广. 因此,对异构耦合网络中WS和ER子网络的免疫是难点.

综上所述,网络免疫技术是抑制病毒传播的主要方法之一,也是复杂网络传播动力学的主要研究内容. 本文先对网络免疫的基本原理和关键技术进行定性分析,然后在同构网络中定量分析了各策略的免疫效率、 免疫代价和免疫鲁棒性. 实验结果表明,免疫策略对同构网络的保护能力与其计算量近似成反比. 如随机免疫策略与其他5种免疫策略相比,计算量最小,但对网络的保护能力最弱；而基于介数的免疫策略计算量最大,但该策略利用中心控制选择节点(边)介数最大的节点进行免疫,可实现最好的免疫效率,高效阻断病毒传播路径. 本文构建了一种新型异构耦合网络,并分析了免疫策略对异构耦合网络的保护能力,实验结果表明,已有各类免疫策略对异构耦合网络的保护能力有限,设计一种适合异构耦合网络的分布式网络免疫策略是一个亟待解决的问题.

[1] Pastor-Satorras R,Vespignani A. Immunization of Complex Networks [J]. Physical Review E,2002,65(3): 036104.

[2] CHEN Yi-ping,Paul G,Havlin S,et al. Finding a Better Immunization Strategy [J]. Physical Review Letters,2008,101(5): 058701.

[3] HU Ke,TANG Yi. Immunization for Scale-Free Networks by Random Walker [J]. Chinese Physics,2006,15(12): 2782-2787.

[4] Cohen R,Havlin S,Ben-Averaham D. Efficient Immunization Strategies for Computer Networks and Populations [J]. Physical Review Letters,2003,91(24): 247901.

[5] Echenique P,Gomez-Gardenes J,Moreno Y,et al. Distanced Covering Problem in Scale-Free Networks with Degree Correlation [J]. Physical Review E,2005,71(3): 035102.

[6] Cornforth D M,Reluga T C,Shim E,et al. Erratic Flu Vaccination Emerges from Short-Sighted Behavior in Contact Networks [J]. PLoS Computational Biology,2011,7(1): e1001062.

[7] Ames G M,George D B,Hampson C P,et al. Using Network Properties to Predict Disease Dynamics on Human Contact Networks [J]. Proceedings of the Royal Society B,2011,278: 3544-3550.

[8] GAO Jin-xi,Buldyrev S V,Havlin S,et al. Robustness of a Network of Networks [J]. Physical Review Letters,2011,107(19): 195701.

[9] Vespignani A. Complex Networks: The Fragility of Interdependency [J]. Nature,2010,464: 984-985.

[10] Menach A L,Tatem A J,Cohen J M,et al. Travel Risk,Malaria Importation and Malaria Transmission in Zanzibar [J]. Science Report,2011,1: article number 93.

[11] Rivas A L,Fasina F O,Hoogesteyn A L,et al. Connecting Network Properties of Rapidly Disseminating Epizoonotics [J]. PLoS One,2012,7(6): e39778.

[12] Bonté B,Mathias J D,Duboz R. Moment Approximation of Infection Dynamics in a Population of Moving Hosts [J]. PLoS One,2012,7(12): e51760.

[13] Stehlé J,Voirin N,Barrat A,et al. High-Resolution Measurements of Face-to-Face Contact Patterns in a Primary School [J]. PLoS One,2011,6(8): e23176.

[14] LI Wei,Bashan A,Buldyrev S V,et al. Cascading Failures in Interdependent Lattice Networks: The Critical Role of the Length of Dependency Links [J]. Physical Review Letters,2012,108(22): 228702.

[15] Hasegawa T,Konno K,Nemoto K. Robustness of Correlated Networks against Propagating Attacks [J]. The European Physical Journal B,2012,85: 262.

[16] Narasimhamurthy A,Greene D,Hurley N,et al. Partitioning Large Networks without Breaking Communities [J]. Knowledge and Information Systems,2010,25(2): 345-369.

[17] Holme P,Kim B J,Yoon C N,et al. Attack Vulnerability of Complex Networks [J]. Physical Review E,2002,65(5): 056109.

[18] Carmi S,Havlin S,Kirkpatrick S,et al. A Model of Internet Topology Usingk-Shell Decomposition [J]. Proceedings of the National Academy of Sciences of the United States of America,2007,104(27): 11150-11154.

[19] Kitsak M,Gallos L K,Havlin S,et al. Identification of Influential Spreaders in Complex Networks [J]. Nature Physics,2010,6: 888-893.

[20] Gallos L K,Liljeros F,Argyrakis P,et al. Improving Immunization Strategies [J]. Physical Review E,2007,75(4): 045104.

[21] WANG Bing,Aihara K,Kim B J. Comparison of Immunization Strategies in Geographical Networks [J]. Physics Letters A,2009,373(42): 3877-3882.

[22] Holme P. Efficient Local Strategies for Vaccination and Network Attack [J]. Europhysics Letters,2004,68(6): 908-914.

[23] Gómez-Gardenes J,Echenique P,Moreno Y. Immunization of Real Complex Communication Networks [J]. The European Physical Journal B,2002,49(2): 259-264.

[24] Christakis N A,Fowler J H. Social Network Sensors for Early Detection of Contagious Outbreaks [J]. PLoS One,2010,5(9): e12948.

[25] HUANG Xin-li,ZOU Fu-tai,MA Fan-yuan. Targeted Local Immunization in Scale-Free Peer-to-Peer Networks [J]. Journal of Computer Science and Technology,2007,22(3): 457-468.

[26] LIU Zong-hua,HU Bambi. Epidemic Spreading in Community Networks [J]. Europhysics Letters,2005,72(2): 315-321.

[27] GAO Chao,LIU Ji-ming,ZHONG Ning. Network Immunization with Distributed Autonomy-Oriented Entities [J]. IEEE Transactions on Parallel and Distributed Systems,2011,22(7): 1222-1229.

[28] HUANG Jing,LIU Da-you,YANG Bo,et al. A Self-organization Based Divide and Conquer Algorithm for Distributed Constraint Optimization Problems [J]. Journal of Computer Research and Development,2008,45(11): 1831-1839. (黄晶,刘大有,杨博,等. 自组织分治求解分布式约束优化问题 [J]. 计算机研究与发展,2008,45(11): 1831-1839.)

[29] Bu S T,Towsley D. On Distinguishing between Internet Power Law Topology Generators [C]//Proceedings of the 21st Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM’02). New York: IEEE,2002: 638-647.

[30] Zou C C,Towsley D,GONG Wei-bo. Modeling and Simulation Study of the Propagation and Defense of Internet E-mail Worms [J]. IEEE Transaction on Dependable and Secure Computing,2007,4(2): 105-118.

[31] Dickison M,Havlin S,Stanley H E. Epidemics on Interconnected Networks [J]. Physical Review E,2012,85(6): 066109.

[32] Tanizawa T,Havlin S,Stanley H E. Robustness of Onionlike Correlated Networks against Targeted Attacks [J]. Physical Review E,2012,85(4): 046109.

[33] Parshani R,Buldyrev S V,Havlin S. Interdependent Networks: Reducing the Coupling Strength Leads to a Change from a First to Second Order Percolation Transition [J]. Physical Review Letters,2010,105(4): 048701.