一种凹形区域和简单宽边界区域间的拓扑关系表示模型

王立君,富 倩

(1. 长春工业大学 信息传播工程学院,长春 130012;2. 吉林大学 地球科学学院,长春 130061)

空间推理[1]就是运用空间理论与人工智能技术和方法对空间对象进行建模、 描述和表示,并对其空间关系进行分析和处理的过程. 它在地理信息系统(GIS)、 图形图像处理、 模式识别、 机器人导航和空间数据库等领域应用广泛[2-3]. 空间关系模型研究是空间推理的基本内容,其中大多数为拓扑关系模型研究[4-8]. 现有空间拓扑关系模型大多数针对简单对象和确定性对象,对于现实世界中普遍存在的复杂对象及不确定性对象的处理能力较弱. 本文针对二维空间中的平面区域,基于空间拓扑关系模型中经典的区域连接演算(RCC)理论,提出一种凹形区域和宽边界区域间的拓扑关系表示模型,能对复杂对象和不确定性对象中较简单情况进行有效处理.

1 凹形区域

定义1[9]取平面区域P中任意两点做连线,若连线上的任意点总在区域P中,则称P为凸形区域.

定义2[9]取平面区域P中任意两点做连线,若连线上存在某一点不在区域P中,则称P为凹形区域.

定义3[4]平面内包含区域P的最小凸形区域,称为P的凸壳,记为Pch.

定义4[4]凹形区域P的凸壳与P自身做差得到的部分,称为P的内侧,记为Pi.

如图1所示,Pi为凹形区域P的内侧,P∪Pi即为P的凸壳.

2 宽边界区域

宽边界区域[10-12]是一种用于处理不确定性对象的表示方法. 宽边界区域通常由内、 外区域组成,内区域表示宽边界一定存在的范围,外区域表示宽边界可能存在的范围. 内、 外区域之差即为宽边界,它具有一定的宽度和面积.

定义5令A为宽边界区域,由两个简单区域A1和A2组成,且满足A1⊂A2,则A1称为A的内区域,A2称为A的外区域,内、 外区域之差即为A的宽边界,记为ΔA=A2-A1.

如图2所示,A为宽边界区域,A1,A2分别为A的内、 外区域,ΔA为A的宽边界.

图1 Pi为凹形区域P的内侧Fig.1 Pi inside concave region P

图2 宽边界区域A及其各组成部分Fig.2 Broad boundary region A and its composite parts

3 凹形区域和宽边界区域的拓扑关系表示模型

3.1 空间区域划分 令X,Y分别为二维空间中的凹形区域和宽边界区域,考虑X,Y的4个组成部分,即X的内侧、X自身和Y的内、 外区域,分别记为Xi,X,Y1,Y2,如图3所示.

图3 凹形区域X和宽边界区域Y的空间划分Fig.3 Space partitions of concave region X and broad boundary region Y

令X为凹形区域,Y为简单宽边界区域,则X,Y间的拓扑关系可通过考虑各子部分间的相交情况进行描述,形式化表示为如下的4×4交集矩阵：

若每项的交集非空,则取值为1；否则,若每项的交集为空,则取值为0. 取遍所有不同的0/1组合,共有216个不同的矩阵. 考虑到现实世界中的空间对象,216个矩阵中包含了许多实际不存在的情况. 为了去掉这些实际不存在的拓扑关系,下面将给出拓扑关系生成的约束条件.

3.3 拓扑关系生成的约束条件 下面给出3个约束条件,用于得到凹形区域和简单宽边界区域间所有实际存在的拓扑关系.

约束条件1对于凹形区域X和简单宽边界区域Y的4个部分Xi,X,Y1,Y2,每部分的外部必相交,即XOO∩YOO= 1.

因为Xi,X,Y1,Y2的外部均为无限区域,而无限区域之间交集必非空,因而约束条件1合理.

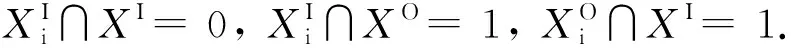
由定义4可知,凹形区域的内部与其内侧的内部必不相交,凹形区域的外部与其内侧的内部必相交,凹形区域的内部与其内侧的外部必相交,因而约束条件2合理.

由定义5可知,简单宽边界区域的内、 外区域,它们的内部必相交,内区域的内部和外区域的外部必不相交,内区域的外部和外区域的内部必相交,从而约束条件3合理.

3.4 拓扑关系表示 根据上述3个约束条件,从216个不同矩阵中删掉二维平面中实际不存在的情况,最终得到凹形区域和简单宽边界区域间的67种拓扑关系,并给出每种关系对应的示意图,如图4所示.

综上所述， 本文针对空间中一类较简单的复杂区域和不确定区域， 基于交集矩阵表示方法， 提出了一种凹形区域和简单宽边界区域间的拓扑关系表示模型， 给出了约束条件， 通过去掉二维平面中所有不可实现的情况， 最终得到实际存在的67种拓扑关系， 并给出了其拓扑关系示意图. 该模型可用于空间查询等应用领域， 在一定程度上增强了对复杂区域和不确定区域的处理能力.

[1] Cohn A G,Hazarika S M. Qualitative Spatial Representation and Reasoning: An Overview [J]. Fundamental Informatics,2001,46(1/2): 1-29.

[2] LIU Ya-bin,LIU Da-you. A Review on Spatial Reasoning and Geographic Information System [J]. Journal of Software,2000,11(12): 1598-1606. (刘亚彬,刘大有. 空间推理与地理信息系统综述 [J]. 软件学报,2000,11(12): 1598-1606.)

[3] LIU Da-you,HU He,WANG Sheng-sheng,et al. Research Progress in Spatio-Temporal Reasoning [J]. Journal of Software,2004,15(8): 1141-1149. (刘大有,胡鹤,王生生,等. 时空推理研究进展 [J]. 软件学报,2004,15(8): 1141-1149.)

[4] Clementini E,Billen R. Modeling and Computing Ternary Projective Relations between Regions [J]. IEEE Transactions on Knowledge and Data Engineering,2006,18(6): 799-814.

[5] Roussopoulos N,Faloutsos C,Sellis T. An Efficient Pictorial Database System for PSQL [J]. IEEE Transactions on Software Engineering,1988,14(5): 639-650.

[6] Cohn A G,Bennett B,Gooday J,et al. Qualitative Spatial Representation and Reasoning with the Region Connection Calculus [J]. GeoInformatica,1997,1(3): 275-316.

[7] LI San-jiang. A Complete Classification of Topological Relations Using the 9-Intersection Method [J]. International Journal of Geographical Information Science,2006,20(6): 589-610.

[8] Roy A J,Stell J G. Spatial Relations between Indeterminate Regions [J]. International Journal of Approximate Reasoning,2001,27(3): 205-234.

[9] Egenhofer M J,Vasardani M. Spatial Reasoning with a Hole [C]//Conference on Spatial Information Theory (COSIT-07). Berlin: Springer,2007: 303-320.

[10] OUYANG Ji-hong,HUO Lin-lin,LIU Da-you,et al. Extended 9-Intersection Model for Description of Topological Relations between Regions with Holes [J]. Journal of Jilin University: Engineering and Technology Edition,2009,39(6): 1595-1600. (欧阳继红,霍琳琳,刘大有,等. 能表达带洞区域拓扑关系的扩展9-交集模型 [J]. 吉林大学学报: 工学版,2009,39(6): 1595-1600.)

[11] OUYANG Ji-hong,FU Qian,LIU Da-you. A Model for Representing Topological Relations between Simple Concave Regions [J]. Journal of Jilin University: Science Edition,2007,45(3): 427-431. (欧阳继红,富倩,刘大有. 一种简单凹形区域间拓扑关系的表示模型 [J]. 吉林大学学报: 理学版,2007,45(3): 427-431.)

[12] Clementini E,DiFelice P. An Algebraic Model for Spatial Objects with Indeterminate Boundaries [C]//Geographic Objects with Indeterminate Boundaries. London: Taylor &Francis,1996: 155-169.