粗糙线性空间的性质研究*
2013-12-03李小朝
李小朝 张 巧
(1黄淮学院数学科学系;2驻马店市第十二初级中学 河南驻马店 463000)
引言
自1982年波兰学者Pawlak在文献[1]中首先提出粗糙集的概念以来,粗糙集理论在数据的决策与分析,机器学习和知识发现等领域得到广泛应用.近年来,粗糙集理论被成功地应用到各种代数系统上,得到了一系列有价值的结果.文献[2,3,4]研究了半群的粗糙群, 粗糙子群和粗糙理想等粗糙代数的性质.文献[5,6]研究了粗糙群的同态和同构的若干性质.在文献[7]中,笔者把粗糙集理论引入到李代数上,研究了李代数的粗糙子代数和粗糙理想等.文献[8,9]研究了粗糙线性空间及线性空间基于同余的上(下)近似.本文在文献[8,9]对粗糙线性空间研究的基础上,进一步研究粗糙线性空间的子空间、同态等.
本文总假设L是数域P上的线性空间,所用符合、术语和定义1,2参见文献[8,9].
1 粗糙线性空间
定义1 设A,B是线性空间L的非空子集,k为数域P中任意元素.定义A与B的和为:A+B={α+β|α∈A,β∈B};k与A的乘积为:kA={kα|α∈A}.
定义2 设W是线性空间L的子空间,对任意α,β∈L若α-β∈W,则称α与β同余,记为xRy.用R(x)表示包含x的同余类, 显然R(x)=x+W.












2 粗糙线性空间的子空间
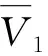

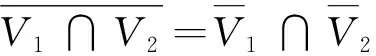
定理6 若V1,V2是粗糙线性空间V的粗糙子空间,则V1+V2也是V的粗糙子空间.
证明:由于V1,V2是粗糙线性空间V的粗糙子空间,则有V1+W,V2+W是线性空间. 由于(V1+W)+(V2+W)=V1+V2+W仍是线性空间,因此V1+V2也是V的粗糙子空间.

定理7 设粗糙线性空间V1,V2是粗糙同态的,则f(V1)也是粗糙线性空间.
证明:由定义5知结论显然.



故由定理2知f(H1)是V2的粗糙子空间.
参考文献:
[1]Zdzislaw Pawlak. Rough sets [J]. International Journal of Computer & Information Sciences,1982,11(5):341.
[2]Biswas R,Nanda S. Rough groups and rough subgroups[J]. Bull Polish Acad Sci Math,1994,42(1):251.
[3]Kuroki N. Rough ideals in semigroups[J].Information Science, 1997,100(1-4):139.
[4]Miao DQ,Han SQ,Li DG,et al. Rough group, rough subgroup and their properties[J]. Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing Lecture Notes in Computer Science,2005,364(1):104.
[5]舒兰,王德松.粗糙群同态基本定理与同构[J].计算机科学,2003,30(5专刊):32.
[6]韩素青.粗糙群的同态和同构[J].山西大学学报,2001,42(24):303.
[7]李小朝.李代数的粗糙子代数和粗糙理想[J].河南科学,2011,29(12):1406.
[8]吴明芬.线性空间上基于同余的上(下)近似[J].模糊系统与数学,2008,22(1):146.
[9]Liu WJ. Rough Linear Space[J]. Fuzzy System and Mathematics,2007,21(4):137.
