带宽极图的一个反例
2013-12-03陆锋
陆 锋
(湄洲湾职业技术学院 福建莆田 351254)
1 准备知识
笔者先给出一些本文将要用到的引理和定义.

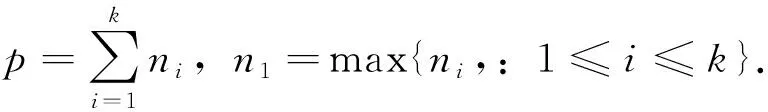

引理1.4[3]当B=p-1时,Kp是e(p,B)的唯一极图.
定义1.1[4]对于任意整数k≥1,定义一个二部图Hk=(X,Y;E):其中顶点集为X∪Y,边集为E,X={x1,x2,…,xk},Y={y1,y2,…,yk},E={xi,yj;i+j>k}.
例如:H1,H2,H3如图1所示.
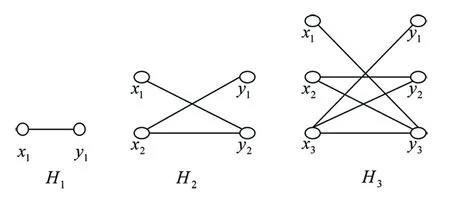
图1 H1,H2,H3极图

由引理1.5可知:
(1)B(G)=p-1成立的充要条件是G是完全图;


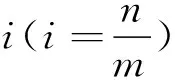
定义1.2[5]若V(G1)∩v(G2)=ø,定义G1和G2的并图G1∪G2,其顶点集为V(G1)∪V(G2),边集为E(G1)∪E(G2).
定义1.3[5]定义图的联G=G1vG2v…vGk.设图G1,G2,…,Gk个满足如下条件:
(1)V1(G)∩V2(G)∩…∩Vk(G)=ø;
(2)V(G)=V1(G)∪V2(G)∪…∪Vk(G);
(3)E(G)={E(G1)∪E(G2)∪…∪E(Gk)∪{ui,vj};u∈V(Gi),v∈(Gj),1≤i≤k,1≤j≤k,i≠j}.
例如:p3vp4如图2所示.
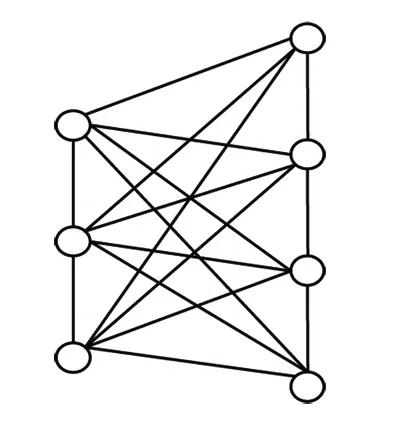
图2 p3vp4极图
2 反例

对于f(p,B)文章[1]给出如下命题:
命题2.1[1]设p=3k+r(1≤k,1≤r≤3),则





图3 命题1的反例图
为了证明图3为命题2.1的反例.首先笔者证明如下命题:
命题:对于图3的图G,B(G)=5.
证明:如图4所示图G在该标号下B(G,f)=5.于是由带宽定义有B(G)≤5.

图4 B(G)≤5的带宽极图

假设f1为G的带宽为4的任一最优标号.首先考虑G的子图K3,1,1,1.显然在f1的标号下子图K3,1,1,1的带宽为4.而实际上,此时K3,1,1,1的非同构的标号顺序只有如图5显示的两种情况(因为若5度点标号为1或者6时,在此标号下的带宽值就为5.所以在带宽为4的最优标号下K3,1,1,1中任意5度点都不可能排在首或尾,且有对称性,3个5度点只有连续排列或者中间夹杂一个3度点.


图5 K3,1,1,1的非同构的标号顺序图
进一步笔者考虑点v.观察G易知,v与K3,1,1,1的3个3度点都相连.由于在图5的标号排列下首尾都是3度点,所以可见v无论插入该标号排列的哪个位置都将造成在此标号下G的带宽超过4,这与假设矛盾.所以假设不成立,于是B(G),综上命题成立.证毕.

3 e(p,p-2)的所有极图
由e(p,B)和f(p,B)的定义可得e(p,B)≤f(p,B).笔者首先研究e(p,p-2)的极图的性质和结构.











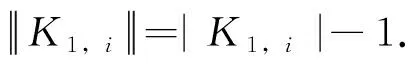
下面定理给出e(p,p-2)的所有极图的构造公式.
定理3.2 设p=3k+r(1≤k,1≤r≤3),则



证明:首先证(1).
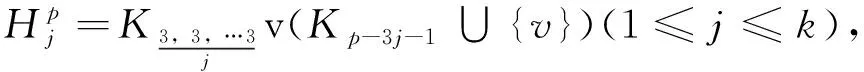
(2)与(3)同理可得,证毕.图6列出e(7,5)极图的补图的所有情况.

图6 e(7,5)极图的补图
由定理3.1笔者有如下推论:
推论1[3]当B=p-2时,设p=3k+r(1≤k,1≤r≤3),完全(k+1)-部图K3,3,…,3,r是e(p,B)的一个极图.
推论2设p=3k+r(1≤k,1≤r≤3),则
(1)当k=r=1时,f(p,p-2)=4,图K2,2是f(p,p-2)的唯一极图;



证明:由e(p,B)和f(p,B)的定义显然可得e(p,B)≤f(p,B).若e(p,B)得一个极图满足△(G)≤B,则G也是f(p,B)的一个极图.

由定理3.2以及e(p,B)和f(p,B)的关系易知(2)(3)也成立.
参考文献:
[1]Yang Aifeng,Lin Yixun. Some results on an extreml bandwidth graph problem[J].Mathematica Applicata,2003,(16)1:143.
[2]DJ Miller. The Categorical product of graphs[J].Can J Math,1968,20(4):1511.
[3]Ronald D Dutton, Robert C Brigham. On the size of graphs of a given bandwidth [J]. Discrete Mathematics,1989,76(3):191.
[4]林治勋.图带宽问题的若干刻划[J].运筹学学报,2000,19(2):1.
[5]JA Bondy,USR Murty. Graph Theory[M]. Springer Verlag,2008.26.
[6]PZ Chinn,J Chvbtalovb, AK Dewdey,et al. The bandwidth problem for graphs and matrices-a survey [J]. Journal of Graph Theory,1982,6(3):223.
