广义二次矩阵和与积线性组合的秩与零度

刘淑媛， 陈梅香， 冯晓霞， 杨忠鹏, 谢燕萍

(1. 吉林工商学院 基础部， 长春 130062； 2. 莆田学院 数学系， 福建 莆田 351100；3. 漳州师范学院 数学与信息科学系， 福建 漳州 363000； 4. 福建师范大学 数学与计算机科学学院， 福州 350007)

幂等矩阵在矩阵研究领域应用广泛, 目前已取得丰富的研究成果. 例如: Baksalary等[1]考虑幂等矩阵P,Q线性组合的可逆性， 证明了aP+bQ可逆当且仅当P+Q可逆， 其中ab(a+b)≠0,a,b∈. 文献[2-3]在相同的约束条件下， 证明了幂等矩阵线性组合的秩及零度的不变性. 文献[4]推广了文献[3,5]的结果: 对于幂等矩阵P,Q, 证明了

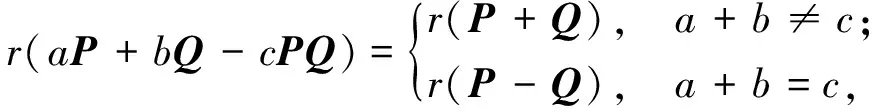
(1)

其中a,b,c∈， 且ab≠0.

设A∈Cn×n， 若存在d,e∈, 使得(A-dI)(A-eI)=0, 则称A为(由d,e确定的)二次矩阵[6-7]. 二次矩阵集合记为

(2)

其中Ωn(I;d,e)={A∈Cn×n: (A-dI)(A-eI)=0}. 文献[8]给出了二次矩阵的和与积的线性组合的秩不变性结论: 设A,B∈Ωn(I;d,e)， 复数d≠e,a≠0,b≠0, 则

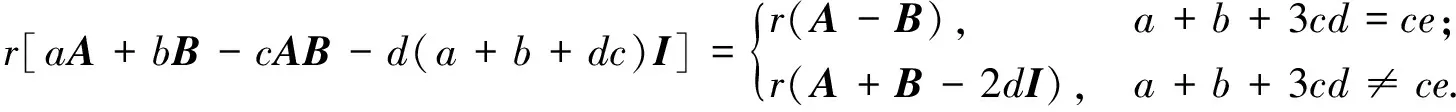
文献[9]给出了广义二次矩阵的概念: 设A∈Cn×n， 如果存在d,e∈及幂等矩阵P, 使得

AP=PA=A, (A-dP)(A-eP)=0,

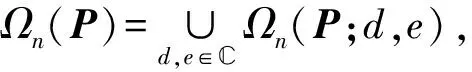
Ωn(P;d,e)={A∈Cn×n: (A-dP)(A-eP)=0,AP=PA=A}.

本文讨论广义二次矩阵和与积线性组合的秩与其组合系数选择无关的问题， 推广并改进了已有的相关结果.

引理1[12]设A∈Cn×n， 如果存在d,e∈及幂等矩阵P, 使得AP=PA=A， 则当d≠e时， 有A∈Ωn(P;d,e)⟺是幂等的.

定理1给定幂等矩阵P,Q, 设A∈Ωn(P;dA,eA),B∈Ωn(Q;dB,eB) ， 其中:dA≠eA;dB≠eB. 对于a,b,c∈， 如果ab(a-cdB)(b-cdA)≠0， 则:

r[(aA+bB-cAB)-(adAP+bdBQ)-c(dBA(P-Q)+dA(Q-P)B-dAdB(P+Q-PQ))]=

(3)

null[(aA+bB-cAB)-(adAP+bdBQ)-c(dBA(P-Q)+dA(Q-P)B-dAdB(P+Q-PQ))]=

(4)

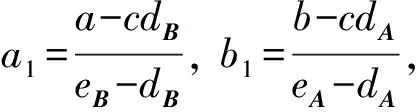
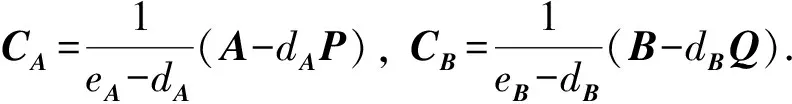
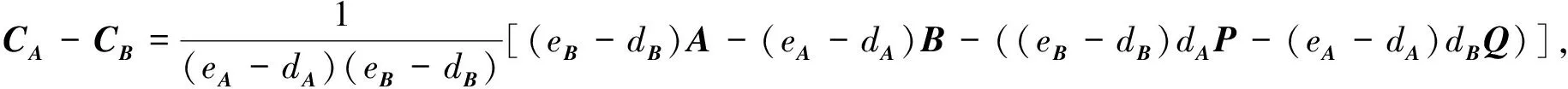
(7)

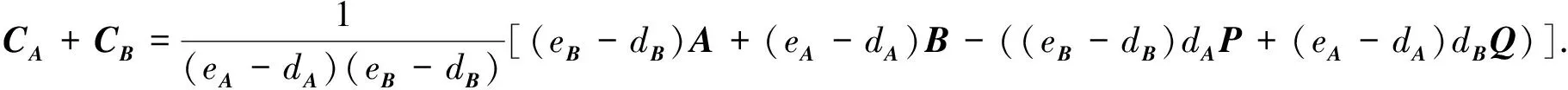
(8)

当a(eA-dA)+b(eB-dB)=c(eAeB-dAdB)时， 由式(1)，(5)～(7)可得

当a(eA-dA)+b(eB-dB)≠c(eAeB-dAdB)时， 由式(1)，(5)，(6)，(8)可得

即式(3)成立. 又因为null(A)=n-r(A), 进而可得式(4).

当c=0时， 由式(3)可得文献[12]中定理2.

定理2设P是幂等矩阵,A,B∈Ωn(P;1,e), 其中e≠1, 则

r[aA+bB-(a+b)P]=r(A+B-2P)，

其中a,b∈, 使得ab(a+b)≠ 0.

当P=I时， 定理2推广了文献[13]的定理2.2和定理2.6. 取P=Q=I， 则由定理1可得如下与文献[8]类似的结果:

推论1设A,B∈Ωn(I;d,e)， 其中d≠e, 如果a,b,c∈,ab(a-cd)(b-cd)≠0， 则

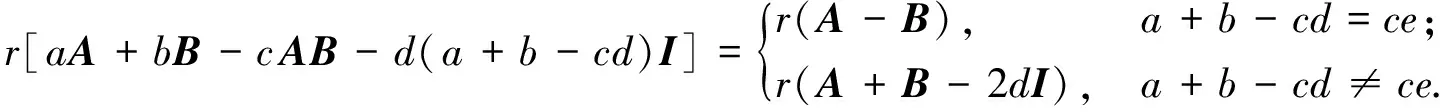
[1] Baksalary J K, Baksalary O M. Nonsingularity of Linear Combinations of Idempotent Matrices [J]. Linear Algebra Appl, 2004， 388(1)： 25-29.

[2] Koliha J J, Rakocevic V. The Nullity and Rank of Linear Combinations of Idempotent Matrices [J]. Linear Algebra Appl, 2006， 418(1)： 11-14.

[3] TIAN Yong-ge, Styan G P H. Rank Equalities for Idempotent Matrices with Applications [J]. J Comp Appl Math, 2006， 191(1)： 77-97.

[4] ZUO Ke-zheng. The Nullity and Rank of Combinations of Idempotent Matrices [J]. J Math, 2008, 28(6): 619-622.

[5] TIAN Yong-ge, Styan G P H. Rank Equalities for Idempotent and Involutory Matrices [J]. Linear Algebra Appl, 2001， 335： 101-117.

[6] Aleksiejczyk M, Smoktunowicz A. On Properties of Quadratic Matrices [J]. Math Pannon, 2000， 11(2)： 239-248.

[7] GAU Hwa-long, WANG Chih-jen, WONG Ngai-ching. Invertibility and Fredholmness of Linear Combinations of Quadratic,k-Potent and Nilpotent Operators [J]. Operators and Matrices， 2008， 2(2)： 193-199.

[8] XIE Tao. Invertibility of Combinations of Two Quadratic Matrices [J] . Journal of Baoji University of Arts and Science: Natural Science, 2010, 30(3): 18-21. (谢涛. 两个二次矩阵组合的可逆性 [J]. 宝鸡文理学院学报: 自然科学版, 2010, 30(3): 18-21.)

[9] Farebrother R W, Trenkler G. On Generalized Quadratic Matrices [J]. Linear Algebra Appl, 2005, 410: 244-253.

[10] DENG Chun-yuan. On Properties of Generalized Quadratic Operators [J]. Linear Algebra Appl, 2010, 432(4): 847-856.

[11] YANG Zhong-peng, FENG Xiao-xia, CHEN Mei-xiang, et al. Fredholm Stability Results for Linear Combinations ofm-Potent Operators [J]. Operators and Matrices, 2012, 6(1): 193-199.

[12] LIU Shu-yuan, YANG Zhong-peng, XIE Yan-ping. Rank and Nullity for Linear Combinations of Generalized Quadratic Matrices [J]. Journal of Jilin University: Science Edition, 2011, 49(6)： 993-996. (刘淑媛， 杨忠鹏， 谢燕萍. 广义二次矩阵线性组合的秩与零度 [J]. 吉林大学学报: 理学版， 2011, 49(6)： 993-996.)

[13] ZHANG Jin-hui, WANG Hai-ming, YANG Zhong-peng, et al. Invariance of Rank for Linear Combinations of Scalar-Involutory Matrices [J]. J Math Study, 2010， 43(1)： 98-103. (张金辉, 王海明， 杨忠鹏， 等. 数量对合矩阵的线性组合的秩的不变性 [J]. 数学研究, 2010， 43(1)： 98-103.)