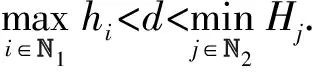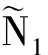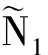局部α-双对角占优矩阵及其应用

邰志艳, 李庆春

(1. 吉林医药学院 数学教研室, 吉林 吉林 132013； 2. 北华大学 数学学院, 吉林 吉林 132013)

广义严格对角占优矩阵在计算数学、 数学物理、 优化理论等领域应用广泛, 但其实际判别却很困难[1-16]. 本文利用局部α-双对角占优矩阵理论给出几种新的广义严格对角占优矩阵的判别方法, 推广和改进了文献[2]的主要结果.

1 定义及引理

定义1设A=(aij)∈Mn(C), 若|aii|≥ri(A), ∀i∈N, 则称A为对角占优矩阵, 记为A∈D0. 若|aii|>ri(A), ∀i∈N, 则称A为严格对角占优矩阵, 记为A∈D. 若存在正对角矩阵X, 使得AX∈D, 则称A为广义严格对角占优矩阵, 记为A∈D*.

定义2设A=(aij)∈Mn(C), N1∩N2=Ø, N1⊕N2=N, 若∀i∈N1及∀j∈N2, 存在α∈(0,1], 使得

(1)

且

Ø,

则称A为局部α-双对角占优矩阵, 记为A∈LD0(α).

若式(1)中均为严格不等式, 则称A为局部α-双严格对角占优矩阵, 记为A∈LD(α). 若式(1)中至少有一个为严格不等式, 且A为不可约矩阵, 则称A为不可约局部α-双对角占优矩阵, 记为A∈ILD0(α).

引理1[1]设A=(aij)∈Mn(C), 若存在α∈(0,1], 使得|aii|>αri(A)+(1-α)Ci(A), 则A∈D*.

引理2[1]设A=(aij)∈Mn(C)是不可约矩阵, 若存在α∈(0,1], 使得∀i∈N, 有|aii|≥αri(A)+(1-α)Ci(A), 且

J={j∈N: |ajj|>αrj(A)+(1-α)Cj(A)}≠Ø,

则A∈D*.

2 主要结果

定理1设A=(aij)∈Mn(C), 若A是局部α-双严格对角占优矩阵, 则A∈D*.

证明： 由Ω+≠Ø知,Ω+=N, 即∀i∈N, 均有

记

∀i∈N1,

(2)

(3)

X=diag(di:di=d,i∈N1;di=1,i∈N2),

则矩阵AX=(bij)满足当i∈N1时, 由d>hi及式(2)有

从而

(4)

将式(4)两端分别乘以α, 得

|bii|>αri(B)+(1-α)Ci(B).

当j∈N2时, 由d

即

(5)

将式(5)两端分别乘以α, 得

|bjj|>αrj(B)+(1-α)Cj(B).

(6)

综上知B满足引理1的条件, 从而B∈D*, 进而A=BX-1∈D*.

定理2设A=(aij)∈Mn(C), 若A是不可约局部α-双对角占优矩阵, 则A∈D*.

证明： 记

由A是不可约局部α-双对角占优矩阵知,J*≠Ø, 且Ω+≠Ø. 不难验证∀i∈N, 均有

若存在i∈N1, 满足

(7)

其中Aii(i=1,2)是以 Ni(i=1,2)中的元素为行、 列足码的A的主子阵, 从而由式(7)知A是可约矩阵, 与已知矛盾.

若存在j∈N2, 满足

则由A是不可约局部α-双对角占优矩阵知, 存在i∈N1, 使得

构造正对角矩阵D=diag(di:di=d,i∈N1;di=1,i∈N2), 则矩阵B=AD=(bjj)n×n, 满足当i∈N1时, 由d≥hi及hi所设, 仿定理1的证明, 得

|bii|≥αri(B)+(1-α)Ci(B).

当j∈N2时, 由d≤Hj及Hj所设, 仿定理1的证明, 得

|bjj|≥αrj(B)+(1-α)Cj(B).

再由J*≠Ø知, 存在j∈N, 使得式(6)成立.

综上知,B满足引理2的条件, 从而B∈D*, 进而A=BD-1∈D*.

定理3设A=(aij)∈Mn(C),aii≠0(i∈N), N=N1+N2, N1∩N2=Ø, 若∀i∈N1,j∈N2, 则存在α∈(0,1], 使得

且J*≠Ø(J*同定理2); 若∀i∈NJ*, 有非零元素链aii1,ai1i2,…,aip j, 使得j∈J*, 则A∈D*.

证明： 若A是不可约矩阵, 则由定理2知,A∈D*. 若A是可约矩阵, 则存在置换矩阵P, 使得

(8)

其中Aii(1≤i≤k)是ni阶不可约矩阵.

再由J*≠Ø及∀i∈NJ*有非零元素链aii1,ai1i2,…,aip j, 使得j∈J*和式(8)知,

由Aii不可约及定理2知,Aii∈D*.

同时, 由J*≠Ø知, 存在i∈Nii, 使得

再由A是不可约矩阵及引理2知,Aii∈D*.

综上知, ∀i∈{1,2,…,k}, 有Aii∈D*. 由式(8)知PAPT∈D*, 又由P是置换矩阵知,A∈D*.

综上所述, 本文给出了局部α-双对角占优矩阵的概念, 并应用局部α-双对角占优矩阵的理论给出了广义严格对角占优矩阵的几个新的充分条件, 推广和改进了文献[2]的主要定理, 拓展了广义严格对角占优矩阵的判定准则.

[1] ZHANG Yue-lang, MO Hong-min, LIU Jian-zhou.α-Diagonally Dominant and Criteria for Generalized Strictly Diagonally Dominant Matrices [J]. Numerical Mathematics A Journal of Chinese Universities, 2009, 31(2): 119-128. (张月朗, 莫宏敏, 刘建州.α-对角占优与广义严格对角占优矩阵的判定 [J]. 高等学校计算数学学报, 2009, 31(2)： 119-128.)

[2] WANG Xin-cun, GUAN Yu-jing. Local Double Diagonally Dominant Matrices and Its Application [J]. Journal of Jilin University: Science Edition, 2010, 48(5)： 401-405. (王信存, 关玉景. 局部双对角占优矩阵及其应用 [J]. 吉林大学学报: 理学版, 2010, 48(5)： 401-405.)

[3] GUO Li. Criteria for Nonsingular H-Matrices [J]. Journal of Jilin University: Science Edition, 2010, 48(2)： 226-228. (郭丽. 非奇异H-矩阵的判定 [J]. 吉林大学学报: 理学版, 2010, 48(2)： 226-228.)

[4] TAI Zhi-yan, LI Qing-chun. New Criteria for Generalized Strictly Diagonally Dominant Matrices [J]. Journal of Jilin University: Science Edition, 2011, 49(2)： 218-222. (邰志艳, 李庆春. 广义严格对角占优的新判定条件 [J]. 吉林大学学报: 理学版, 2011, 49(2)： 218-222.)

[5] Varga R S. On Recurring Theorems on Diagonal Dominace [J]. Linear Algebra and Its Applications, 1976, 13(1/2)： 1-9.

[6] ZHAO Liang-dong, XU Zhong, LU Quan. Improved Determinate Conditions for the Nonsingular H-Matrix [J]. Chinese Journal of Engineering Mathematics, 2010, 27(6)： 1015-1020. (赵良东, 徐仲, 陆全. 改进的非奇H矩阵的判定条件 [J]. 工程数学学报, 2010, 27(6)： 1015-1020.)

[7] XIE Qing-ming. A Note on the Practical Criteria for H-Matrices [J]. Acta Mathematicae Applicatae Sinica, 2006, 29(6)： 1080-1084. (谢清明. 关于H-矩阵的实用判定的注记 [J]. 应用数学学报, 2006, 29(6)： 1080-1084.)

[8] HAN Tao, LU Quan, XU Zhong, et al. Some New Criteria for Nonsingular H-Matrices [J]. Chinese Journal of Engineering Mathematics, 2011, 28(4)： 498-504. (韩涛, 陆全, 徐仲, 等. 一组非奇异H-矩阵的新判据 [J]. 工程数学学报, 2011, 28(4)： 498-504.)

[9] Berman A, Plemmons R J. Nonnegative Matrices in the Mathematical Sciences [M]. New York: Academic, 1979.

[10] GAN Tai-bin, HUANG Ting-zhu. Simple Criteria for Nonsingular H-Matrices [J]. Linear Algebra Appl, 2003, 374(15): 317-326.

[11] Horn R A, Johnson C R. Mathix Analysis [M]. New York: Cambridge University Press, 1985: 349-350.

[12] Cvetkovic L, Kostic V, Varga R S. A New Geršgorin-Type Eigenvalue Inclusion Set [J]. Electronic Transactions on Numerical Analysis, 2004, 18: 73-80.

[13] Varga R S. Matrix Iterative Analysis [M]. 2nd ed. Berlin: Springer-Verlag, 2000: 87-93.

[14] LI Min, SUN Yu-xiang. Practical Criteria for H-Matrices [J]. Appl Math Comp, 2009, 211(2): 427-433.

[15] SUN Yu-xiang. Sufficient Conditions for Generalized Diagonally Dominant Matrices [J]. Numerical Mathematics A Journal of Chinese Universities, 1997(3): 216-223. (孙玉祥. 广义对角占优矩阵的充分条件 [J]. 高等学校计算数学学报, 1997(3): 216-223.)

[16] LI Ji-cheng, ZHANG Wen-xiu. Criteria for H-Matrices [J]. Numerical Mathematics A Journal of Chinese Universities, 1999(3): 264-268. (李继成, 张文修. H-矩阵的判定 [J]. 高等学校计算数学学报, 1999(3): 264-268.)