一种基于显著性的多尺度图像融合模型

李 蕴 奇

(吉林省经济信息中心, 长春 130061)

图像融合是指将多幅由不同传感器或在不同环境下获得的同一场景图像合成一张图像, 并使合成后的图像信息更丰富, 更适合后期处理[1]. 该技术目前已应用于医疗辅助诊断和治疗、 遥感图像、 机器人视觉等领域. 优异的融合算法应满足3个条件[2]： 1) 在融合图像中应保留所有与输入图像相关的信息； 2) 不能引入影响肉眼观察或影响下一步计算机处理的不一致性； 3) 具有平移不变性和旋转不变性.

目前的融合算法按融合层次可归结为像素级、 特征级和决策级3类[3]. 像素级的图像融合方法又可分为空域类和频域类两种[2], 空域类包括最大值法、 最小值法和PCA法等; 而频域类相对于空域类过程更复杂, 其过程分为3个阶段： 将图像融合空域变换到频域, 融合算子作用于频域参数, 频域再转换至空域. 频域类包括： 塔式分解法、 Fourier变换法和小波变换法等. 这些算法的不同之处在于频域与空域的变换方式不同. 频域类算法尽管算法繁琐, 时间开销大, 但它使融合效果得到极大提高. 而产生这种优越性的原因为: 在频域内, 可将图像按频率分解, 使得高频信息(如形状、 纹理等)与低频信息(如背景等平滑部分)分开, 融合算子可视具体融合参数进行选取, 针对性更强. 特征级融合类指融合算子运行在特征级[4], 一般过程为： 先对图像分割, 再提取区域特征信息, 最后进行特征融合. 决策及图像融合的一般步骤为图像分割、 提取区域特征信息, 再建立对同一目标的判别, 最后进行决策级融合. 本文采用在像素级别下频域内的融合模型, 在不引入额外信息的前提下将重要信息导入融合图像. 同时, 基于图像显著性信息最大化选取融合算子.

1 轮廓波分解与重构

多尺度信号分解方法----轮廓波变换(contourlet transform)[5]的信号分解是在离散域内通过滤波器组实现的. 该方法可分解出任意多的方向信息, 而方向性对于有效的图像表示至关重要. 轮廓波变换由于能较完整地获取信号的几何结构, 所以是一种多分辨分析的、 局部的并具有方向性的表示方法.

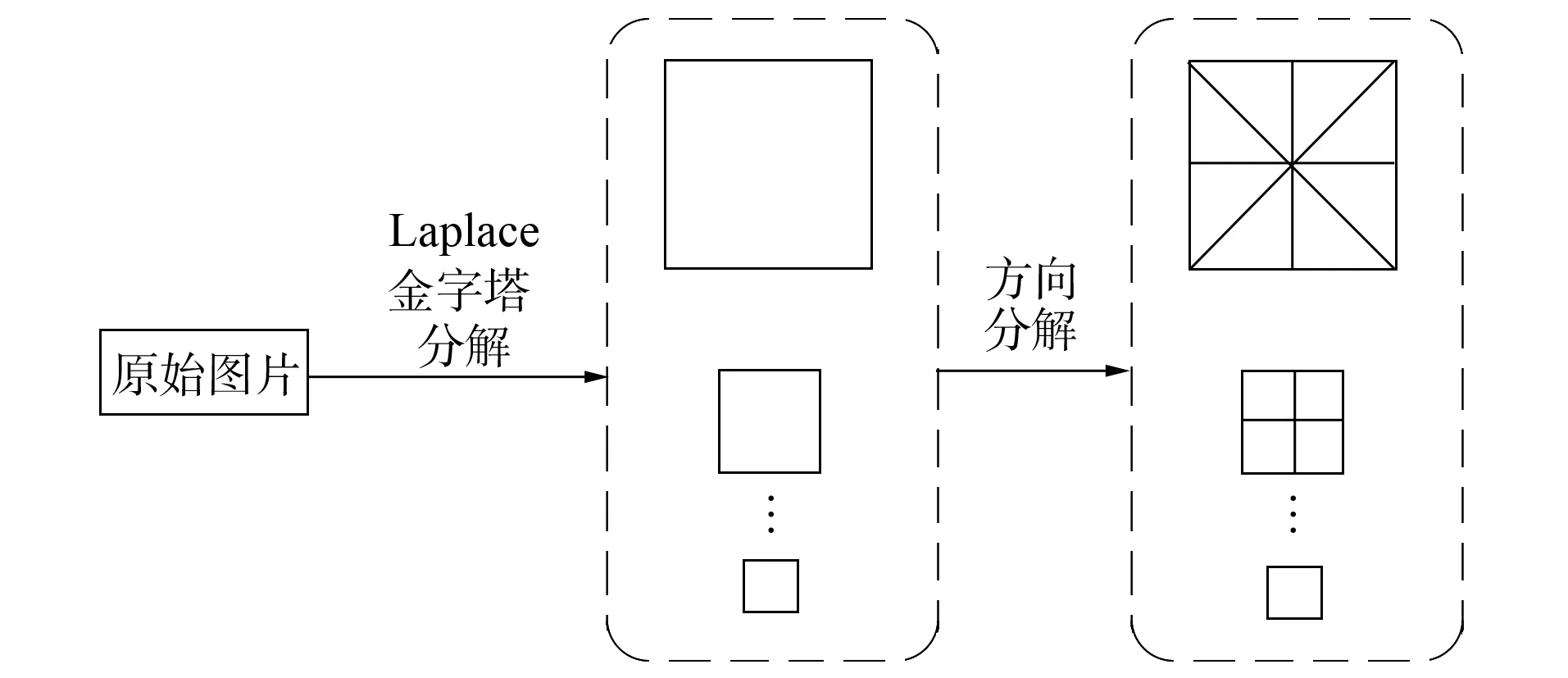
图1 轮廓波变换Fig.1 Contourlet transform

轮廓波变换可通过多尺度分解和方向分解两步完成, 如图1所示. 轮廓波变换将多尺度性和多方向性有机结合. 在第一阶段的Laplace滤波过程中, 主要寻找图像中的奇异点, 使图像中的能量主要集中于奇异点上[6]. 而在图像处理过程中, 本文更关注图像的边缘纹理信息, 而不是奇异点. 因此, 需要有效地刻画出奇异点连成的曲线. 轮廓波变换第二阶段中, 方向滤波器在Laplace分解层上进一步滤波, 使图像的能量集中于奇异线段[7]. 图像经轮廓波变换后, 可表示为一个由带有不同分解尺度和方向信息的子图组成的集合.

2 模型框架

本文模型可分为： 图像Contourlet变换、 显著性计算、 参数融合和逆变换4个阶段, 如图2所示.

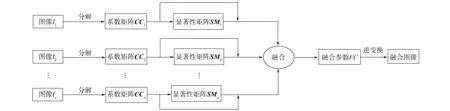
图2 模型框架Fig.2 Model framework

n(n>1)个输入图像记为I1,I2,…,In, 模型的计算过程如下：

1) 对于任意一幅原图像, 利用轮廓波变换将其分解为高频子带和低频子带, 并将每i幅原图像对应的子带集合记为CCi;

2) 计算CCi内子带中各处的显著性, 并记为集合SMi;

3) 利用显著性矩阵, 为高频子带和低频子带分别选取融合系数, 并记为集合FC;

4) 利用轮廓波逆变换获取最终融合图像.

2.1 显著性计算

本文基于谱冗余理论(spectral residual)[8]进行显著性计算. 信息可分为冗余部分和变化部分, 人们的视觉对变化部分更敏感. 视觉系统的一个基本原则是抑制对频繁出现的特征响应, 同时对非常规的特征保持敏感, 从而可将图像分为如下两部分:

H(img)=H(Innovation)+H(prior Konwledge).

设输入图像为I(x), 则根据谱冗余理论, 计算步骤如下：

1) 对图像进行Fourier变换, 并求出振幅谱A(f)和相位谱P(f):A(f)=R(F(I)),P(f)=I(F(I));

2) 计算图像log振幅谱:L(f)=log(A(f));

3) 计算冗余谱:R(f)=L(f)-hn×L(f), 其中h是一个n×n均值滤波的卷积核;

4) 获得图像显著性区域:S(I)=g(x)×F-1[exp(R(f)+P(f)]2, 其中g(x)为高斯核函数.

最终s(x)记为图像I(x)对应的显著性矩阵.

2.2 融合规则

若n(n>1)个输入图像记为I1,I2,…,In, 经轮廓波变换后, 任意一幅输入图像的第m层包含N(m)个子图, 则第i幅输入图像可表示为{CCi(j,k)|i=1,2,…,n;j=1,2,…,L;k=1,2,…,N(j)}, 其中M表示轮廓波变换中Laplace分解层数. 同理任意一幅输入图像CCi对应的显著性矩阵可表示为集合: {SMi(j,k)|i=1,2,…,n;j=1,2,…,L;k=1,2,…,N(j)}. 融合参数可表示为{FCi(j,k)|i=1,2,…,n;j=1,2,…,L;k=1,2,…,N(j)}. 于是, 可定义融合规则为

其中:x和y为图像中的横、 纵坐标;αi(j,k,x,y)为各图像的权重, 计算公式为

其中SM(j,k,x,y)表示所有分解层为j、 排在k位的子图在坐标为(x,y)处的显著性集合.

该融合规则的意义在于显著性大的像素一般在人类视觉所关注的区域出现, 而融合的目的是将输入图像中这些能引起视觉感应的信息融入到融合图像中.

3 实验与讨论

3.1 客观评价指标

本文验证融合模型有效性时使用两项客观评估指标, 从多角度比较本文算法与其他融合算法的性能.

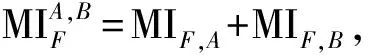
2) 文献[8]提出一种基于边缘的图像融合客观评价指标QAB/F, 该评价指标度量了融合图像的边缘完整性, 计算公式为

其中:QAF(n,m)和QBF(n,m)分别表示融合图像F与输入图像A,B之间在(m,n)处的相似性;ωA(n,m)和ωB(n,m)分别表示输入图像A,B在(m,n)处的权重.

3.2 实 验

本文选取一组通用的融合图像, 并选取小波变换图像融合法作为比较对象, 如图3所示. 输入图像A和B包含相同的目标, 二者的区别在于图像A的焦点位于右侧, 图像B的焦点位于左侧. 将两者融合成一幅图像, 有利于提高图像的清晰度, 弱化原始图像中模糊的信息. 与本文模型作比较的算法为梯度金字塔变换法、 形态学金字塔法和离散小波变换法, 这些方法在图像融合领域应用广泛, 并取得了较好的效果. 实验中, 利用梯度金字塔变换法、 形态学金字塔法和离散小波变换法进行图像融合时, 采用3层分解结构, 高频部分的融合规则为绝对值最大法, 低频部分的融合规则为均值法.

图3(F)是本文模型得到的融合结果, 与图3(C)～(E)相比, 亮度与两幅输入图像更接近, 表明在保留输入图像信息方面更优秀, 客观评价指标列于表1.

图3 输入图像与融合图像Fig.3 Source images and fused images

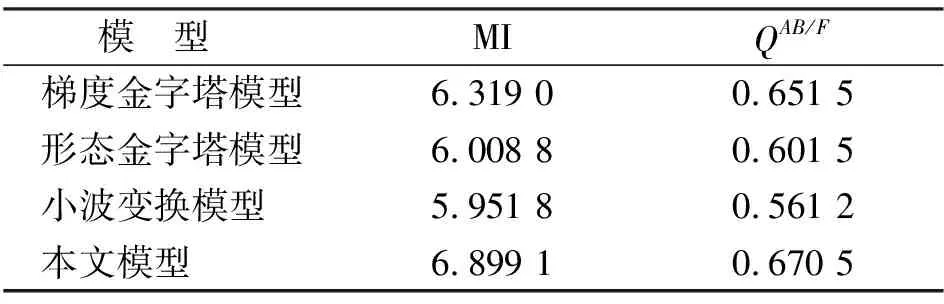
表1 客观指标评价结果

两项客观指标越大, 表明融合效果越好. 由表1可见, 本文模型更有效. 轮廓波变换能有效捕捉图像的边缘信息, 而基于谱冗余的显著信息检测能保证有用信息尽可能多的被保存到融合图像中.

综上所述, 本文提出了一种新的基于显著性的图像融合算法. 该算法首先对输入图像进行轮廓波分解, 使每幅输入图像产生一组不同分辨率的含有方向信息的子图序列； 再分别在每层子图像序列上计算局部显著性, 并根据显著性大小选取相应的融合参数； 最后进行轮廓波逆变换, 得到融合图像. 轮廓波变换的使用保证了图像信息的有效分解及边缘信息的充分采集, 基于显著性的融合策略则有利于将输入图像中的重要信息保存到最终融合图像中.

[1] LI Shu-tao, YANG Bin, HU Jing-wen. Performance Comparison of Different Multi-resolution Transforms for Image Fusion [J]. Information Fusion, 2011, 12(2): 74-84.

[2] Citardi Martin J, Batra Pete S. CT-MR Image Fusion for the Management of Skull Base Lesions [J]. Otolaryngol Head Neck Surg, 2006, 134(5): 868-876.

[3] TU Te-ming, SU Shun-chi, SHYU Hsuen-chyun, et al. A New Look at IHS-Like Image Fusion Methods [J]. Information Fusion, 2001, 2(3): 177-186.

[4] Rockinger Oliver, Fechner Thomas, Daimler Benz Ag. Pixel-Level Image Fusion: The Case of Image Sequences [C]//Proc SPIE. Bellingham: SPIE, 1998: 378-388.

[5] YANG Bo, JING Zhong-liang, ZHAO Hai-tao. Review of Pixel-Level Image Fusion [J]. Journal of Shanghai Jiaotong University: Science, 2010, 15(1): 6-12.

[6] Bender Edward J, Reese Colin E, Wal Gooitzen S. Comparison of Additive Image Fusion vs Feature-Level Image Fusion Techniques for Enhanced Night Driving [C]//Proceedings of SPIE. Bellingham: SPIE, 2003: 140.

[7] Do Minh N, Vetterli Martin. The Contourlets Transform: An Efficient Directional Multiresolution Image Representation [J]. IEEE Transactions on Imege Processing, 2005, 14: 357-360.

[8] Burt P, Adelson E. The Laplacian Pyramid as a Compact Image Code [J]. IEEE Transactions on Communications, 1983, 31(4): 532-540.

[9] Bamberger R H, Smith M J T. A Filter Bank for the Directional Decomposition of Images: Theory and Design [J]. IEEE Transactions on Signal Processing, 1992, 40(4): 882-893.