计算分岔规范型和普适开折的同调方法

彭国俊,陈潮填

(广东技术师范学院 计算机科学学院,广州 510665)

0 引 言

考虑如下向量场：

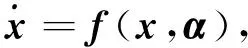
(1)

其中：x∈n,n≥2;α∈2;f:n×2→n充分光滑.向量场(1)在变换x→-x下保持不变,当α=α*时有平衡点x=0,f的Jacobi矩阵J在(x,α)=(0,α*)处非零并且有二重零特征值.文献[1-4]给出了向量场(1)的规范型和普适开折如下：

其中：当n=2时,ω=x；当n>2时,ω为限制在分岔中心流形上的状态变量.关于式(3)的分岔结构,可参考文献[5-6].一般的参数向量场(1)可约化为规范型(2),必须要求分岔是非退化的,而进一步可约化为普适开折(3)并且遍历其所有分岔结构,还要求分岔是横截的.目前,对于非对称情形的规范型已有一些显式计算结果[7-10],而对于对称情形的规范型尤其是普适开折的显式计算还未见文献报道.

为计算方便及显式地检验非退化条件,本文采用如下规范型和普适开折：

容易验证,采用如下线性坐标和时间变换：

1 规范型的计算公式

当考虑规范型时,分岔参数取临界参数值,即α=α*.由向量场(1)的对称性,可将其展开为如下形式：

(6)

定理1设向量场(1)相应于double-zero分岔的规范型为式(4),则其系数计算公式如下：

其中：qi和pi(i=1,2)分别是矩阵A和AT的广义特征向量,且满足：

Aq1=0,Aq2=q1,ATp2=0,ATp1=p2,

(9)

(10)

证明：假设此临界情形时的中心流形如下：

x=H(ω),H:2→n.

(11)

将式(11)代入式(6),根据临界中心流形的不变性可得如下同调方程：

(12)

由向量场(1)的对称性,H可以表示为如下形式：

(13)

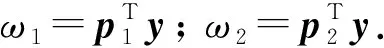
于是可得式(8).证毕.

若进一步有c30c21≠0,则对应的double-zero分岔是非退化的,即余维2的.

2 普适开折的计算公式

此时,参数α在临界值α*附近扰动.引入Δ=α-α*,由向量场(1)的对称性,将其展开为如下形式：

(16)

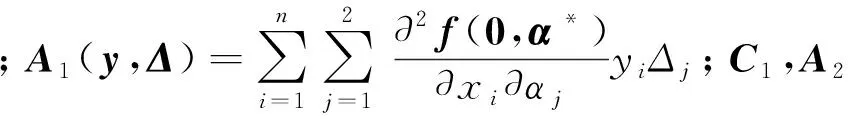
定理2设向量场(1)相应的double-zero分岔是非退化的,且具有普适开折(5).将原始参数与开折参数间的关系表示为η=V-1(Δ),并进一步采用如下平方逼近：

(17)

则线性项系数a和b由如下线性代数方程的解唯一给出：

二次项系数c,d和e由如下线性代数方程的解唯一给出：

其中hijkl(i+j=1,k+l=1)是如下奇异线性代数方程的任意解：

证明：假设参数依赖的中心流形如下：

x=H(ω,η),H:2×2→n.

(30)

将式(30)代入式(16),根据此时参数依赖中心流形的不变性,可得如下同调方程：

由向量场(1)的对称性,H可以表示为如下形式：

(32)

根据Fredholm择一性定理,上述奇异线性方程都是可解的.

(43)

(44)

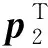
将方程(48)～(50)分别代入式(45)～(47),并消除h10kl(k+l=2),即得方程(25)～(27).于是确定了参数变换Δ=V(η),从而可求得普适开折参数η=V-1(Δ).分岔的横截性条件为

如果向量场(1)的double-zero分岔是非退化和横截的,则当分岔参数α在α*附近扰动时,普适开折(5)对不同的c30(Δ)和c21(Δ),其分岔图和相图的拓扑结构都与c30=c30(0)和c21=c21(0)时相同.

3 应用实例

考虑如下改变的van der Pol振子[7]：

(51)

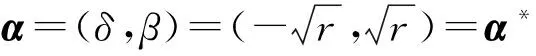
其中：s和t为任意非零实数.多线性函数C,A1,C1和A2按下式计算：

C1=A2=0.

由式(7),(8),立即可得规范型系数

因此,当m≠-n,m+n≠r(m-n)时,分岔是非退化的.扰动参数如下：

横截性满足,因为

因此,当m≠-n,m+n≠r(m-n)时,δ和β可以作为分岔参数,使系统(51)产生完整的double-zero分岔.取(m,n,r)=(-2,-1,1),根据文献[6],对应的分岔为异宿情形,计算可得如图1所示的分岔曲线：

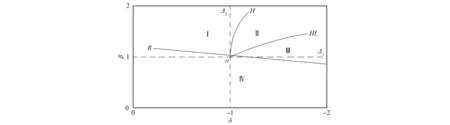
图1 系统(51)在(δ,β,m,n,r)=(-1,1,-2,-1,1)附近以(δ,β)为分岔参数的分岔曲线Fig.1 Bifurcation curves of system (51) at (δ,β,m,n,r)=(-1,1,-2,-1,1) with bifurcation parameter (δ,β)

[1] Khorozov E I.Versal Deformations of Equivariant Vector Fields in the Case of Symmetry of Order 2 and 3 [J].Transactions of Petrovski Seminar,1979,5(1)：163-192.

[2] Carr J,Sanders J A,Van,Gils S A.Nonresonant Bifurcations with Symmetry [J].SIAM Journal on Mathematical Analysis,1987,18(3)：579-591.

[3] Knobloch E,Proctor M R E.Nonlinear Periodic Convection in Double-Diffusive Systems [J].Journal of Fluid Mechanics,1981,108(1)：291-316.

[4] 唐云.对称性分岔理论基础 [M].北京：科学出版社,2000.

[5] Guckenheimer J,Holmes P J.Nonlinear Oscillations,Dynamical Systems,and Bifurcations of Vector Fields [M].New York：Springer,1983.

[6] Chow S N,LI Cheng-zhi,WANG Duo.Normal Forms and Bifurcation of Planar Vector Fields [M].Cambridge：Cambridge University Press,1994.

[7] Kuznetsov Y A.Practical Computation of Normal Forms on Center Manifolds at Degenerate Bogdanov-Takens Bifurcations [J].International Journal of Bifurcation and Chaos,2005,15(11)：3535-3546.

[8] PENG Guo-jun,JIANG Yao-lin,LI Chang-pin.Bifurcations of a Holling-Type Ⅱ Predator-Prey System with Constant Rate Harvesting [J].International Journal of Bifurcation and Chaos,2009,19(8)：2499-2514.

[9] Carrillo F A,Verduzco F,Delgado J.Analysis of the Takens-Bogdanov Bifrucation on am-Parameterized Vector Fields [J].International Journal of Bifurcation and Chaos,2010,20(4)：995-1005.

[10] PENG Guo-jun,JIANG Yao-lin.Practical Computation of Normal Forms of the Bogdanov-Takens Bifurcation [J].Nonlinear Dynamics,2011,66(1/2)：99-132.