镧系氮化物弹性性质与光学性质的第一性原理计算

杨晓翠,赵衍辉,刘 芳,罗香怡,肖俊平

(1.白城师范学院 物理学院,吉林 白城 137000;2.吉林大学 超硬材料国家重点实验室,长春 130012)

镧系氮化物具有较好的导电性、高硬度和高熔点等优异的物理化学性质,在反应堆的保护材料、防火材料、光学玻璃和陶瓷材料等领域应用广泛,目前已有许多研究结果.如Vaitheeswaran等[1]从理论上计算了LaN的结构相变和超导电性;Ciftci等[2]利用第一性原理计算了LaN的结构稳定性、弹性和热动力学性质;Ghezail等[3]利用第一性原理研究了LaN的结构和电子性质;Svane等[4]从理论上研究了高压下Ce磷族化合物(CeX,X=N,P,As,Sb,Bi)的电子结构;Lee等[5]在MgO(001)面外延生长出CeN膜;Kanchana等[6]利用从头算方法研究了CeN的电子结构、结构稳定性和晶格动力学性质;Olsen等[7]从理论和实验上研究了CeN的结构稳定性和压缩率;Petukhov[8]利用第一性原理计算了GdN的电子能带结构、体模量和凝聚能等物理性质;Larson等[9]理论计算了GdX(X=N,P,As,Sb,Bi)的电子结构和磁学性质;Leuenberger等[10]测量了GdN薄膜的电子和磁学性质;Aerts等[11]研究了LnN(CeN～YbN)的电子结构;Rukmangad等[12]研究了高压下TbN和CeN的结构相变和弹性性质;Duan等[13]总结了稀土磷族化合物(REX,RE=La～Lu,X=N,P,As,Sb,Bi)的电子、磁学及其输运性质;Granville等[14]从实验和理论上研究了稀土氮化物的Raman光谱.本文采用基于密度泛函理论的平面波赝势方法,研究镧系氮化物的弹性性质、结构稳定性和光学及磁学性质等.

1 计算方法

采用基于密度泛函理论平面波基组的赝势从头算程序CASTEP进行计算[15].在优化结构和计算结构转变时,芯电子与价电子间的相互作用通过Vanderbilt[16]超软赝势(USP)描述,交换关联函数采用广义梯度近似(GGA)中的PBE(Perdew-Burke-Ernzerhof)处理[17].Brillouin区的k点积分通过Monkhorst-Pack方法实现,采用5×5×5网格.平面截断能选440 eV .本文采用BFGS(Borgden-Fletcher-Goldfarb-Shanno)算法对4个参数同时优化,其单原子收敛精度为(5.0×10-6)eV,原子的最大位移收敛精度为(5.0×10-5)nm,原子间相互作用力收敛精度为0.1 eV/nm,晶体内应力收敛精度为0.02 GPa.

在弹性常数计算过程中,芯电子与价电子间的相互作用和交换关联函数分别采用保模赝势和局域梯度近似(LDA)处理.为提高计算结果的准确性,计算时选用体积守恒应变模式.Brillouin区的k点积分通过Monkhorst-Pack方法实现,采用5×5×5网格.平面截断能选770 eV.

2 结果与讨论

2.1 弹性性质与结构稳定性 常压下镧系氮化物晶体的晶格常数、弹性常数和结构稳定性结果列于表1.其中体弹模量B表征材料抵抗断裂的能力,剪切模量G表征材料的抵抗塑性形变能力,Pugh[18]给出了判别晶体材料的塑性和弹性模量间的判别式B/G,即判别材料韧性与脆性的临界值为B/G=1.75.由表1可见: 在15个化合物晶体中,LaN晶体的弹性模量值最小,LuN晶体的弹性模量值最大,从LaN到LuN间弹性模量的变化未呈现明显的规律性,即f壳层电子个数对相应元素氮化物体弹模量大小的影响没有规律性;除LaN和GdN外,轻镧系元素(Ln=La,Ce,Pr,Nd,Pm,Sm,Eu)氮化物的B/G均大于1.75,表明这些晶体材料具有较好的韧性；重镧系金属元素(Ln=Gd,Tb,Dy,Ho,Er,Tm,Yb,Lu)氮化物的B/G均小于1.75,表明这些化合物晶体具有较明显的脆性.与文献[19]结果相符.

表1 常压下镧系氮化物晶体的晶格常数a、弹性常数Cij和结构稳定性Table 1 Cell parameters a,elastic constants Cij and structural stability of LnN at ambient pressure

2.2 光学性质 由于带间跃迁光吸收过程是电子在辐射电磁场微扰作用下从低能态跃迁至高能态的过程,因此体系在低频范围内对光电场的线性响应可由复介电常数ε(ω)=ε1(ω)+iε2(ω)描述,或用复折射率函数N=n+ik描述,其中实部为折射率,虚部为消光系数,满足关系:ε1=n2-k2,ε2=2nk.ε(ω)与光子和电子的相互作用密切相关,其虚部ε2(ω)可通过计算波函数的动量矩阵元得到,实部ε1(ω)可利用Kramer-Kronig关系[20]由ε2(ω)推出.其他光学常数可由ε1(ω)和ε2(ω)导出,如折射率n(ω)和反射系数R(ω)的表达式[21]为：

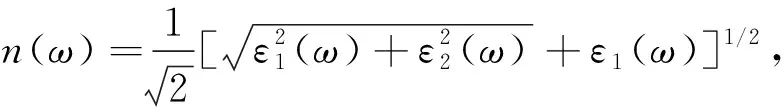
(1)

(2)

常压下镧系氮化物静态光学常数的计算结果列于表2,包括复介电常数实部ε1和虚部ε2、反射率R、复折射率实部n和虚部k.由表2可见,HoN的介电常数和反射系数最大,这是由于HoN的强磁性所致.

表2 常压下镧系氮化物晶体的静态光学常数Table 2 Static optical parameters of LnN at ambient pressure

2.3 Debye温度 由Debye温度可知晶格振动频率的数量级.其表达式[22]为

(3)

常压下镧系氮化物的横向声波速度vt、纵向传播速度vl、平均传播速度vm和Debye温度ΘD的计算结果列于表3.由表3可见,镧系氮化物晶体的Debye温度为300～500 K.计算结果表明,镧系氮化物声子振动频率的上限数量级为1013s-1.

表3 常压下镧系氮化物晶体的vt,vl,vm和ΘDTable 3 vt,vl,vmand ΘDof LnN at ambient pressure

综上所述,本文采用基于密度泛函的第一性原理方法,计算了镧系氮化物的弹性性质、光学性质和Debye温度.计算结果表明：轻镧系元素(Ln=La,Ce,Pr,Nd,Pm,Sm,Eu)氮化物(除LaN外)的体弹模量与剪切模量的比值B/G均大于1.75,即这些晶体材料表现为韧性；重镧系金属元素(Ln=Gd,Tb,Dy,Ho,Er,Tm,Yb,Lu)氮化物(除GdN外)的体弹模量与剪切模量的比值B/G均小于1.75,即这些晶体材料表现为脆性;HoN晶体具有较高的介电常数和光学反射率,这是由于HoN的强磁性所致;LaN晶体具有较高的折射率;镧系氮化物晶体中Debye温度最低的化合物是PmN,约为367 K,Debye温度最高的化合物是LuN,约为493 K.即镧系氮化物晶体声子振动频率的上限数量极为1013s-1.

[1] Vaitheeswaran G,Kanchana V,Rajagopalan M.Structural Phase Stability and Superconductivity of LaN [J].Solid State Commun,2002,124(3): 97-102.

[2] Ciftci Y O,Colakoglu K,Deligoz E,et al.The First-Principles Study on the LaN [J].Mater Chem Phys,2008,108(1): 120-123.

[3] Ghezail M,Amrani B,Cherchab Y,et al.Strucutral and Electronic Properties of LaN [J].Mater Chem Phys,2008,112(3): 774-778.

[4] Svane A,Szotek Z,Temmerman W M,et al.Electronic Structure of Cerium Monopnictides under Pressure [J].J Phys Condens Matter,1998,10(24): 5309-5325.

[5] Lee T Y,Gall D,Shin C S,et al.Growth and Physical Properties of Epitaxial CeN Layers on MgO (001) [J].J Appl Phys,2003,94(2): 921-927.

[6] Kanchana V,Vaitheeswaran G,Zhang X,et al.Lattice Dynamics and Elastic Properties of the 4fElectron System: CeN [J].Phys Rev B,2011,84(20): 205135.

[7] Olsen J S,Jφrgensen J E,Gerward L,et al.Compressibility and Structural Stability of CeN from Experiment and Theory [J].J Alloys Comp,2012,533(1): 29-32.

[8] Petukhov A G.Electronic Structure of Rare-Earth Pnictides [J].Phys Rev B,1996,53(8): 4324-4339.

[9] Larson P,Lambrecht W R L.Electronic Structure of Gd Pnictides Calculated within the LSDA+U Approach [J].Phys Rev B,2006,74(8): 085108.

[10] Leuenberger F,Parge A,Felsch W,et al.GdN Thin Films: Bulk and Local Electronic and Magnetic Properties [J].Phys Rev B,2005,72(1): 014427.

[11] Aerts C M,Strange P,Horne M,et al.Half-Metallic to Insulating Behavior of Rare-Earth Nitrides [J].Phys Rev B,2004,69(4): 045115.

[12] Rukmangad A,Aynyas M,Sanyal S P.Structural and Elastic Properties of Rare-Earth Nitrides at High Pressure [J].Indian J Pure Appl Phys,2009,47(2): 114-118.

[13] DUAN Chun-gang,Sabirianov R F,Mei W N,et al.Electronic,Magnetic and Transport Properties of Rare-Earth Monopnictides [J].J Phys Condens Mater,2007,19(31): 315220.

[14] Granville S,Meyer C,Preston A R H,et al.Vibrational Properties of Rare-Earth Nitrides: Raman Spectra and Theory [J].Phys Rev B,2009,79(5): 054301.

[15] Clark S J,Segall M D,Pickard C J,et al.First Principles Methods Using CASTEP [J].Zeitschrift für Kristallographie,2005,220(5/6): 567-570.

[16] Vanderbilt D.Soft Self-consistent Pseudopotentials in a Generalized Eigenvalue Formalism [J].Phys Rev B,1990,41(11): 7892-7895.

[17] Perdew J P,Burke K,Ernzerhof M.Generalized Gradient Approximation Made Simple [J].Phys Rev Lett,1997,78(7): 1396.

[18] Pugh S F.Relations between the Elastic Moduli and the Plastic Properties of Polycrystalline Pure Metals [J].Phil Mag,1954,45(367): 823-843.

[19] Iandelli A.Rare Earth Research [M].New York: McMillan,1961: 125.

[20] 方荣川.固体光谱学 [M].合肥: 中国科技大学出版社,2001: 39-51.

[21] ZHAO Rui,ZHANG Qi-zhou,ZHU Xiu-yun,et al.Structural Stabilities and Optical Properties of HgSe Calculated via First-Principles [J].Journal of Jilin University: Science Edition,2009,47(5): 1050-1053.(赵瑞,张启周,朱秀云,等.利用第一性原理计算HgSe的结构相变和光学性质 [J].吉林大学学报: 理学版,2009,47(5): 1050-1053.)

[22] SUN Zhi-mei,LI Sa,Ahuja R,et al.Calculated Elastic Properties of M2AlC (M=Ti,V,Cr,Nb and Ta) [J].Solid State Commun,2004,129(9): 589-592.