阻尼器对频率法拉索索力测量的影响*
2013-12-03淡丹辉陈艳阳
淡丹辉,陈艳阳
(同济大学桥梁工程系 上海,200092)
引 言
关键拉索索力对斜拉桥整体结构的受力和变形都有较大的影响,是桥梁健康监测和工作状态评估的重要依据,需要对其进行精确测量。基于环境振动的频率法是目前桥梁上常用的索力测量方法。采用频率法拉索索力测量的精度取决于高灵敏度拾振技术、精确的索结构频率测量与定阶以及频率与索力关系的准确度。多数桥梁的拉索减振是通过阻尼器来实现的。然而,阻尼器的安装改变了结构的动力特性,影响了频率法索力测量的精度。
目前,拉索索力的精确测量已有很多研究。苏成等[1]采用有限元方法及样条拟合技术拟合频率和索力之间的关系。任伟新等[2]采用能量法和曲线拟合方法,提出了分别考虑索垂度和抗弯刚度影响的、根据基频计算索力的使用公式。G.Ricciardi等[3]提出了考虑垂度和抗弯刚度的拉索连续振动分析模型。徐霞飞等[4]进行了拉索阻尼器的理论模型的求解。王修勇等[5]研究了斜拉桥拉索减振阻尼器对拉索索力测量的影响,其研究难以准确确定阻尼器安装高度及阻尼系数等对结构动力特性的影响程度,并未考虑阻尼器刚度因素。乔燕等[6]重点研究了垂度、阻尼器以及环境温度对振动频率法索力测试的影响程度。文献[7]提出了采用基于频率的系统识别方法进行索力评估。陈志庆[8]提出了考虑减振器影响的斜拉索索力测试研究,得到了索-阻尼器索力求解的公式,但公式的推导是假设索两端边界条件都为铰支,求解依赖于拉索形函数的假设,针对不同的拉索需要专门的分析,而且对于短索、垂度大的拉索以及多点支撑的拉索,该方法的适用性有待研究。
笔者依据自建的索-阻尼器有限元模型,从分析不同阻尼器参数对结构动力特性的影响出发,研究了阻尼器对采用频率法索-阻尼器体系索力测量的影响,提出了提高索-阻尼器体系索力测量精度的一些措施和建议。
1 频率法的索力测量
水平张紧索的自由振动方程为
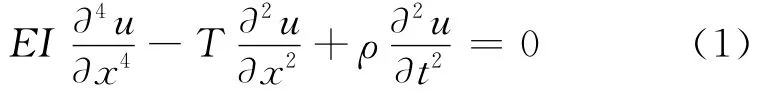
其中:x为沿索长方向的坐标;u(x,t)为t时刻索上各点的竖向位移;EI为索的抗弯刚度;T为拉索索力;ρ为拉索的线密度。
考虑拉索两端铰支时,由式(1)得到拉索平面内振动频率和索张力公式为

其中:n为索自振频率的阶数;fn为拉索的第n阶频率;L为拉索的计算索长。
拉索的频率受垂度、支撑方式及减震器等因素的影响,直接采用式(2)计算的索力会产生较大误差。为了确定阻尼器对式(2)索力计算精度的影响程度,根据式(2)分析了阻尼器引起的结构模态频率变化和索力测量误差的关系。假设阻尼器安装前、后拉索索力T保持不变,结构模态频率的测量和定阶是准确的,阻尼器引起的结构第n阶模态频率的相对变化记为Δfn/fn,则由频率变化引起、仍采用频率法计算索力的误差Terror为
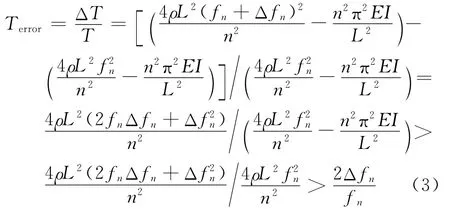
式(3)中高阶项(Δfn/fn)2很小,可以忽略。在忽略抗弯刚度的影响下,阻尼器对结构模态频率的影响在采用频率法索力计算时体现为索力测量误差为结构第n阶模态频率的相对变化的2倍。在本研究中,索模态频率误差Err(fn)定义为阻尼器阻尼系数造成的频率相对误差,其基准频率fnst为无外加阻尼装置且边界为铰支条件下(公式法理想适用条件)索的各阶模态频率。公式为
(2)活性材料投加量的确定。取3号废泥浆样品加入 AP2.0%、水泥20.0%、促凝增强剂CA 5.0%及相应添加剂,HHJ投加量不同,考察固化改良后浸出液主要指标,试验结果见表9。通过数据分析可以看出,当HHJ投加量达到10.0%时,固化改良物浸出液的各项指标都能够到要求。再增加投加量,处理效果变化不大,因此选择HHJ活性材料的加量为10.0%。
其中:n为频率阶数;fn为不同阻尼器阻尼系数下的第n阶频率。

2 拉索-阻尼器体系有限元模型
为了研究外加阻尼情况下频率公式法测量索力的准确性,必须要建立阻尼参数与拉索张力的解析关系,或者通过有限元模型计算二者关系。由于实际拉索的复杂性,垂度、边界条件和外置阻尼等因素,导致了利用解析法探讨二者关系变得很困难;因此,笔者通过有限元方法来讨论这一问题。
2.1 拉索-阻尼器体系有限元模型的建立
采用图1所示的拉索-阻尼器体系,应用MATLAB进行斜拉索的非线性有限元分析。假设拉索平衡时的线形为抛物线(在垂跨比小于1/8且忽略索的弯曲刚度时,可认为索的初始构形是抛物线形,程序中悬链线和抛物线计算出的体系前15阶频率的相对误差小于3‰),通过在重力作用下拉索的几何构型上划分有限单元来考虑垂度影响。采用平面梁单元模拟拉索结构,拉索边界条件取为刚接。拉索的单元质量矩阵采用一致质量矩阵模式。单元刚度矩阵包括弹性刚度矩阵、轴力刚度矩阵和弯矩刚度矩阵。不考虑拉索内阻尼,将阻尼器的阻尼定义为阻尼器单体实验时的标定阻尼系数,即阻尼力与速度的比值,考虑粘性阻尼器和摩擦型阻尼器两种类型,此外还考虑阻尼器刚度(轴向刚度)。
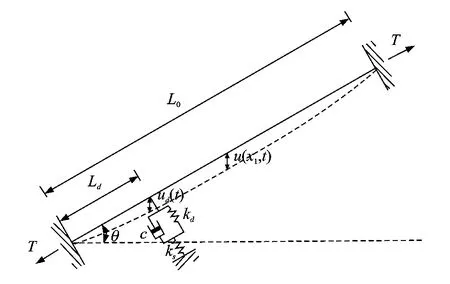
图1 拉索-阻尼器体系
2.2 模型正确性的验证
模型的正确性通过某斜拉桥B01号索的有限元分析来实现的。拉索参数如表1所示,其中:L为索长;T为初始索张力;E为拉索弹性模量;D为拉索直径;θ为拉索倾角;ρ为索线密度;Ld为阻尼器安装高度(从桥面算起,沿索长方向阻尼器安装位置)。
令Ld/L=0,C=0(Ns·m-1),即无阻尼情况,通过频率法计算拉索的基频为0.901 9Hz。有阻尼器情况下,程序计算的基频为0.947 7,相差5.1%,反映了本研究有限元程序的准确性。
3 阻尼器对索-阻尼器体系动力特性及索力测量的影响
阻尼器的有无会直接影响拉索的动力特性,也必然会对振动法测索力的精度产生影响。为了说明这一问题,以某斜拉桥B17号拉索为例,拉索参数如表2所示,阻尼系数取4×104Ns/m,利用有限元模型分析比较了阻尼器的有无对拉索索力测量误差的影响。

表1 某斜拉桥B01号索拉索参数
表2 某斜拉桥B17号拉索参数值
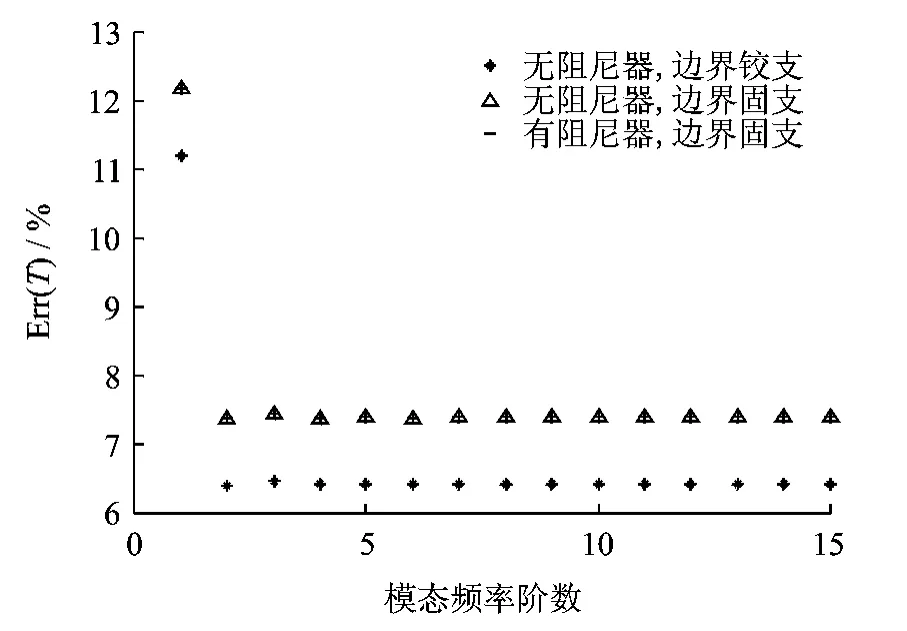
图2 有无阻尼器及不同边界条件下的索力误差
振动频率法只适用于边界条件为两端铰支且无阻尼器的情况。对于实际拉索,条件均在不同程度地偏离这个理想条件,结构的模态频率比铰支情况下略大。阻尼器通常引起拉索频率的增加,这些因素使得采用式(2)计算索力会产生较大误差。为了进一步研究这种影响程度和规律,下面分别考察阻尼器阻尼系数、阻尼器安装高度、阻尼器刚度等参数对拉索-阻尼器体系的模态频率及索力测量精度的影响。
3.1 阻尼系数
保持表3中拉索参数不变,改变阻尼系数,来考察阻尼大小对索-阻尼器体系动力特性和频率法索力测量的影响。
由图3(a)可知,在表3规定的条件下,在很大范围内,阻尼系数对索-阻尼器体系的前两阶频率几乎没有影响。当阻尼系数达到约6.45×104~6.46×104Ns/m之间时,如图3(b)所示,计算得到的一阶频率剧烈下降,在约64 585Ns/m时降低为零,此时对应的第2阶与远离临界阻尼(小于)时的第1阶频率近似相等。这种现象说明,模态频率存在临界阻尼系数,但达到一临界值时,该阶模态被完全抑制为零。
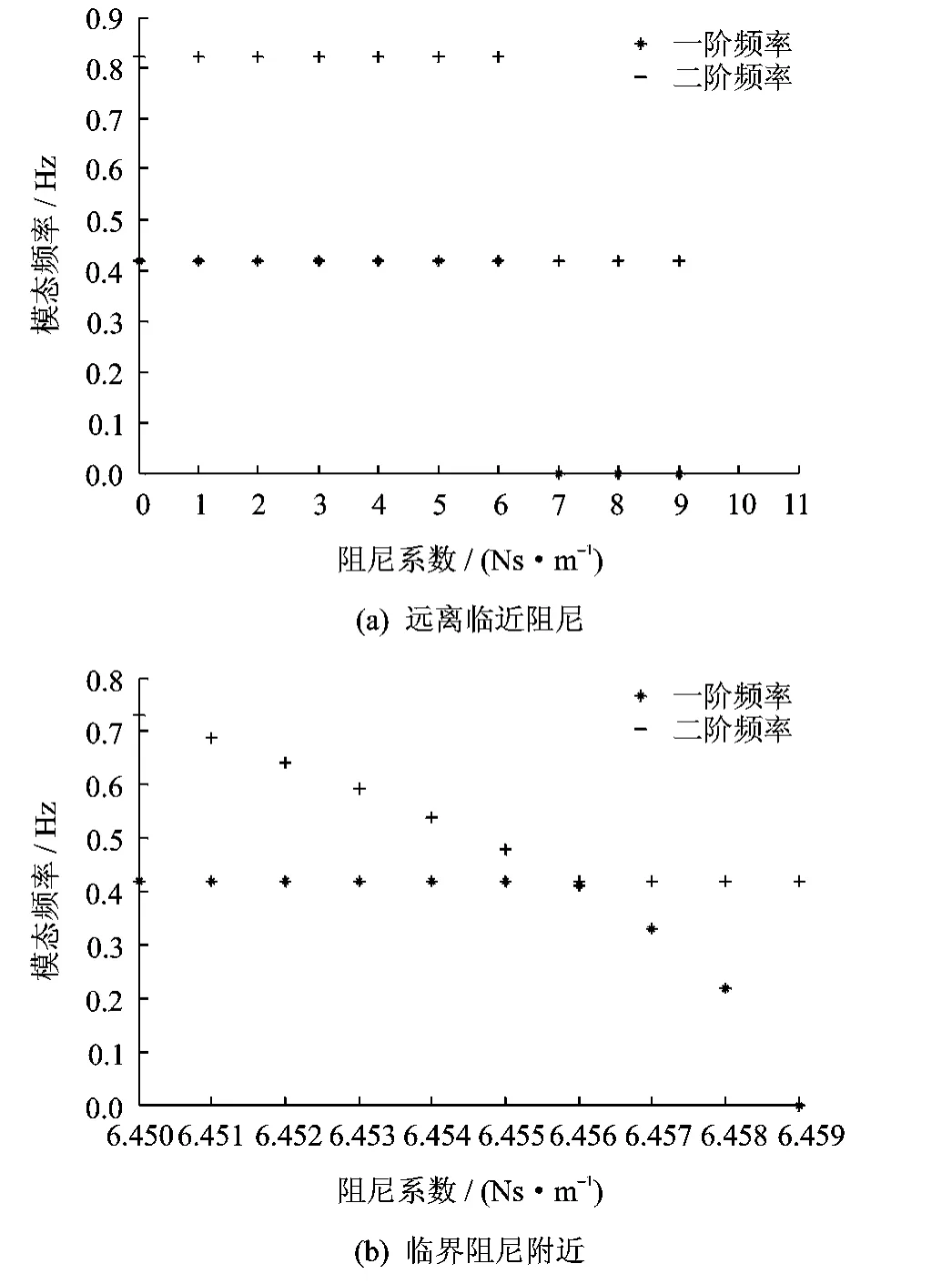
图3 阻尼系数对结构模态频率的影响
图4为阻尼系数对索模态频率误差和索力误差的影响情况。从图4(a)可以看出,采用前10阶模态频率进行频率公式法索力测量时,阻尼系数对频率相对误差有显著影响,阻尼系数越大,频率相对误差就越大。在阻尼系数小于1.2×105Ns/m时,模态频率阶数对这种影响起到加速作用。由图4(b)可见,阻尼系数对索力误差有着与阻尼系数对频率相对误差相同的趋势,这一趋势是式(3)的反映。可见,采用二阶频率的索力误差最小。
当阻尼系数达到系统的临界阻尼时,系统一阶频率为0,此时的二阶频率为系统的一阶频率(如图3所示),其他各阶均下移一阶。阻尼系数继续增大,新的结构一阶频率也会继续缓慢增加。当阻尼系数继续增大(约1×1010Ns/m时),新的各阶频率的增长速度随阻尼系数增大逐步降低为零。此时,索-阻尼器体系退化为在阻尼器安装位置处铰接的无阻尼体系。为此,表4给出了退化后索模型的前10阶频率。通过比较发现,当阻尼器达到1×1010Ns/m时,将阻尼器-拉索体系处理成铰支其误差较小,对低阶模态误差大,但不会超过0.4%。这说明在阻尼器大阻尼比的情况下,阻尼器的作用演变为一个普通的边界约束,体系朝长度变短的无阻尼索方向演变。在阻尼系数不接近无穷大、达到临界阻尼时,阻尼器位置处铰支的基频和二阶频率的误差仍有1.7%。可见,在阻尼系数达到临界阻尼而不接近无穷大时,将拉索-阻尼器体系当作在阻尼器安装位置处铰接的无阻尼体系会引起采用低阶频率索力测量的较大误差(约3.5%)。
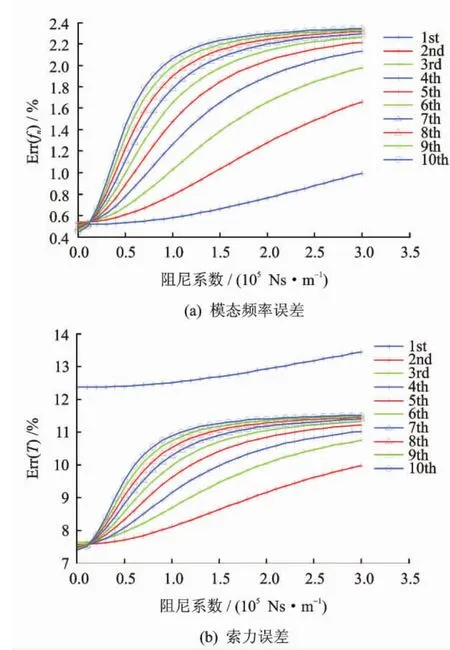
图4 阻尼系数对模态频率误差和索力误差的影响
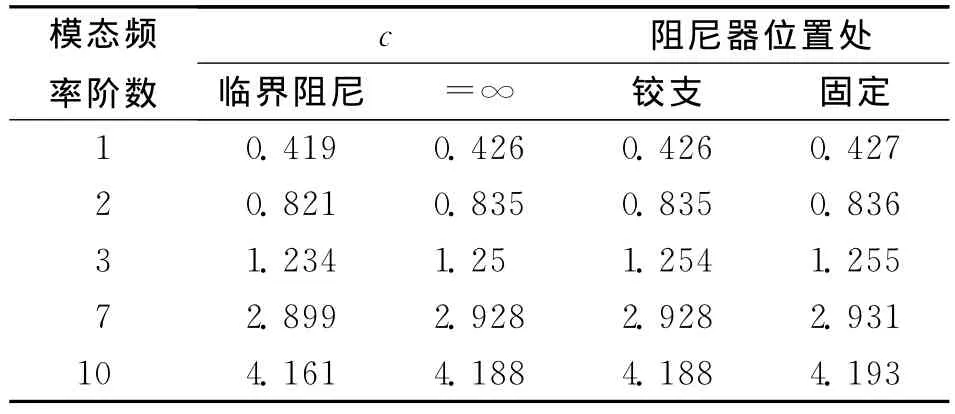
表3 阻尼系数对索-阻尼器体系的影响
3.2 阻尼器安装高度
拉索参数同表2,阻尼系数取4×104Ns/m,阻尼器安装高度[11]Ld/L从0.01变化到0.10。从图5(a)可见,对于前3阶模态,系统模态频率随阻尼器安装高度与其随阻尼器系数的变化趋势完全相同。阻尼器安装高度从3m增加到30m,前3阶频率误差的增幅分别达到1.8%,4.2%,7.6%。对于3阶以上模态,其频率误差和索力误差随阻尼器安装高度的变化无明显规律。阻尼器安装高度对体系的低阶模态频率影响较小,对高阶模态频率影响较大。从图5(b)可以看出索力误差随阻尼器安装高度的变化规律与频率误差相同。可见,阻尼器安装高度对结构的动力特性和索力测量影响显著。从索力误差结果来看,采用二阶频率计算索力具有相对较好的精度。
3.3 阻尼器刚度
拉索的减震阻尼器具有一定的刚度[9];因此,本研究讨论阻尼器刚度对索-阻尼器体系动力特性和频率法索力测量的影响。拉索参数同表3,通过改变阻尼器弹性模量来实现阻尼器刚度的改变,如图6所示。可以看出,频率误差和索力误差随着阻尼器刚度的增加有相同的变化趋势。阻尼器刚度越大,频率相对误差就越大,这种增大的趋势随着阻尼器刚度的增加而逐渐放缓。在阻尼器刚度达到8×106N/m时,这种增加几乎可以忽略。在阻尼器刚度小于2×106N/m时,各阶频率误差变化都很剧烈。当阻尼器刚度从0增加到4×106N/m时,阻尼器刚度对各阶频率影响都很大。例如,一阶频率误差变化达到1.4%时,对采用基频的索力影响可以达到3.6%。当阻尼刚度达到6×106N/m时,频率误差和索力误差都趋于一定值,说明此时增大阻尼器刚度对结构动力特性的影响已趋于稳定,结构的各阶模态频率只略微增大。阻尼器刚度对结构的低阶频率影响较大,对结构的高阶频率影响较小。文献[9]中阻尼器刚度的范围为1.2×106~1.4×106N/m。在这一范围内,阻尼器刚度对结构体系动力特性和频率法索力测量的影响比阻尼器安装高度小,但比阻尼系数影响大。索力误差表明,采用二阶频率计算索力具有相对较好的精度。
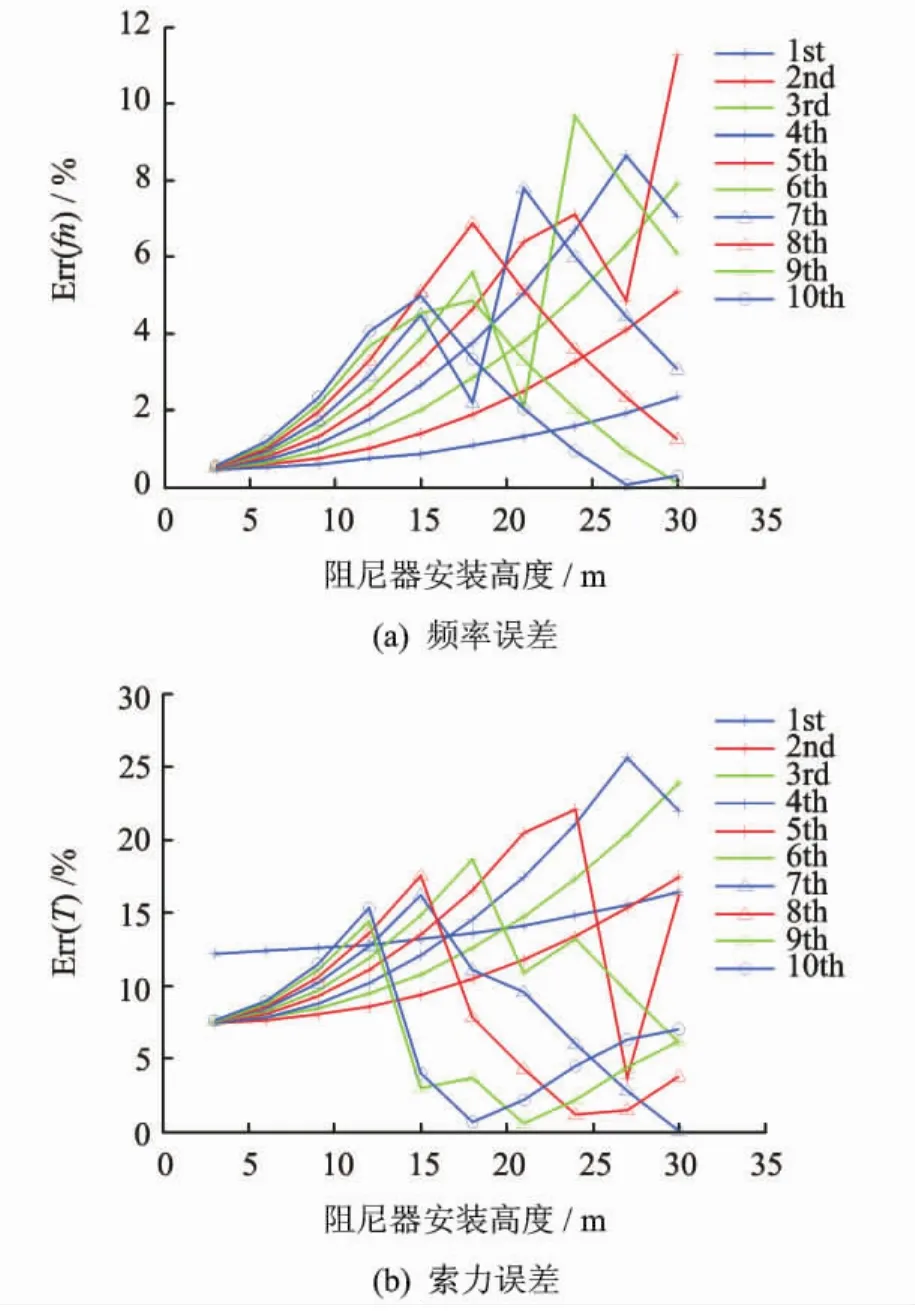
图5 安装高度对频率误差和索力误差的影响
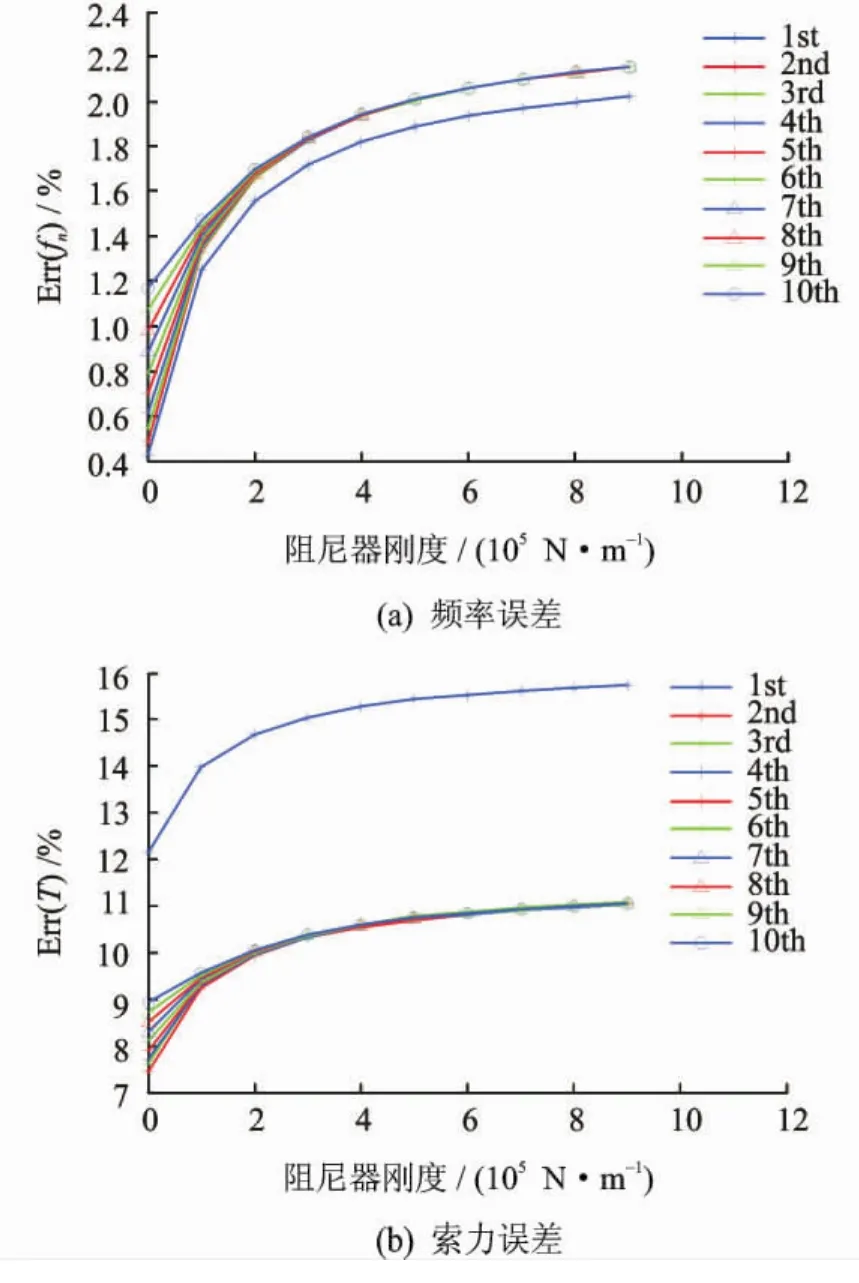
图6 阻尼器刚度对结构模态频率和索力测量的影响
以上研究是基于粘性阻尼器,对摩擦型阻尼器存在相同的结论。在阻尼器刚度小于2×106N/m时,带摩擦型阻尼器的拉索-阻尼器体系动力特性受外部激励影响较大。外部激励较小时,阻尼器刚度变化范围也很小,结构动力特性变化也较小;因此,在阻尼器刚度小于2×106N/m时,宜在外部激励较小时进行索力测量,在阻尼器刚度大于2×106N/m时,可采用与安装粘性阻尼器拉索相同的索力测量方法。
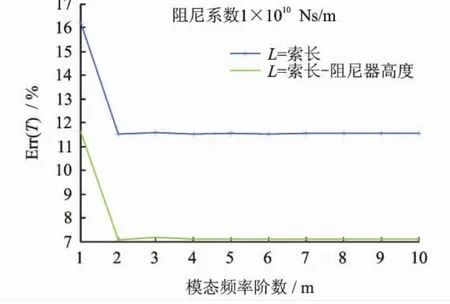
图7 修改索长方法的索力测量
4 提高索力测量精度的措施
拉索的高阶频率受阻尼器刚度的影响较低阶频率小,但其受阻尼系数及阻尼器安装高度影响较低阶频率大很多,而且变化无规律。由图4~6可知,采用拉索高阶频率计算索力是不合理的。由于阻尼器的嵌固作用,当阻尼器的阻尼系数超过系统的临界阻尼、刚度达到一定值时,拉索在阻尼器位置处近似铰支,相当于减小了拉索的有效振动长度。利用公式法计算的索力较真实索力有偏小的趋势,然而阻尼器的安装导致结构频率的增加,使得采用频率法测得的索力较真实索力有偏大的趋势。这两者影响程度相当,可以通过修改索长来抵消一部分,从而提高索力测量精度。拉索的有效索长取拉索索长L与阻尼器安装高度Ld的差。采用修改索长方法只能在一定程度提高索力测量的精度,计算索力与真实索力仍有一定的差距。由于阻尼系数对结构的低阶模态频率影响很小,对于阻尼系数未达到临界阻尼的情况,索力计算时应采用低阶频率。拉索参数同表3,采用修改索长公式较修改前提高了4.5%,但仍有7%的索力误差。
本研究发现,对于不同的阻尼器阻尼系数、安装高度和刚度采用拉索的2阶频率计算索力具有较好的精度。除了阻尼器刚度对结构的低阶频率影响较大外,阻尼系数及阻尼器安装高度对结构的前两阶频率影响都较小,尤其是对基频的影响最小;因此如果能够精确考虑拉索的垂度,采用基频计算拉索索力的公式来提高索力测量的精度(文献[2]、[4]等提到的公式只是分别考虑拉索垂度和抗弯刚度的)。直接采用索-阻尼器体系公式法求解也需要进一步研究。
5 结 论
1)阻尼器的阻尼系数、安装高度和刚度对结构的动力特性和索力测量影响都很显著。其中,阻尼系数和阻尼器安装高度对索-阻尼器的低阶频率影响较小,对高阶频率影响较大,阻尼器刚度对索-阻尼器的模态频率的影响与阻尼系数相反。在阻尼器刚度小于2×106N/m时,阻尼器刚度对结构体系动力特性和频率法索力测量影响比阻尼器安装高度小,但比阻尼系数影响大。
2)摩擦型阻尼器的索力测量在阻尼器刚度变化范围较小或阻尼器刚度较大的情况下,可以采用与粘性阻尼器相同的索力测量方法。
3)采用拉索的高阶频率来提高索力测量精度的措施是不合理的。修改索长方法适用于索-阻尼器体系的索力测量,能在一定程度提高索力测量精度。施加阻尼器会抑制拉索的低级振动,尤其是基频,而且拉索基频受垂度影响较大,按照式(2)进行索力计算时不宜采用基频,采用拉索的2阶频率可以获得较好的索力精度,式(3)在低阶频率范围内具有参考意义。
4)由于阻尼系数和阻尼器安装高度对索-阻尼器体系基频影响最小,在阻尼器刚度一定时,提出基于基频考虑垂度影响的索力测量方法可以提高索力测量精度。
[1] 苏成,徐郁峰,韩大建.有限元法及样条拟合技术在频率法测量索力中的应用[J].公路,2004(12):28-31.Su Cheng,Xu Yufeng,Han Dajian.Application of finite element method and spline fitting techniques on the measurement of cable force[J].Highway,2004(12):28-31.(in Chinese)
[2] 任伟新,陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005,38(11):26-31.Ren Weixin,Chen Gang.Practical formulas to determine cable tension by using cable fundamental frequency[J].China Civil Engineering Journal,2005,38(11):26-31.(in Chinese)
[3] Ricciardi G,Saitta F.A continuous vibration analysis model for cables with sag and bending stiffness[J].Engineering Structures,2008(30):1459-1472.
[4] 徐霞飞,任伟新.边界条件对吊索索力估算的影响[J].铁道科学与工程学报,2008,5(6):26-31.Xu Xiafei,Ren Weixin.Effect of boundary conditions on the estimation of suspender tension[J].Journal of Railway Science and Engineering,2008,5(6):26-31.(in Chinese)
[5] 王修勇,谭艳.斜拉桥拉索减振阻尼器对拉索索力测量的影响研究[J].振动与冲击,2008,27(11):80-82.Wang Xiuyong,Tan Yan.Study of cable tension measurement for stay cable attached with dampers[J].Journal of Vibration and Shock,2008,27(11):80-82.(in Chinese)
[6] 乔燕,孙传智.振动频率法测试斜拉桥拉索索力的应用研究[J].公路工程,2009,34(1):128-131.Qiao Yan,Sun Chuanzhi.Research on using of vibration frequency in measuring the cable tension for cablestayed bridge[J].Highway Engineering,2009,34(1):128-131.(in Chinese)
[7] Byeong H K,Taehyo P.Estimation of cable tension force using the frequency-based system identification method[J].Journal of Sound and Vibration,2007(304):660-676.
[8] 陈庆志.考虑减振器影响的斜拉索索力测试研究[D].长沙:湖南大学,2011.
[9] 梁栋,孙利民,陈纬,等.斜拉桥拉索减振油阻尼器的耐久性试验研究[J].同济大学学报:自然科学版,2007,35(10):1326-1330.Liang Dong,Sun Limin,Cheng Wei,et al.Durability test on oil damper for vibration control of stayed cable[J].Journal of Tongji University:Natural Science Edition,2007,35(10):1326-1330.(in Chinese)
[10]Krenk S.Vibrations of a taut cable with an external damper[J].Journal of Applied Mechanics,2000,67:772-776.
[11]邬喆华,楼文娟,陈勇,等.磁流变阻尼器对斜拉索半主动控制的最优参数[J].振动、测试与诊断,2006,26(1):41-45.Wu Zhehua,Lou Wenjuan,Chen Yong,et al.Optimail marker of MR damper for stay-cable with semi-active vibration control[J].Journal of Vibration,Measurement & Diagnosis,2006,26(1):41-45.(in Chinese)
E-mail:dandanhui@tongji.edu.cn
