数控加工中心高速电主轴运行状态测试*

王 民，张晋欣，昝 涛，南景洋，赵钦志，张 维

（1.北京工业大学机械工程与应用电子技术学院 北京，100124）

（2.国家机床质量监督检验中心 北京，100102）

引 言

数控加工中心正朝着高速、高精、高柔性、高可靠性的方向发展［1］。高速电主轴是彰显高档数控加工中心高速、高精的重要功能部件，其运行高平稳性和高可靠性是决定数控加工中心加工精度和加工效率的重要保证。由于国产高速电主轴在运行平稳性和可靠性方面与国外同类产品具有较大差距，因此有必要对国产高速电主轴进行试验测试分析，确定影响其性能提高的部件故障和设计缺陷等原因。电主轴在运行过程中的平稳性差主要体现在其振动和噪音异常上，笔者以某机床厂生产的卧式加工中心高速电主轴作为研究对象，通过试验模态测试和试验阶次测试相结合的方法识别导致其在高速运行过程中振动加剧的原因。试验与分析结果表明，与常用的振动频谱分析方法相比，阶次分析和试验模态测试相结合进行综合分析诊断能够更加准确地确定高速电主轴中由旋转部件缺陷和电主轴结构设计、制造与装配导致的振动和噪声异常的多种原因。

1 试验基本原理

笔者采用阶次分析试验［2－5］与试验模态测试［6－7］相结合的方法对加工中心高速电主轴进行了综合性能测试与分析。与传统振动监测分析方法相比，阶次分析方法采用等角度增量采样［8］代替等时间间隔采样，可有效地对高速电主轴升、降速实验中的非平稳信号进行分析，获取高速电主轴运行过程中存在的与其传动部件相关的设计、制造及装配缺陷。

电主轴传动部件的缺陷会导致电主轴运行的平稳性变差，使电主轴运行过程中出现额外过大的附加动态载荷。当动态载荷与电主轴或机床结构固有模态频率相接近的时候会加剧电主轴及数控机床在其模态频率处的振动，影响加工精度及加工效率，进一步加剧了电主轴部件缺陷的恶化速度及出现故障的概率。为此采用试验模态分析方法获取电主轴及机床结构可能被激发的各阶模态固有频率及振型等参数，通过分析试验模态结果确定机床结构抗振薄弱环节以及可能导致电主轴部件出现故障的主轴和机床结构上的设计缺陷。

2 试验仪器及过程

2.1 试验仪器

试验采用丹麦BK公司的测试仪器，包括6通道前端、MM0024红外线测速计、4507单向加速度传感器和力锤等。

2.2 试验过程

2.2.1 阶次测试

为了获得较好的振动信号，在电主轴的x，y两方向分别放置一个4507单向加速度传感器。MM0024红外线测速计放置在距离电主轴大约30cm处。以电主轴转速为参考转速，每隔1s转速增加100，直到8kr／min后停止。测试分布如图1所示。

图1 振动阶次测试测点及转速计分布

2.2.2 模态测试

采用单点激励多点响应的方法对电主轴进行模态测试。在电主轴前轴承外部与电主轴三坐标各方向成45°处用力锤激励，其激励点及响应点分布如图2所示。

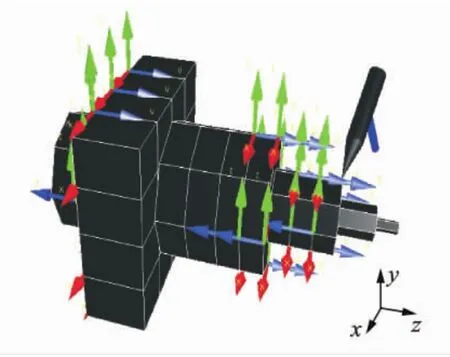
图2 模态测试激励点与响应点分布

3 试验结果分析

3.1 阶次测试结果

试验结果表明，电主轴在x方向和y方向的振动阶次谱图中阶次成分相类似。电主轴x方向振动信号的阶次谱图如图3所示。从图3可以看到，两条虚线箭头所示为100Hz与128Hz固有频率曲线，圆圈所示固有频率为1 111Hz，方框所示固有频率为4 110Hz，多条竖直线说明测试点振动信号中存在以主轴转速为基频的多个阶次上存在剧烈的强迫振动现象，这些直线代表阶次如图顶部数字所示。

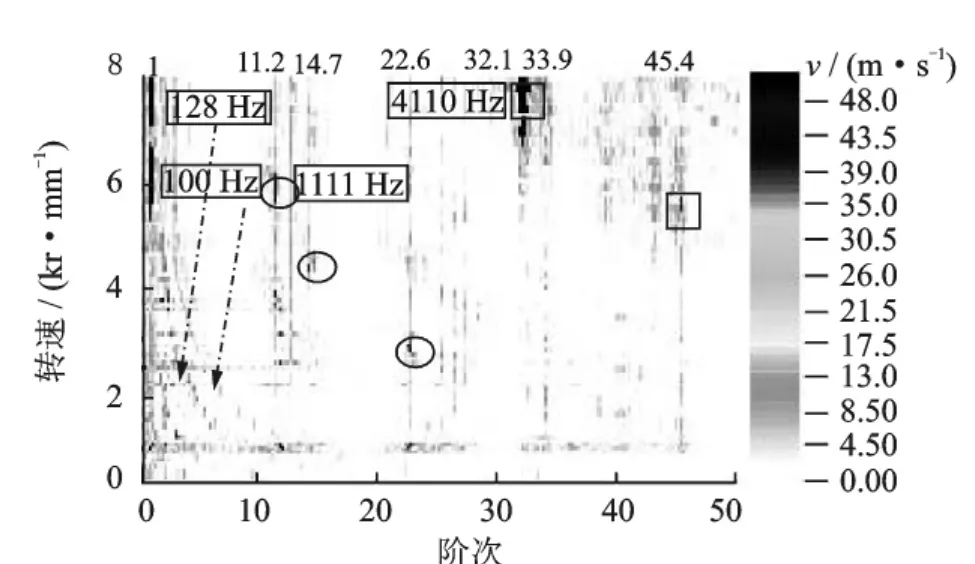
图3 电主轴x方向振动阶次谱图

电主轴x方向振动剧烈的阶次 分别为：1，11.2，14.7，22.6，32.1，33.9，45.4。其中，1阶次处的强迫振动表明与主轴基频相关。动平衡［9］存在缺陷导致的振动频率随主轴转频变化的强迫振动，尤其当主轴转频逐渐接近机床结构某阶固有频率时会发生共振现象，导致振动剧烈，如图1中1阶线上100Hz和128Hz两处。

如图3所示，电主轴的振动阶次谱图中存在约为主轴1阶基频转速的11.2倍频现象，如图1中顶部所标1阶、11.2阶、22.6阶、33.9阶和45.4阶。通过计算轴承故障特征频率［10］发现当主轴前轴承外环出现波纹和点蚀等缺陷时，会出现类似于图3阶次图中的倍频现象。理论计算的轴承故障特征频率，即外环的波纹点蚀故障特征频率Fa分别为11.27fi，22.55fi，33.82fi，45.10fi。其中，fi为主轴转频。

倍频数据根据公式［11］计算得出

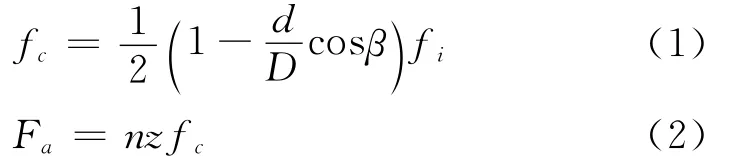
其中：fc为外环的某一点与一个滚动体接触的频率；d为滚珠直径；D为轴承节径；β为接触角；z为滚珠数，n为自然数。

测试的主轴前轴承相关结构参数为：β＝18°，d＝9mm，D＝89mm，z＝25。

同时，11.27阶次也是主轴前轴承内、外环变形导致振动异常的故障特征频率，计算公式为

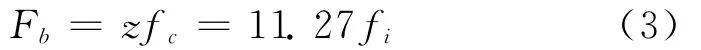
通过计算电主轴后轴承故障特征频率发现，滚动体波纹引起的3阶振动频率与由阶次分析得到的转频32.1阶次相近。滚动体波纹故障特征频率Fc分别为：11.03fi，21.61fi，32.20fi。

数据依据下列公式得出

其中：fb为滚动体的某一点与内环或者外环接触的频率。

主轴后轴承结构参数分别为：β＝17.88°，d＝6.84mm，D＝72.96mm，z＝24。

根据电主轴前、后轴承故障特征频率计算结果，可以看出导致振动阶次异常的原因是电主轴动平衡问题以及前、后轴承的一些缺陷引起的。例如，前轴承外环存在精加工面波纹、缺陷（点蚀）以及内外环变形；电主轴后轴承滚动体存在波纹。综合考虑机器情况，振动剧烈的主要原因是由于电主轴固有频率被激发或主轴在制造装配过程中存在误差导致内、外环变形，进而振动加剧。

3.2 模态测试结果

通过阶次分析测试可以看出，随着转速的变化，电主轴在某些固有频率处发生振动明显剧烈的共振现象。为了找出电主轴及机床结构中引起共振的薄弱环节，对电主轴和加工中心主体结构进行试验模态测试。测试结果发现，与阶次测试中振动明显的1 111Hz和4 110Hz相近的固有频率为1 101Hz和4 110Hz。从它们的振型中可以清楚看到电主轴前、后轴承振动明显，其振型如图4，5所示。图中虚线为电主轴无振动时的位置，实线为振动时的位置。可以看出，电主轴前、后轴承在固有频率为1 101Hz，4 110Hz时振动明显。

图4 1 101Hz前轴承处沿x方向摆动

图5 4 110Hz后轴承处沿x方向摆动

通过激励主轴前端还获取了加工中心主体结构中立柱结构的各阶模态振型和模态频率。用于驱动主轴箱垂直方向运动的丝杠副安装在立柱结构中的左侧立柱上，该侧立柱承担了主轴和主轴箱的大部分重量和动态载荷。通过模态振型发现，模态频率分别为100Hz和130Hz的两阶模态振型为装有丝杠的左侧立柱的一阶和二阶弯曲变形，其振型如图6，7所示。

图6 100Hz立柱弯曲变形

图7 130Hz立柱弯曲变形

结合阶次分析结果可以得出结论，主轴运行不平稳激发起了电主轴前、后轴承处变形和装有丝杠的一侧立柱的两阶弯曲变形的4个模态振动，是机床的结构设计薄弱环节。由于存在薄弱环节，机床结构抗振性能差也导致了主轴轴承内、外圈变形等异常现象，恶化了机床的抗振能力；因此有必要对电主轴和立柱的设计薄弱环节重新进行结构优化设计以提高其抗振性。

4 结 论

1）导致电主轴高速运行状态下振动加剧与主轴转频相关的强迫振动主要是由于电主轴动平衡差、运行过程中内、外环变形较大及后轴承滚动体表面存在波纹等因素。

2）机床主轴和主体结构的机械结构设计存在薄弱环节。例如，电主轴前、后轴承处和装有丝杠的一侧立柱抗振性差，导致机床运行过程中振动剧烈，加剧了主轴轴承缺陷影响及故障发生的机率；因此需要对薄弱环节重新进行结构优化设计以提高其抗振性。

［1］ 熊建武，周进，张克昌，等.浅论高速加工中心的发展和特点［J］.科技信息，2007（15）：336－337.Xiong Jianwu，Zhou Jin，Zhang Kechang，et al.On the characteristics and development of the high speed machining center［J］.Science Information，2007（15）：336－337.（in Chinese）

［2］ 孟杰，陈小安，陈锋.高速电主轴的试验模态分析［J］.机械设计，2009，26（6）：452－454.Meng Jie，Chen Xiaoan，Chen Feng.Experimental modality analysis of high speed motorized spindle［J］.Journal of Machine Design，2009，26（6）：452－454.（in Chinese）

［3］ Bai Mingsan，Huang Jiamin，Hong Minghong，et al.Fault diagnosis of rotating machinery using an intelligent order tracking system［J］.Journal of Sound and Vibration，2005，280：699－718.

［4］ Pan M C，Lin Y F.Further exploration of Vold－Kalman filtering order tracking with shaft－speed information I：theoretical part，numerical implementation and parameter investigation［J］.Mechanical Systems and Signal Processing，2006，20：1134－1154.

［5］ Pan M C，Wu C X.Adaptive Vold－Kalman filtering order tracking［J］.Mechanical Systems and Signal Processing，2007，21：2957－2969.

［6］ Kim S M，Ha J H，Jeong S H，et al.Effect of joint conditions on the dynamic behavior of a grinding wheel spindle［J］.International Journal of Machine Tools and Manufacture，2001，41（12）：1749－1761.

［7］ 张飞.大型龙门铣床关键件的动态测试与分析［D］.北京：北京工业大学，2009.

［8］ 汪伟，杨通强，王红.非稳态信号计算阶次分析中的重采样率研究［J］.振动、测试与诊断，2009，29（3）：350－351.Wang Wei，Yang Tongqiang，Wang Hong.Research on resampling of order tracking analysis of non－stationary signals［J］.Journal of Vibration，Measurement ＆Diagnosis，2009，29（3）：350－351.（in Chinese）

［9］ 黎飞龙，吴宝勤，李光辉.某小型涡扇发动机转子高速动平衡试验［J］.兵工自动化，2010，29（6）：81－84.Li Feilong，Wu Baoqin，Li Guanghui.Experiment on high speed dynamic balance of certain type small turbofan engine rotor［J］.Ordnance Industry Automation，2010，29（6）：81－84.（in Chinese）

［10］周井玲，陈建春，陈晓阳，等.三点接触轴承球疲劳试验机特征频率计算［J］.轴承，2010（10）：28－30.Zhou Jingling，Chen Jianchun，Chen Xiaoyang.Characteristic frequency calculation of fatigue life tester for ballswith three points contact［J］.Bearing，2010（10）：28－30.（in Chinese）

［11］徐冠基，柏林，刘小峰，等.基于阶比分析的风力发电机噪声音调判定［J］.振动、测试与诊断，2010，30（4）：452－454.Xu Guanji，Bo Lin，Liu Xiaofeng，et al.Determination of the tonality of wind turbines acoustic noise aased on order analysis［J］.Journal of Vibration，Measurement＆ Diagnosis，2010，30（4）：452－454.（in Chinese）