多楔带动态特性及带 轮间摩擦系数的测试分析－*

上官文斌，曾祥坤，刘泰凯，段小成，王亚杰

（1.华南理工大学机械与汽车工程学院 广州，510641） （2.宁波拓普集团股份有限公司 宁波，315806）

引 言

多楔带集平型带的高柔韧性和V型带的高功率性为一体，具有使带－轮驱动系统结构紧凑、传递功率大、带的寿命长及系统振动和噪声小等优点，被广泛应用于汽车发动机前端附件驱动（front end accessory drive，简称FEAD）系统［1－3］。FEAD系统主要通过带－轮间的摩擦力传递动力，振动特性主要包括：两轮间带段的纵向振动（表现为沿着带速度方向的张力波动）、横向振动（表现为垂直带速度方向的横向振动位移）、带－轮间的滑移和各轮的旋转角度波动。带的纵向刚度和阻尼系数、弯曲刚度以及带－轮间的摩擦系数是影响FEAD系统振动特性的重要参数，也是FEAD系统振动特性计算分析的主要参数［4］。

多楔带的纵向刚度和阻尼系数特性受带长的影响较大。在工程实际中通常采用带的纵向弹性模量和阻尼系数－刚度比系数来表征带的纵向力学性能参数［5］。国外的研究学者对多楔带的纵向力学性能参数、弯曲刚度和带－轮间摩擦系数进行了实验研究［6－9］。多楔带的结构型式是典型的弹性体结构，其动刚度与激励振幅、激励频率和带的初始张力有关。Cepona等［7］采用锤击激励的方法，测试了带长对带的纵向弹性模量和阻尼系数的影响。该方法无法测试和研究激振振幅、激励频率对带的纵向动刚度和阻尼系数的影响，测试结果无法全面表征带的纵向力学性能。另外，在测量带横向振动固有频率的实验中采用电磁激振器激励多楔带（质量为49g），并在被测带段上粘贴了20g的小质量块用于激振器顶杆前端力传感器与皮带的固连。这就增加了带的附加质量，引起带段横向振动固有频率的实测值与理论值之间产生较大误差，从而影响带段弯曲刚度的计算结果。国内对FEAD系统动态特性的研究起步较晚，用于计算分析FEAD系统动态特性时，其带的参数和带－轮间的摩擦系数主要参考国外文献中的数据［10－13］。

笔者以汽车用6PK型多楔带为测试对象，测量了带的纵向静态和动态特性、弯曲刚度和带－轮间的摩擦系数。测试分析了带长、初始张力、激振振幅和激励频率对带的纵向动刚度和阻尼系数特性的影响。建立了表征带的纵向动刚度和阻尼系数特性与带长、初始张力、激振振幅和激励频率关系的多项式模型和指数函数模型。由于带的质量较小，用力锤敲击可以激起带在横向方向的共振，得到带横向振动的共振频率。采用最小二乘方法拟合理论计算的固有频率（与带的弯曲刚度有关）和实测的固有频率，得到带的弯曲刚度。此方法避免了文献［7］在带上增加附加质量用来连接激振器而影响实测带在横向方向的共振频率，从而影响带弯曲刚度计算结果的实验方法。笔者还建立了带－轮间摩擦系数测量的实验装置、数据处理方法和测试流程，并测试带的初始张力、带－轮间的包角、轮的转速对带－轮间摩擦系数的影响。

1 实验装置和测试原理

图1为PK型多楔带的横截面结构示意图［14］。由图1可见，汽车用PK型多楔带由顶布、张力线、缓冲胶和楔胶等组成，带的楔角为40°。楔胶的作用是使带与轮之间产生摩擦力。缓冲胶的作用是传递摩擦力和承受垂直于带速度方向的压力。张力线用于承受带沿其速度方向的张力。顶布主要用来保护张力线。

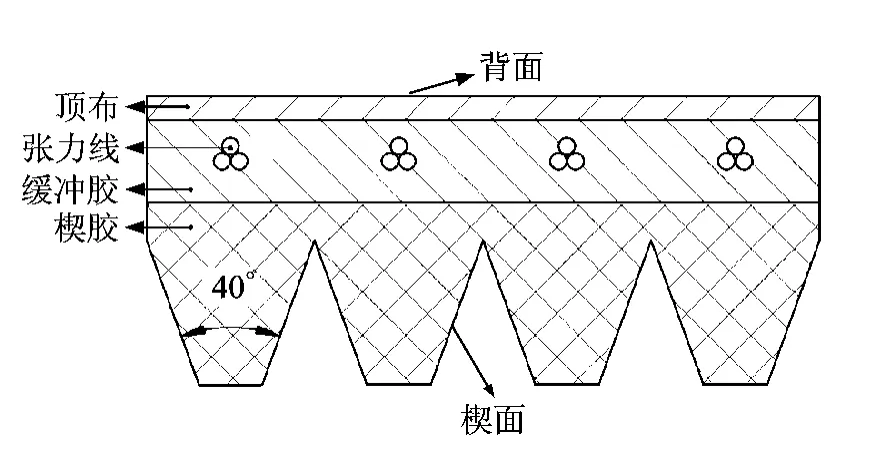
图1 汽车用PK型多楔带横截面结构示意图

以汽车用6PK型多楔带为研究对象，分别介绍带的纵向静刚度、纵向动刚度和阻尼系数、弯曲刚度、带－轮间摩擦系数的实验装置和测试原理。

1.1 纵向静刚度实验

多楔带的纵向静刚度实验主要是测量带的纵向力－位移曲线。该实验在 MTS 831弹性体测试仪（以下简称MTS测试仪）上完成，实验装置如图2所示。由图2可见，多楔带一端固定在MTS测试仪上的作动端，另一端安装在固定端。带的张力信号由安装在作动端上的力传感器测得。测试前，在MTS测试仪的控制系统中设置带的张力范围和作动端的运动速度。在多楔带被拉伸两个力循环后，MTS测试仪的数据处理系统采集作动端的位移信号和力信号，得到带的纵向力－位移曲线。

图2 多楔带纵向静刚度、动刚度和阻尼系数特性实验装置

1.2 纵向动刚度和阻尼系数实验

1.2.1 采用MTS测试仪测量带的纵向动刚度和阻尼系数

采用MTS测试仪测量带的纵向动刚度和阻尼系数特性的实验装置如图2所示。实验前，在MTS测试仪的控制系统中设置带的初始张力、作动端的位移激振振幅和激励频率范围。实验时，由MTS测试仪的数据处理系统记录作动端的位移信号与力信号，并基于传递函数方法计算带的纵向动刚度和滞后角［15］。

滞后角反应了位移滞后于力的角度，表征被测元件阻尼的大小，工程上常用阻尼系数来表示。阻尼系数的计算式［15］为

其中：C为带的阻尼系数；K 为带的纵向动刚度；φ为滞后角；ω为激励圆频率。

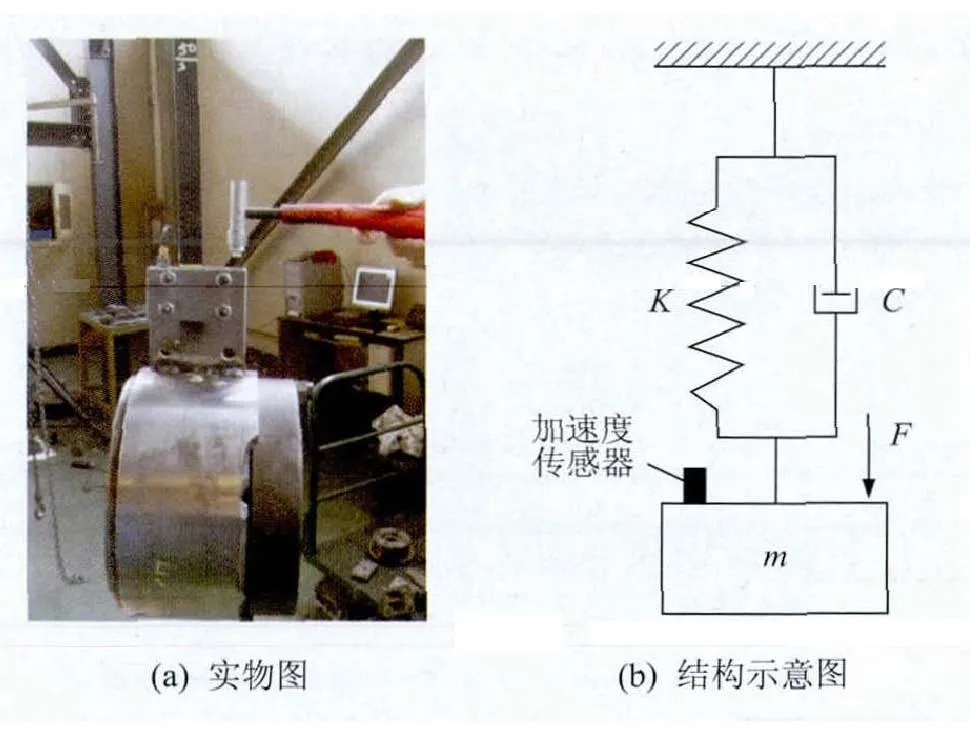
图3 锤击法测量带纵向动刚度和阻尼系数特性的实验装置

1.2.2 采用锤击法测量带纵向动刚度和阻尼系数

采用锤击法测量多楔带纵向动刚度和阻尼系数的实验装置如图3所示。由图3（a）可见，带的上端固定在横梁上，下端固定于焊接在质量块上的夹紧板上。加速度传感器用于测量质量块沿带纵向的加速度信号。由带与质量块组成的有阻尼单自由度弹簧质量系统的结构示意图如图3（b）所示。

实验时，沿带的纵向用激励锤对夹紧板施加随机冲击激励。用Bruel ＆Kjaer Pulse System采集激励力信号和质量块的加速度信号，并分析得到质量块的加速度－力幅频响应曲线。带的纵向动刚度和阻尼系数的计算式［7］为

其中：m为质量块的质量；ω0为带的纵向固有频率；Δω＝ω2－ω1为半功率带宽；ω1，ω2为半功率点对应的激励频率。

将带看成没有弯曲刚度的轴向运动弦线，带的纵向动刚度理论计算式为

其中：E为带的纵向弹性模量；A为带的横截面积；L为带的长度。

由式（2），（3）得到带的纵向弹性模量E和阻尼系数－刚度比系数λ的计算式［5］分别为

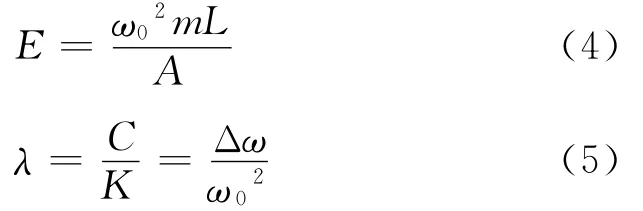
1.3 弯曲刚度实验

多楔带弯曲刚度实验在MTS测试仪上完成，实验装置如图4所示。激光位移传感器用于测量带段中点的横向（垂直带速度的方向）位移。实验前，由MTS测试仪的控制系统设置带的初始张力，用游标卡尺测量带的长度。

由于带的质量较小，用力锤敲击可以激起带在横向方向的共振，得到带横向的共振频率。此方法避免了文献［7］在带上增加附加质量用以连接激振器而影响实测带在横向方向的共振频率，从而影响带弯曲刚度计算结果的实验方法。

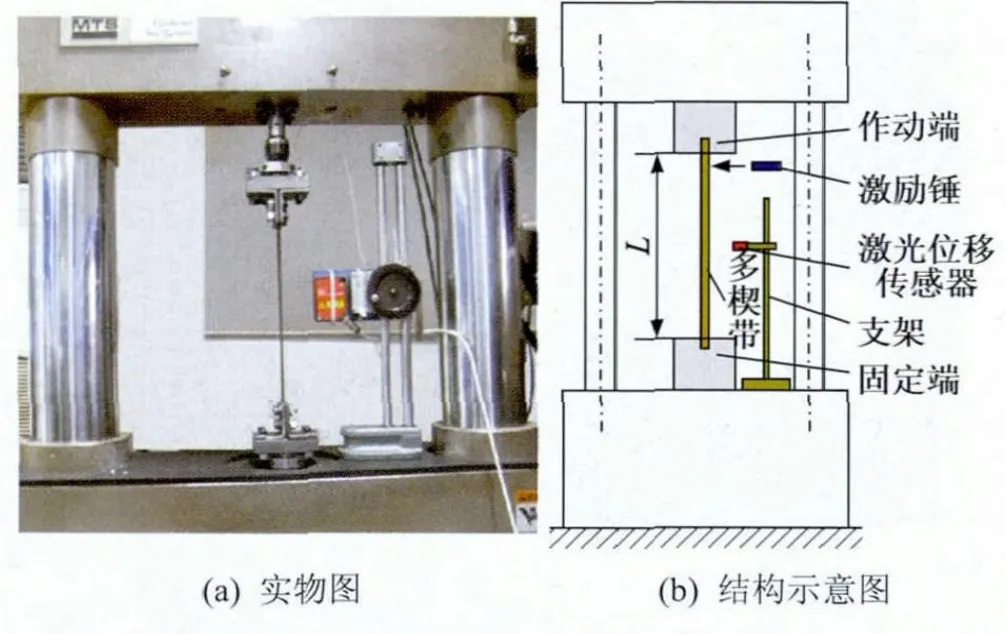
图4 多楔带弯曲刚度的实验装置

实验时，在靠近被测带的上端用激励锤沿带的横向施加随机冲击激励，如图4（b）所示。用Bruel＆Kjaer Pulse System采集激励力信号、带段中点的横向振动位移信号。根据带横向振动位移－力幅频响应曲线可识别出带横向振动的固有频率。

考虑带的弯曲刚度，图4中两端固定的带段可看成是两端固定的简支梁。带横向振动的第i阶固有频率f0i为弯曲刚度EI的函数，理论计算式［7］为

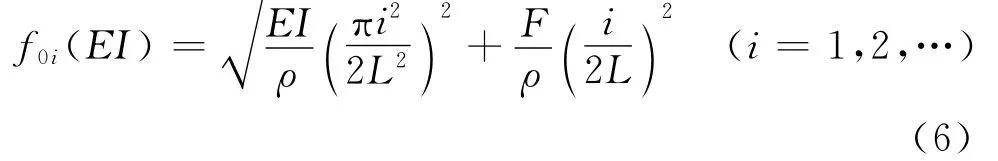
其中：ρ为带的线密度（0.096kg／m）；F 为带的初始张力。

由最小二乘方法确定带的弯曲刚度EI

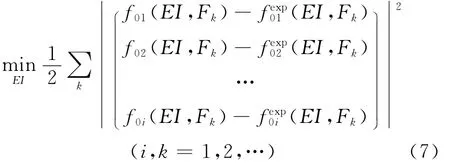
其中：Fk为第k次调节作动端位移后带的初始张力；f0i为带横向振动的第i阶固有频率计算值；fexp0i为带横向振动的第i阶固有频率实测值。

式（7）取最小值时的EI为带的弯曲刚度。

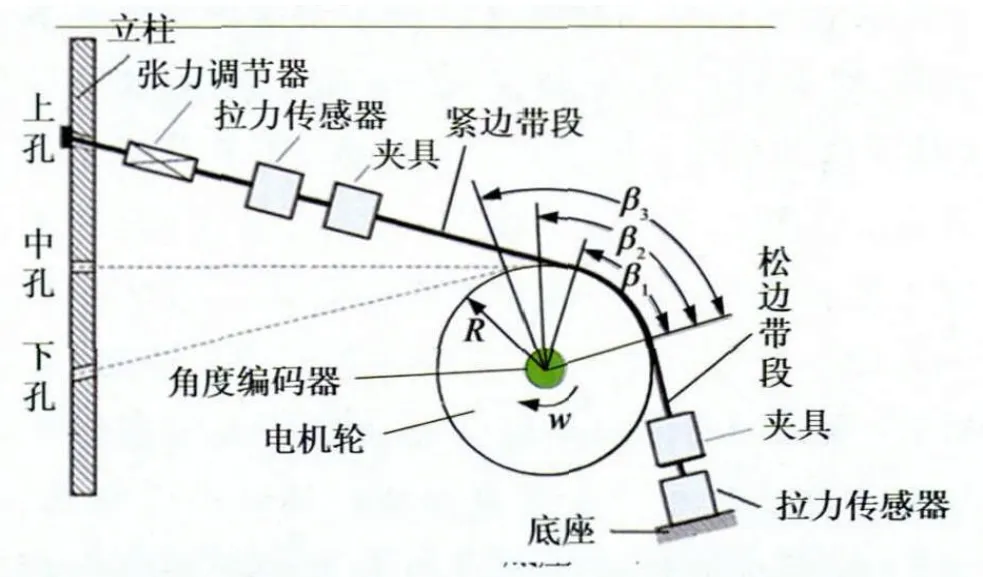
图5 带－轮间摩擦系数的实验装置结构示意图

1.4 带－轮间摩擦系数实验

带－轮间摩擦系数实验主要是测量带的楔面与楔带轮、带的背面与平带轮间的摩擦系数（以下简称带的楔面和背面与轮间的摩擦系数）。设计了带－轮间摩擦系数测量的实验装置，结构示意图如图5所示。可见：当电机轮顺时针方向旋转时，靠近立柱侧的带段为紧边带段，靠近底座侧的带段为松边带段；带与轮间以一定的包角相互接触；张力调节器分别与立柱的上孔、中孔、下孔相连接来调节带与轮间的包角；电机的转速由变频器来调节。实验时，Bruel＆Kjaer Pulse System通过角度编码器采集电机轮的转速信号，通过拉力传感器采集紧边和松边带段的张力信号。假设带在轮上打滑，且带－轮间的力传递完全由带－轮间接触面的摩擦力提供（忽略其他摩擦的影响）。由Euler－Eytelwein方程得到轮两侧紧边和松边带段的张力关系［9］为

其中：Td为紧边带段的张力；Tj为松边带段的张力；β为带－轮间的包角；μ为带－轮间摩擦系数。

由式（8）得到带－轮间的摩擦系数μ的计算式为

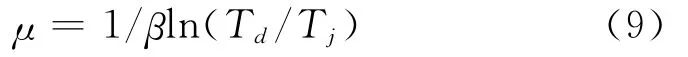
2 实测结果与分析

2.1 纵向静刚度

在MTS测试仪的控制系统中，设置拉伸张力范围为100～2 000N，作动端的运动速度为5mm／min。带的初始长度为370mm时，实验测得带的纵向力－位移曲线如图6所示。可见，带在拉伸和卸载中，力－位移曲线为一迟滞回线，表征了带的结构阻尼特征。加载曲线与卸载曲线近似线性变化。根据加载曲线和卸载曲线斜率的平均值计算出带的纵向静刚度为704N／mm。

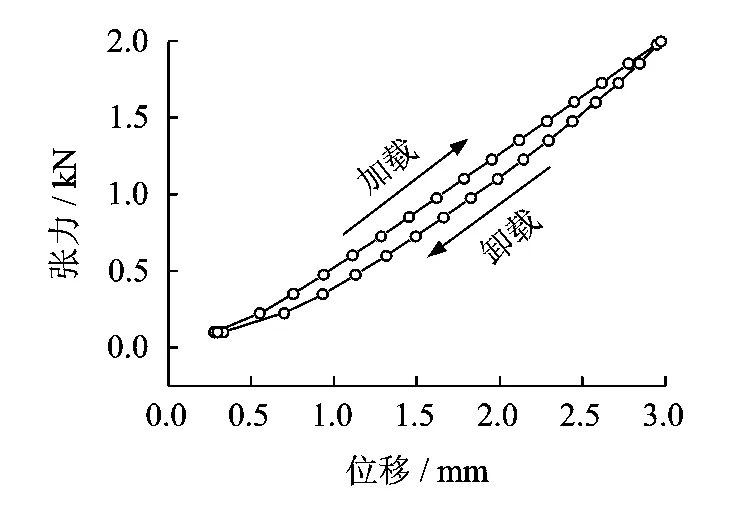
图6 带的纵向静态力－位移曲线（L＝370mm）

2.2 纵向动刚度和阻尼系数

2.2.1 利用MTS测试仪实测的结果与分析

在MTS测试仪的控制系统中分别设置带的初始张力（F＝300N和450N）、作动端的位移激振振幅（Am＝0.1mm，0.3mm 和0.5mm）和激励频率范围为2～200Hz（频率间隔为2Hz）。以3根不同长度（L＝270mm，370mm，450mm）的6PK型多楔带为测试对象，分别测试和分析带的长度、激振振幅和初始张力对带纵向动刚度、滞后角和阻尼系数的影响。

1）带的长度不同

带的张力（450N）与激振振幅（0.3mm）一定时，实验测得不同带段长度下带的纵向动态特性如图7所示。可见，带的长度、初始张力和激振振幅一定、激励频率增加时，带的纵向动刚度略有增大，但阻尼系数减小。由图7（a）可见，带长增加，带的纵向动刚度减小。带长和激励频率对滞后角的影响较小，如图7（b）所示。带长对阻尼系数的影响也较小，如图7（c）所示。当激励频率与带的固有频率相同或接近时，会引起带的共振，在图7（a）中表现为动刚度值突然减小。实验发现，带在纵向拉力作用下发生共振时，带的横向振动位移较大。这说明激励频率与带的横向振动固有频率相接近引起了带的共振。由图7（a）可见，带长增加，带的同阶次横向振动固有频率降低。

2）激振振幅不同

带的初始张力（300N）与带长（370mm）一定时，在不同激振振幅下实验测得带的纵向动态特性如图8所示。可见：当带的初始张力、带长一定时，带的纵向动刚度随激励频率的增加略有增加，而阻尼系数随激励频率的增加而减小；激振振幅增加时，带的纵向动刚度减小，带的滞后角和阻尼系数变化不大。

3）带的初始张力不同

当激振振幅（0.3mm）与带长（370mm）一定、带的初始张力不同时，实验测得带的纵向动态特性如图9所示。可见，带的初始张力增加，带的纵向动刚度、带的同阶次横向振动固有频率均增大；带的滞后角略有减小；阻尼系数变化不大。

由图8（a）和9（a）可见，带长为370mm 时，不同工况下带的纵向动刚度在715～1 090N／mm范围内。根据带纵向动刚度值与静刚度值的比值可计算出带纵向刚度的动静比范围为1.02～1.55。

采用锤击法实验测得3根不同长度带的纵向动刚度和阻尼系数，由式（4），（5）计算出带的纵向弹性模量和阻尼系数－刚度比系数如表1所示。

由表1可见，质量块质量相同时，带长越短，带的阻尼系数、纵向动刚度越大，而带的纵向弹性模量越小；带长一定，质量块质量减小，带的纵向动刚度和阻尼系数略有减小。这说明带长对带的纵向动刚度和阻尼系数影响较大，而带的张力对带的纵向动刚度和阻尼系数影响较小。通常取表1中各组实验

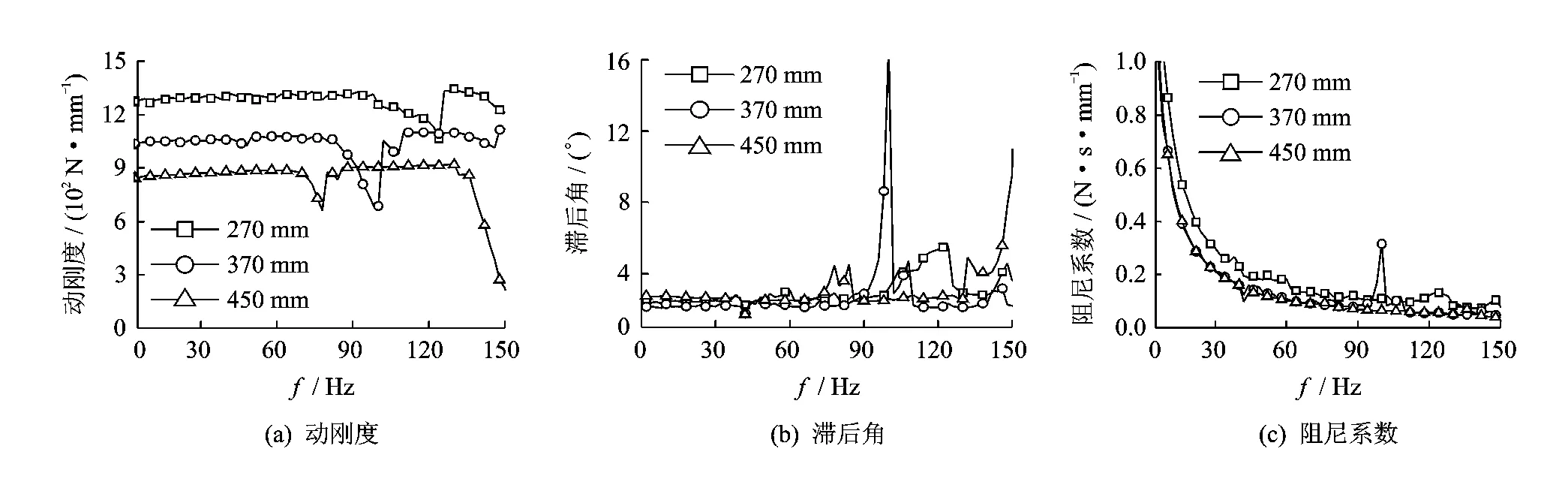
图7 带长对带的纵向动刚度、滞后角和阻尼系数特性的影响（F＝450N，Am＝0.3mm）

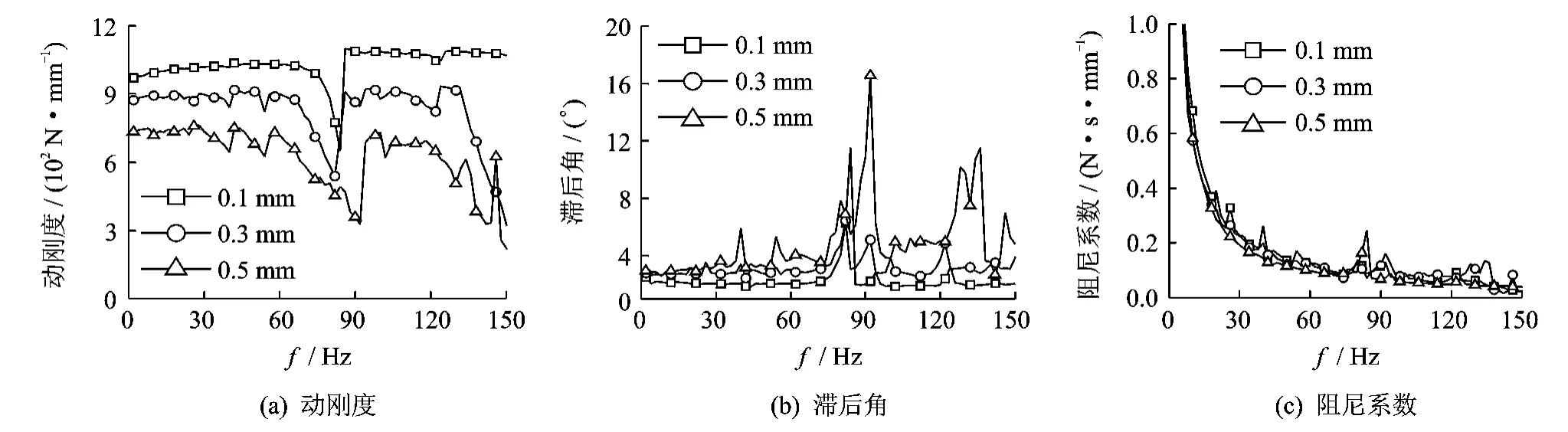
图8 激振振幅对带的纵向动刚度和阻尼系数特性的影响（F＝300N，L＝370mm）

图9 初始张力对带的纵向动刚度和阻尼系数特性的影响（Am＝0.3mm，L＝370mm）

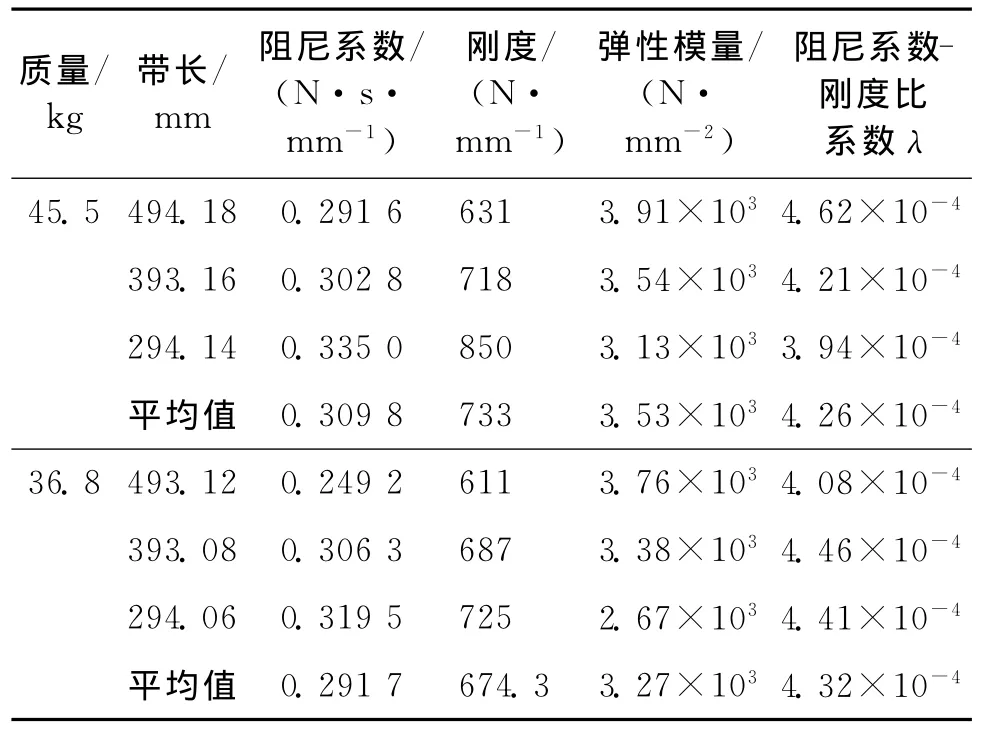
表1 锤击法实验测得带的纵向弹性模量和阻尼系数－刚度比系数

带的弹性模量的平均值、阻尼系数－刚度比系数的平均值来表征带纵向力学性能参数［7］

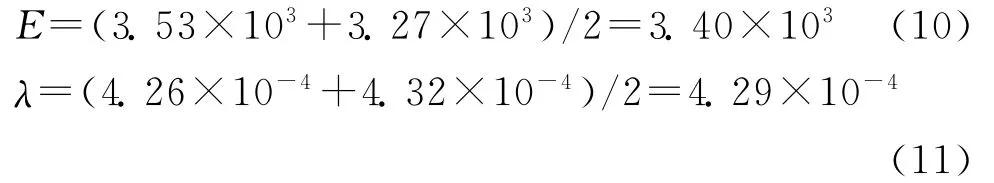
将式（10），（11）代入式（3），（5）中，计算不同带长下带的纵向动刚度和阻尼系数。

2.2.3 两种实验装置测试结果对比

由表1可见，带长为294.14mm、质量块质量为45.5kg时，由锤击法实验测得带的纵向动刚度为850N／mm、阻尼系数为0.335N·s／mm。选择与锤击法实验相同的带段（带长为290mm、带的初始张力为450N），由MTS测试仪测得不同激振振幅下带的纵向动刚度和阻尼系数特性如图10所示。

由图10可见，激振振幅在0.1～0.5mm区间内，由MTS测试仪测得带的纵向动刚度在950～1 350N／mm范围内；带的阻尼系数范围为0.1～1.0N·s／mm。

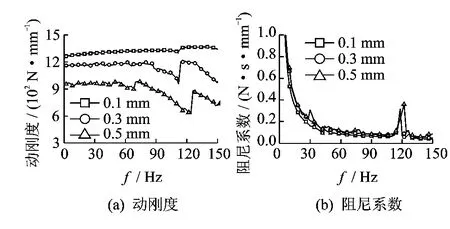
图10 不同激振振幅下带的纵向动刚度和阻尼系数特性（F＝450N，L＝290mm）

对比以上两种实验方法的测试结果表明，带长和带的初始张力一定时，锤击法实验测得的带的纵向动刚度和阻尼系数为常数；而MTS测试仪测得的带的纵向动刚度和阻尼系数受激励频率和激振振幅的影响较大。由于多楔带主要是由橡胶材料组成，带的纵向动态特性不仅与带的长度有关，而且还与激振振幅、激励频率和带的初始张力有关；因此，采用MTS测试仪的实验结果能更好地表征带的纵向动态特性。

式中：下标1和2分别表示整流侧和逆变侧换流站，在不影响损耗计算精度的条件下，考虑系统传输有功与整流侧吸收有功相等。

以下分别建立多项式模型和指数函数模型用于计算带的纵向动刚度和阻尼系数，并基于MTS测试仪的实验数据采用最小二乘方法识别模型参数。

1）带的纵向动刚度

由图7（a），8（a）和9（a）可见：带的纵向动刚度受带的长度、激振振幅和初始张力影响较大；带的纵向动刚度随激励频率的增加近似线性增大。这里采用多项式拟合带的纵向动刚度

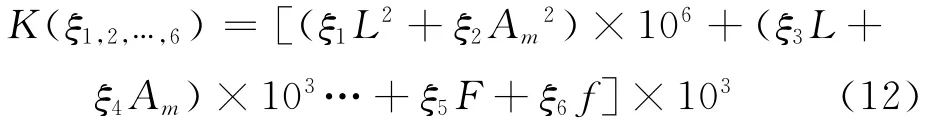
其中：ξi（i＝1，2，…，6）为带的纵向动刚度模型拟合系数；f为带的激励频率。

采用最小二乘方法求解式（12）中的拟合参数

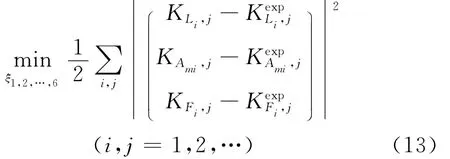
根据式（13）计算出带纵向动刚度模型中的拟合系数ξi（i＝1，2，…，6）＝－0.011 9，－76.677 7，5.741 6，－48.254 9，1.437 7，0.795 9。根 据 式（12）计算得到带的纵向动刚度值与实验值对比，如图11所示。可见，采用式（12）可较好地拟合不同工况下带的纵向动刚度。

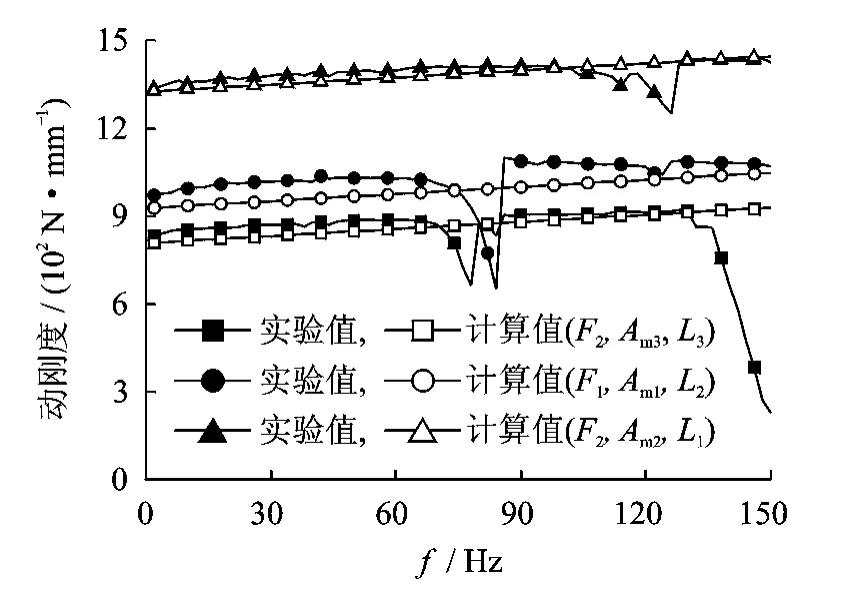
F1＝300N，F2＝450N；Am1＝0.1mm，Am2＝0.2mm，Am3＝0.3mm；L1＝270mm，L2＝370mm，L3＝450mm图11 带的纵向动刚度计算值与实验值对比

2）带的阻尼系数

由图7（c），8（c）和9（c）可见，带的激励频率比带的长度、激振振幅和初始张力对阻尼系数的影响要大得多；因此，只考虑激励频率（f）对带阻尼系数的影响，采用指数函数拟合带的阻尼系数

其中：ζi（i＝1，2，…，5）为带的阻尼系数模型拟合系数。

采用最小二乘方法求解式（14）中的拟合系数

由式（15）计算出带阻尼系数模型中的拟合系数ζi（i＝1，2，…，5）＝6.178 7，2.017 7，0.927 7，17.349 8，54.629 2。根据式（14）得到带的阻尼系数计算值与实验值对比如图12所示。

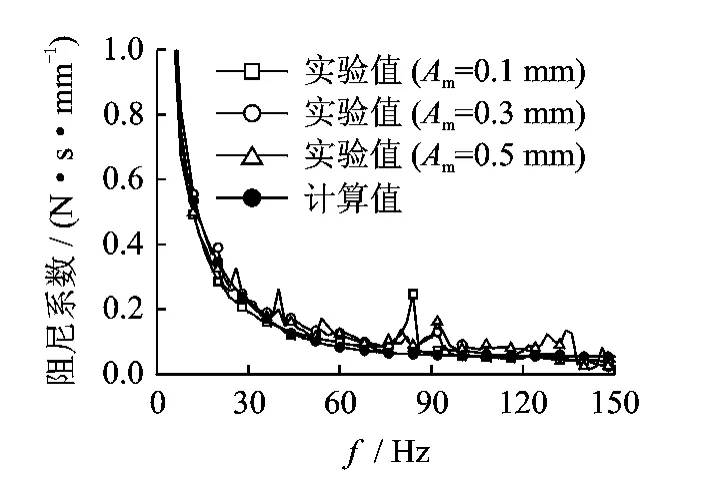
图12 带的阻尼系数计算值与实验值对比（F＝300N，L＝370mm）

可见，不同工况下带的阻尼系数计算值与实验值吻合较好。这说明式（14）能较好地表征带的阻尼系数与激励频率的关系。

2.3 弯曲刚度

带的初始长度一定（438mm）、张力不同时，实验测得该带段中点的位移－力幅频响应曲线如图13所示。根据图13可以较容易地识别出带横向振动的前3阶固有频率。这说明采用锤击方法可以较容易使带在横向方向产生共振。

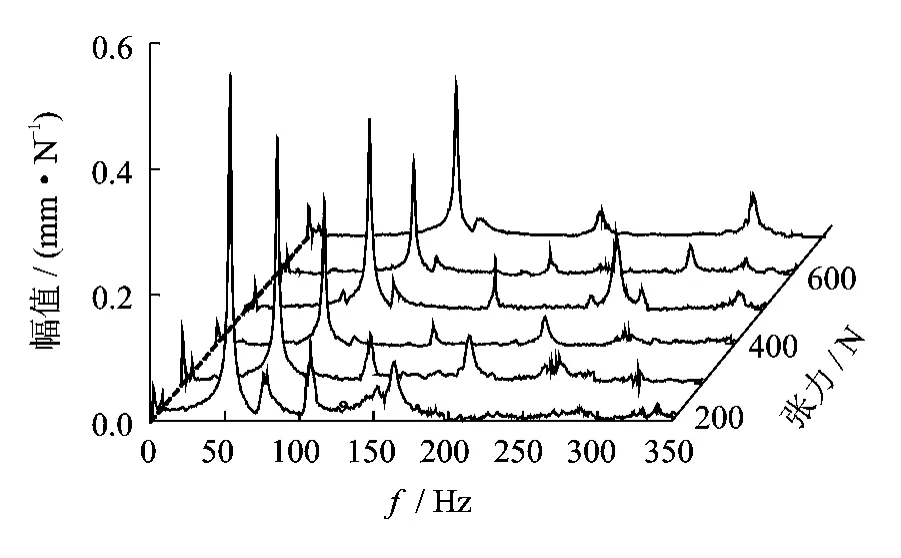
图13 带横向振动位移－力幅频响应曲线（L＝438mm）

同理，实验测得其他两根多楔带（带长分别为370mm和270mm）中点的横向振动位移－力幅频响应曲线，并从幅频响应曲线中识别出带横向振动的前3阶固有频率值。由式（7）计算出各带段的弯曲刚度如表2所示。可见：带长越短，带的弯曲刚度越大；当带的张力、长度一定时，带的第i（i＝1，2，…）阶固有频率值近似等于第1阶固有频率的i倍；带长相同时，带横向振动的各阶固有频率随带的张力增加而增大。

表2中带的弯曲刚度随带长的增加近似线性减小。采用线性拟合的方法，将带的弯曲刚度表示成带长的函数关系

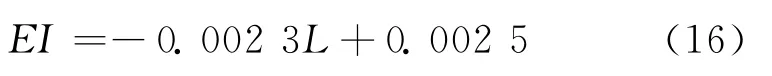
其中：L为带段的长度。

表2 多楔带的前3阶横向振动固有频率实测值及其弯曲刚度

2.4 带－轮间的摩擦系数

带的楔面与轮接触，带的初始张力（400N）和带－轮间包角（66.13°）一定、轮的转速从零匀加速到110r／min时，实验测得紧边和松边带的张力、轮的转速随时间变化关系曲线如图14（a）所示。可见，电机运转前，紧边和松边带段的初始张力均为400 N，电机转速从0～110r／min，紧边带段张力逐渐增大，松边带段张力逐渐减小；电机在110r／min左右稳定旋转时，紧边带段和松边带段的张力也各自趋向稳定（Td＝610N，Tj＝86N）。由式（9）计算得出带－轮间的摩擦系数随时间变化的关系曲线如图14（b）所示，取摩擦系数稳定值1.69为该工况下带的楔面与轮间摩擦系数。

采用相同的测试方法和数据处理方法，分别测试和分析带的初始张力（F＝200N，400N和600N）、带－轮 间 包 角 （β＝ 53.15°，66.13°和78.79°）、轮的转速（n＝50r／min，100r／min和150 r／min）对带的楔面（背面）与轮间摩擦系数的影响。根据多组实测数据得到带的楔面（背面）与轮间摩擦系数的取值范围。

2.4.1 带初始张力

当 轮 的 转 速 （100r／min）和 带－轮 间 包 角（66.13°）一定、带的初始张力不同时，带－轮间的摩擦系数如图15所示。可见，当带的初始张力由

图14 带的楔面与轮间摩擦系数的测试结果（F＝400N，n＝100r／min，β＝66.13°）

200N增加到600N时，带－轮间摩擦系数略有增大。这是因为带的初始张力过小，带与轮间的接触面没有充分接触，此时带－轮间的摩擦力相对较小。但是，当带的初始张力继续增加，带－轮间的摩擦系数将趋于某一稳定值。

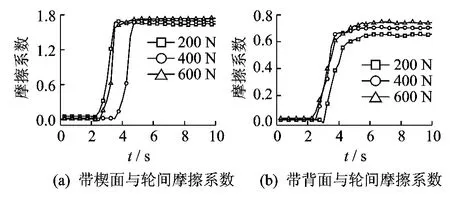
图15 带的初始张力对带－轮间摩擦系数的影响（β＝66.13°，n＝100r／min）

2.4.2 带－轮间包角

当带的初始张力（200N）和轮的转速（100r／min）一定、带－轮间包角不同时，带－轮间的摩擦系数如图16所示。可见，带的初始张力和轮的转速一定时，带－轮间包角增加，带楔面（背面）与轮间摩擦系数也略有增加，但变化很小。

2.4.3 轮转速

当带的初始张力（200N）和带－轮间包角（53.15°）一定时，轮的转速对带－轮间摩擦系数的影响如图17所示。可见，轮的转速对带与轮间摩擦系数影响很小。2.4.4 摩擦系数变化范围

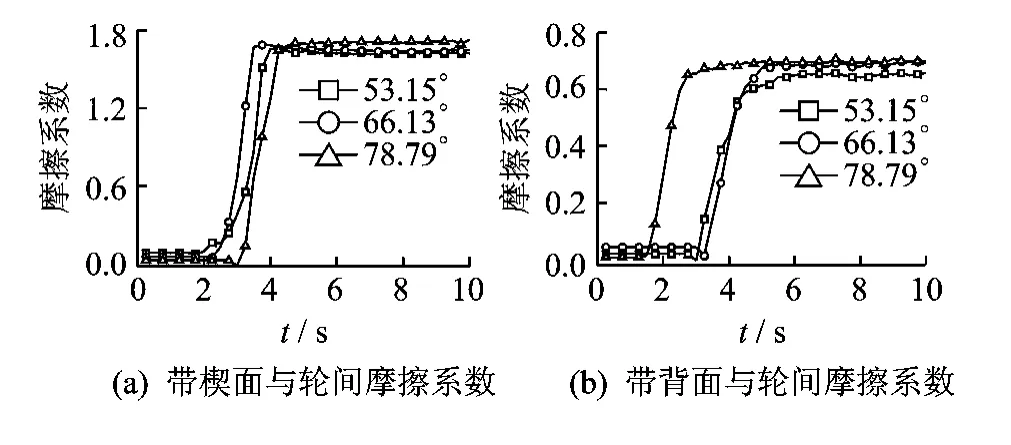
图16 带－轮间包角对带－轮间摩擦系数的影响（F＝200N，n＝100r／min）

图17 轮的转速对带－轮间摩擦系数的影响（F＝200N，β＝53.15°）

当带的初始张力、带－轮间包角、轮的转速（n1＝50r／min，n2＝100r／min）不同时，带的楔面（背面）与轮间摩擦系数μ1（μ2）实测结果如表3所示。由表3可见，带的楔面和背面与轮间摩擦系数的取值范围分别为1.63～1.80和0.64～0.78。

表3 带的楔面（背面）与轮间摩擦系数实测结果

3 结 论

1）带的纵向静态力－位移特性曲线为一迟滞回线，且加载、卸载曲线均近似线性变化。

2）带长越短、激振振幅越小、带的初始张力越大，带的纵向动刚度越大；带的阻尼系数随激励频率的增加而减小。与锤击法实验结果相比，MTS 831弹性体测试仪的测试结果能更好地表征带的纵向动刚度和阻尼系数特性。

3）采用多项式模型、指数函数模型分别拟合带的纵向动刚度和阻尼系数特性。结果表明，带的纵向动刚度和阻尼系数计算值与实验值吻合较好，验证了带的纵向动刚度和阻尼系数模型是正确的。

4）带长越短，带的弯曲刚度、同阶次横向振动固有频率越大；带的弯曲刚度随带长的增加而线性减小。

5）带的初始张力和带－轮间包角增加，带－轮间的摩擦系数略有增大；轮的转速对带－轮间摩擦系数影响较小。

［1］ Hwang S J，Perkins N C，Ulsoy A G，et al.Rotational response and slip prediction of serpentine belt drives systems［J］.ASME Journal of Vibration and Acoustics，1994，116（1）：71－78.

［2］ Leamy M J，Perkins N C.Nonlinear periodic response of engine accessory drives with dry friction tensioners［J］.ASME Journal of Vibration and Acoustics，1998，120（4）：909－916.

［3］ Parker R G.Mechanics of serpentine belt drives with belt bending stiffness［J］.Journal of Applied Mechanics，2005，127（5）：957－966.

［4］ Sandhu J S，Wehrly M K，Perkins N C，et al.Design kit for accessory drives（DKAD）：dynamic analysis of serpentine belt drives［C］∥SAE 2003Noise and Vibration Conference and Exhibition.Grand Traverse，Michigan：SAE International，2003：1－10.

［5］ Kraver T C，Fan G W，Shah J J.Complex modal analysis of a flat belt pulley system with belt damping and coulomb－damped tensioner［J］.Journal of Mechanical Design，1996，118（2）：306－311.

［6］ Michon G，Manin L，Remond D，et al.Parametric instability of an axially moving belt subjected to multifrequency excitations：experiments and analytical validation［J］.Journal of Applied Mechanics，2008，75（4）：1－8.

［7］ Cepona G，Maninb L，Boltezar M.Introduction of damping into the flexible multibody belt－drive model：a numerical and experimental investigation［J］.Journal of Sound and Vibration，2009，324（1－2）：283－296.

［8］ Meckstroth R J.Accessory drive belt／pulley friction test［C］∥International Congress and Exposition.Detroit，Michigan：SAE International，1998：22－35.

［9］ Cepona G，Maninb L，Boltezar M.Experimental identification of the contact parameters between a V－ribbed belt and a pulley［J］.Mechanism and Machine Theory，2010，45（10）：1424－1433.

［10］Chen Liqun.Advance in analysis of vibrations of serpentine belt drive systems［J］.Journal of Mechanics in Engineering，2001，23（4）：8－12.

［11］劳耀新，侯之超，吕振华.发动机前端附件带传动系统频率灵敏度分析［J］.汽车工程，2006，28（5）：477－486.Lao Yaoxin，Hou Zhichao，LüZhenhua.Frequency sensitivity analysis on belt drive system for front end accessories of engine［J］.Automotive Engineering，2006，28（5）：477－486.（in Chinese）

［12］Hou Zhichao，Lao Yaoxin，Lu Zhenhua.Sensitivity analysis and parameter optimization for vibration reduction of undamped multi－ribbed belt drive systems［J］.Journal of Sound and Vibration，2008，317（3）：591－607.

［13］王红云，上官文斌，张少飞.阻尼多楔带传动系统建模及带滑移控制分析［J］.振动、测试与诊断，2011，31（1）：59－63.Wang Hongyun，Shangguan Wenbin，Zhang Shaofei.Model construction of serpentine belt drive systems with multi－ribbed belt damping and belt slipping control［J］.Journal of Vibration，Measurement ＆ Diagnosis，2011，31（1）：59－63.（in Chinese）

［14］Song Guiyong，Shen Yuelin，Chandrashekhara K，et al.Thermal－mechanical finite element analysis of vribbed belt drive operation［C］∥SAE 2003World Congress and Exhibition.Detroit，Michigan：SAE International，2003：1－13.

［15］Shangguan Wenbin，Lu Zhenhua.Experimental study and simulation of a hydraulic engine mount with fully coupled fluid structure interaction finite element analysis model［J］.Computers ＆Structures，2004，82（22）：1751－1771.