分段线性随机共振系统的图像复原应用研究

(杭州电子科技大学计算机学院，浙江 杭州310018)

0 引 言

随机共振的概念是由意大利学者在研究古气象冰川问题时最早提出的[1]。当输入信号、噪声和非线性系统之间存在某种匹配时，一部分噪声能量能够转化为信号能量，从而提高了系统的输出信噪比。随机共振技术打破了只能通过消除噪声来增强信号的传统观念，在弱信号检测中得到广泛应用[2]，并已逐渐延伸到数字图像处理领域[3]。例如，添加适当强度的噪声能使含噪图像具有最佳视觉效果[4];以图像直方图为参照，通过调整双稳系统的参数实现含噪图像复原[5]。这些都为图像的滤波复原提供了新思路。目前，基于随机共振的含噪图像去噪方法研究大多是基于双稳态系统的[6，7]，而且是经过一次随机共振处理。为进一步研究随机共振(Stochastic Resonance，SR)在含噪图像复原中作用，本文以分段线性随机共振系统为图像信号处理器和灰度图像为研究对象，提出级联随机共振的图像复原方法。仿真结果表明，方法能有效的去除图像中的噪声，为图像复原又提供了一种新思路。

1 分段线性随机共振系统

分段线性随机共振系统模型的势函数，由分段方程描述如下:

式中，a、b、c为系统参数，且a ＞b ＞0，c ＞0。

势函数 U (x)的图形如图1所示。它是一个由4条直线构成的分段线性函数，左右两外侧线段与横坐标轴交与x= ±a。阱底位于x= ±b 处，势垒高度ΔU=c。若分段线性系统有信号与噪声共同作用，

式1可以改写为:

式中，S (t)是输入信号，S (t)=H (t)+η(t)，其中 H (t)为输入信号，η(t)是高斯白噪声。η(t) 满足〈η(t) 〉=0，〈η(t) η(0) 〉=2Dδ(t)，其中D表示噪声强度，δ(t)表示冲击函数。非周期信号的仿真如图2所示，从图2(c)的输出波形可以看出分段线性系统能够很好的复原被噪声污染的非周期信号，这也是将它应用于含噪灰度图像复原的理论基础。

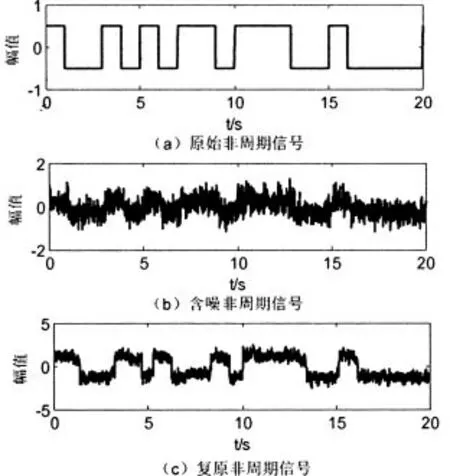
图2 分段线性系统的非周期响应

2 灰度图像复原方法

2.1 级联SR 原理

根据线性响应理论或者绝热近似理论，系统的输入必须满足小参数要求。由于含噪二维灰度图像的灰度值范围是[0，255]，且分段线性系统要求输入信号为双极性信号，因此，将含噪灰度图像的象素取值范围映射到[-0.5，0.5]。这种映射既满足随机共振的小参数要求，又不会使图像信息丢失。

图像级联SR 处理的基本原理过程如图3所示，实质上它是由连续两次SR 实现的。其步骤是:(1)对二维含噪灰度图像按行扫描得到一维序列，然后再对其归一并减去0.5 处理，将其映射到[-0.5，0.5]范围，作为分段线性系统的输入信号;(2)经过分段线性SR 后，一维输出信号其范围有很大改变，则线性变换到[0，1]范围后并恢复成二维矩阵;(3)将步骤2 得到二维矩阵，再按列进行扫描并映射到[-0.5，0.5]范围，再次输入分段线性系统;(4)将步骤3所得的一维序列按步骤2 进行处理，即得到复原图像。

图3 图像级联SR 基本原理框图

2.2 评价方法

可以用信噪比改善因子R 作为图像复原效果的定量评价指标，单位为dB，定义为:

式中，图像的大小表示为N 行和M列，Ii，j表示原始图像第i行第j列象素的灰度值，Ji，j表示含噪图像第i行第j列象素的灰度值，Pi，j表示复原图像第i行第j列象素的灰度值。R为负值时表明复原后含噪图像中的噪声被抑制，R值越小表示复原效果越好。

3 实验结果与分析

3.1 图像级联SR仿真

含噪灰度图像是二维分布的信息，将其灰度值进行降维处理映射到[-0.5，0.5]范围的一维序列，实质也是一个一般的非周期信号，因此本文将通过仿真来考察级联SR 方法对图像及其一维信息的影响。系统参数a=2，b=1，c=0.5，级联SR的数值仿真采用四阶龙格库塔法，仿真图是经典Lena 图，其象素是256×256。

无噪图像的一次SR 结果与一维局部信号如图4所示。图4(a)是原始无噪图，图4(b)是无噪图像的一次SR 结果，图4(c)、(d)分别是图4(a)、(b)的二维灰度图像信号按列扫描后取第5 000-6 000的点。从图4可以看出，一次SR 处理后，图像所含的信息量并没有减少丢失。无噪图像的级联SR与一次SR 结果类似，这里不再给出级联SR的图像。

图4 无噪图像的一次SR 结果与一维局部信号

当Lena 图含有均值为0、方差为0.05的高斯噪声时，其处理的结果如图5所示，图5(a)是含噪图像，图5(b)是含噪图像的一次SR 结果，图5(c)是含噪图像的两次含噪图像结果，图5(d)、(e)、(f)分别是图5(a)、(b)、(c)的二维灰度图像信号按列扫描后取的第5 000-6 000的点。由图5可以看出，SR可以有效滤除图像中的噪声，使图像变得清晰，而且比较图5(b)、(c)可知，级联SR 处理图像比一次SR 处理图像噪声量明显减少，具有更清晰的效果，有更好的图像输出质量。因此级联SR 比一次SR具有更好的滤除噪声的效果。

图5 含噪图像的一次SR 结果与级联SR 结果

3.2 图像复原效果

为进一步考察级联SR 方法复原含噪灰度图像的效果，对4幅经典图像分别添加不同方差的噪声(固定噪声均值为0)作为原始噪声图像，然后分别使用分段线性系统和经典的双稳系统进行处理，分别计算它们的信噪比改善因子，如表1所示。通过量化比较可以看出，与双稳系统相比，在相同的噪声强度下，分段线性系统去噪效果要稍微好些，且随着噪声的增强，两者去噪效果也都越来越好，这也表明了级联SR 方法是有效可行的。

表1 级联SR 方法在不同噪声下的信噪比改善因子

4 结束语

本文基于分段线性系统模型上的非周期随机共振原理，提出了一种级联SR 方法来处理被噪声污染的灰度图像。为评价级联SR 方法处理含噪图像的效果，把图像的一维信号和信噪比改善因子作为评价指标。实验和分析结果表明，级联SR 复原方法能有效降低图像中的噪声量，从而提高图像的质量。下一步的工作针对实现参数的最优化问题进行进一步的研究探讨。

[1]Benzi R，Sutera A，Vulpiana A.The Mechanism of Stochastic Resonance[J].Journal of Physics A，1981，14(11):453-457.

[2]何大海，赵文礼，梅晓俊.基于随机共振原理的微弱信号检测与应用[J].机电工程，2008，25(4):71-74.

[3]陈可，范影乐，李轶.双稳随机共振机制及其在图像复原中的应用[J].中国图像图形学报，2011，16(7):1 170-1 177.

[4]Marks II R J，Thompson B，EI-Sharkawi，etal.Stochastic resonance of a threshold detector:Image visualization and explanation[J].IEEE International Symposium on Circuits and Systems，2002，(4):521-523.

[5]Ye Qing-hua，Huang Hai-ning，Zhang Chun-hua.Image enhancement using stochastic resonance[A].In Proceedings of International Conference on Image Processing[C].Pniladelphia:Singapore，2004:263-266.

[6]庞全，钱诚，杨翠容，等.基于双稳态随机共振的图像复原技术研究[J].中国图像图形学报，2008，8(13):1 447-1 453.

[7]Leng Yong-gang，Zhao Er-hua，Shi Peng，etal.Image Processing on Two-Dimensional Stochastic Resonance of Parameter-Tuning[J].Journal of Tianjin University，2011，44(10):907-913.