一种鲁棒的三维网格模型盲水印算法

(杭州电子科技大学图形图像研究所，浙江 杭州310018)

0 引 言

随着多媒体技术的发展，数字媒体的应用也越来越广泛，而伴随着这些应用的同时，数字产品的盗用、篡改等侵权等问题也一并出现。数字水印作为一种技术手段，可以有效保护数字产品的版权[1]。目前，图像数字水印和音频视频数字的研究比较多，三维网格模型自身的这些特点和对其攻击方式的多样性导致了其嵌入和提取水印比较复杂。按照水印的工作域来看，现在三维模型水印算法主要分为空域水印算法和频域水印算法[2]。3D 网格模型算法[3，4]最早有两种算法，其中包括修改模型几何属性的TSQ 水印算法和TVR算法，但它们都对网格简化和噪声等攻击不具有鲁棒性。在这之后又相继出现了AIE算法[5，6]和三角形束算法[7]等。还有研究者提出了一些频域水印算法[8，9]，对网格简化、噪声、剪切以及它们的混合攻击具有鲁棒性。比如基于小波变换的三维网格模型水印嵌入算法[10]，基于球面参数化和多分辨率技术的水印算法[11，12]。但是这些频域算法大多数在检测水印时需要对待测网格模型进行重采样、网格对齐等预处理来完成检测，使得算法的实用性不强。文献13 提出的三维网格盲水印算法在提取水印时不需要原始网格也不需要对网格进行校准等预处理，利用了傅里叶变换的加法和乘法性质，对平移及均匀缩放操作具有良好的鲁棒性，但是它对旋转操作及顶点重排序攻击不具备抵抗性。本文提出的水印算法在文献13算法的基础上加以改进，使得算法对旋转、平移和均匀缩放具有较好的鲁棒性。

1 算法基本原理

文献13是将水印信息添加到几何坐标中，但是几何坐标中的水印信息鲁棒性差，容易受到攻击而被抹去。本文的算法是将模型顶点按照一些特征进行排序，确保模型仿射变换前后顶点排序不变，然后将水印信息藏到其纹理坐标中。对于没有纹理坐标的三维模型，可以自己手动添加纹理坐标，这并不会对三维网格模型造成影响。

其中，模型顶点排序特征选取具体为模型中心到模型顶点的距离，模型顶点与它的一阶邻域中心点以及模型中心点3点连线的夹角这两个全局几何特征来决定顶点的唯一排序，如图1所示(顶点与中心点连线和弧度)。这里选取的两个几何特征都是较稳定的全局几何特征，不会因为模型的仿射攻击而发生变化。其中假设P=(V，T)表示一个三角形网格模型，其中V ={Vi|i∈(1，N)}表示模型中的顶点，N为模型顶点的数目。T表示模型的拓扑关系。从T 中可以得到每个顶点的1 阶邻域.对于顶点Vi，其一阶邻域定义为所有与之相连接的顶点集合，如图2所示(黑色顶点(除Vi)的集合):

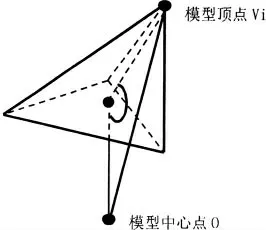
图1 顶点Vi的距离Si和Vi 对应的夹角θi

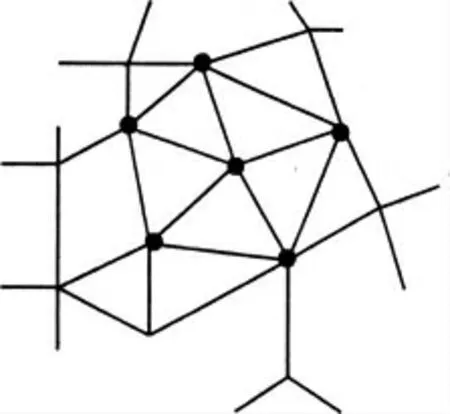
图2 Vi的1 阶邻域

另外，为了得到一个唯一不变的的顶点序列，本文首先计算模型的中心点坐标O，每个点Vi到模型中心的距离Si，然后再计算每个点的一阶邻域的中心Ti，再计算向量TiO和TiVi的夹角θi。将模型顶点先按Si的大小升序排列，如果Si相同，再按照对应的θi来进行排序，最终获得一个唯一的顶点序列，最后，选取顶点序列的一部分，将水印数据添加到顶点的纹理坐标中。其中水印信息来自于基于傅里叶变换的图像水印算法，即首先将原始水印嵌入一个稳定图像中，然后将嵌入水印的图像和原始图像相减得到水印信息。

1.1 水印嵌入过程

嵌入过程如图3所示:

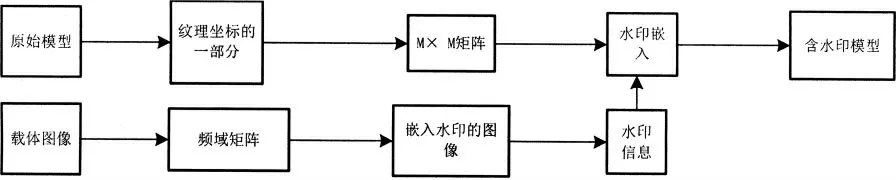
图3 水印嵌入流程

步骤如下:

(1)计算网格模型每个顶点到模型中心的距离Si和其对应的夹角θi。对原始三维网格模型的顶点序列按照上述方法进行排序，得到一个唯一的三维网格顶点序列;

(2)利用图像水印算法得到水印信息W'。和文献13的方法是略有不同，这里将一幅m×m的二值图像作为原始水印添加到经过傅里叶变换后的M×M 大小的灰度载体图像I的中频部分，反变换回来后得到嵌入水印的图像I'。通过加法公式得到最终要嵌入三维网格模型的水印信息W'。水印信息可能需要略作调整，调整后W(i，j)＞0，以便添加到三维网格模型中;W'(i，j)=I'(i，j)-I(i，j)+δi∈(1，m)，j∈(1，m)，δ是一个大于0的整数;

(3)选取排序后顶点序列前M×M个顶点，将水印信息W'添加到排序后的顶点的纹理坐标。这里是将水印信息替换掉纹理坐标值的5-7 这3个有效位，这样既保证了水印嵌入的完整性又具有很好的透明性。这样就完成了水印嵌入的整个过程。

1.2 水印提取过程

水印提取基本可以看作嵌入过程的逆过程，本文算法提取水印前不需要进行网格矫正重采样等预处理，也不需要原始网格:

(1)计算待检测模型每个顶点到模型中心的距离T和其对应的夹角θi;

(2)同样的，按照上述方法对模型的顶点进行排序，得到唯一的三维网格序列;

(3)选取排序后序列的前M×M个顶点，提取纹理坐标的5-7的3个有效位，即为水印信息;

(4)将得到的水印信息组成m×m的矩阵，进行傅里叶变换，按照嵌入过程中的图像水印算法提取出最终的水印。

2 仿真实验

为验证本文提出的算法的鲁棒性和不可见性，本文做了仿真实验，这里选取2个模型，如图4(a)、(e)所示:含纹理坐标的a模型和不含纹理坐标的b模型，其中模型a 含有15 645个顶点、30 860个三角面，模型b 含有21 099个顶点、20 904个三角面。如图4所示，原始模型a、b和它们分别嵌入水印后的模型以及受到旋转和缩放攻击后的模型如下。通过实验可以看出，算法的透明性比较好，嵌入了水印后的模型失真度很低，这是因为水印是嵌在了模型的纹理坐标的低位有效位，对模型的影响很小。为了验证算法的鲁棒性，对嵌入水印后的模型进行仿射变换(旋转、平移、均匀缩放)攻击，测试结果如表1所示。表1的测试结果表明，算法能够抵抗模型的仿射变换攻击，这是因为模型嵌入水印时，找到了两个抗仿射变换的几何特征用来帮助顶点排序，构成了模型顶点的唯一序列。

图4 模型a、b 嵌入水印前后

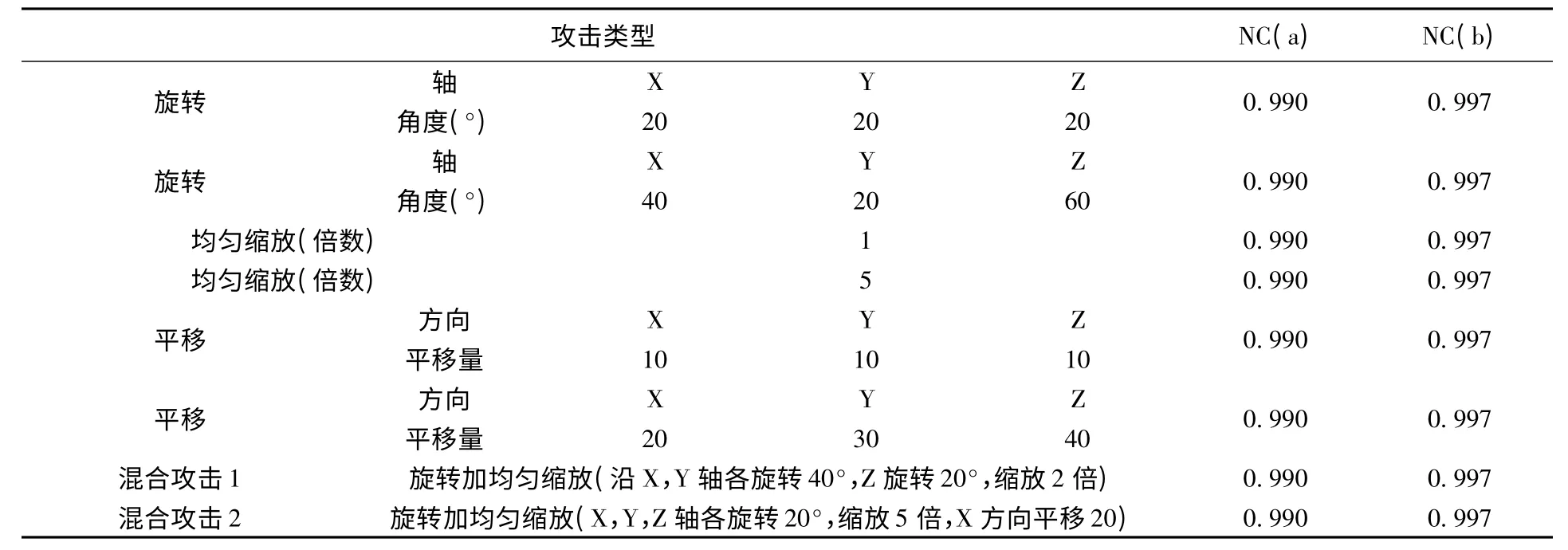
表1 模型a、b 仿射变换攻击实验及实验结果

3 结束语

本文提出了一种改进的三维网格模型水印算法，是将顶点排序然后选取一部分再将水印加到其纹理坐标中。实验结果表面，此水印算法具有不可见性，由于选取了两个稳定且抗仿射变换的全局几何特征用来作为顶点排序的基准，算法对仿射变换攻击具有较好的鲁棒性。

[1]冯小青.三维模型数字水印算法及关键技术研究[D].杭州:浙江大学，2009.

[2]潘志庚，孙树森，李黎.三维模型数字水印综述[J].计算机辅助设计与图形学学报，2006，8(14):1 103-1 110.

[3]Ohbuchi R，Masuda H，Aono M.Watermarking three-dimensional polygonal models through geometric and topological modifications[J].IEEE Journal on Selected Areas in Communication，1998，16(4):551-560.

[4]Ohbuchi R，Masuda H.Watermarking three-dimensional polygonal models[C].Washington:Proceedings of the ACM International Conference on Multimedia，1997:261-272.

[5]Benedens O，Busch C.Towards blind detection of robust watermarks in polygonal models[C].Interlaken:Proceedings of Euro graphics，2000:199-208.

[6]Benedens O.Affine invariant watermarks for 3D polygonal and NURBS based models[C].Wollongong:Proceedings of the 3rd International Workshop Information Security，2000:15-29.

[7]Benedens O.Two high capacity methods for embedding public watermarks into 3D polygonal models[C].Orlando:Proceedings of the Multimedia and Security-Workshop at ACM Multimedia，1999:95-99.

[8]Harte T，Bors A G.Watermarking 3D models[C].Rochester:Proceedings of IEEE International Conference on Image Processing，2002:661-664.

[9]刘旺，孙圣和.基于DFT的鲁棒三维网格模型数字水印算法[J].计算机工程与应用，2005，14(5):192-197.

[10]Kanai S，Date H，Kishinami T.Digital watermarking for 3D polygons using multi-resolution wavelet decomposition[C].Tokyo:Proceedings of International Workshop on Geometric Modeling，1998:296-307.

[11]Yin K K，Pan Z G，Shi J Y，etal.Robust mesh watermarking based on multi resolution processing[J].Computers ＆Graphics，2001，25(3):409-420.

[12]Li L，Zhang D，Pan Z，etal.Watermarking 3D mesh by spherical parameterization[J].Computers ＆ Graphics，2004，28(6):981-989.

[13]李黎.数字图像和三维几何模型水印技术研究[D].杭州:浙江大学，2004.