高温后混凝土断裂韧度及其权函数计算法
2013-12-02俞可权商兴艳陆洲导
俞可权,商兴艳,陆洲导
(同济大学 土木工程学院,上海200092)
1976年Hillerborg提出了虚拟裂缝模型[1],该模型认为可将混凝土裂缝端部的微裂缝区视为一虚拟的可传递应力的裂缝,缝上各点传递应力的大小根据该点变形值而定.在Hillerborg研究基础上,Bazant提出了钝裂缝带模型(CBM)[2].20世纪80年代以来,以虚拟裂缝模型FCM 和断裂带模型CBM 为基础的混凝土非线性断裂力学取得了迅速的发展,许多反映裂缝扩展以及断裂过程区(FPZ)的模型也相继建立起来,主要有双参数模型(TPFM)[3],有效裂缝模型(ECM)[4],尺寸效应模型(SEM)[5].
上述各类断裂模型中,均以临界断裂韧度作为单一参量,在此基础上,徐世烺等[6-8]观察了混凝土材料裂缝发展的全过程,提出了双K(开裂韧度和失稳韧度)断裂模型及其断裂控制参数的闭合积分解析解,随后提出了实用的简化计算公式,并使用三点弯曲梁和楔入劈拉试件验证了简化公式的合理性.张秀芳等[9]采用权函数法计算黏聚断裂韧度的计算公式,计算混凝土双K断裂韧度,发现其与积分法计算的黏聚韧度具有很好的吻合性.
在常温混凝土断裂性能研究的基础上,众多学者对高温后混凝土的断裂性能也进行了广泛研究,且多集中于材料断裂能方面[10-12],对断裂韧度的研究开展较少[13-14],在研究中未考虑裂缝的亚临界扩展,其计算结果值得商榷.
本文采用楔入劈拉法试件,研究高温后混凝土断裂性能,确定混凝土在各温度下的开裂韧度KiniIc和失稳韧度KunIc,采用Petersson双线性软化曲线计算黏聚韧度,并通过权函数法进行进一步验证,以期对双K断裂模型在高温后混凝土的适用性进行论证.
1 积分法计算高温后混凝土黏聚断裂韧度
黏聚韧度由虚拟裂缝上的黏聚应力积分得到,黏聚应力的不同分布将对临界黏聚韧度KcIc的计算造成直接影响.本文采用Petersson双线性软化曲线来确定高温后混凝土黏聚断裂韧度,其具体形式如下:

式中:σs为双线性软化曲线转折点处应力;ft为高温后混凝土抗拉强度;ws为双线性软化曲线转折点对应的张开位移;GF为高温后混凝土断裂能;w0为黏聚力为零处的裂缝张开宽度.
在文献[15]的分析中,指出对于小尺寸试件而言,当达到最大荷载时,临界裂缝尖端张开位移μc 不大于双线性软化曲线转折点对应的张开位移,即μc≤ws(图1a),因此用单线性函数来计算临界黏聚韧度的大小;但是对于大尺寸试件,μc 则明显大于ws(图1b),此时应用双线性函数计算临界黏聚韧度值.
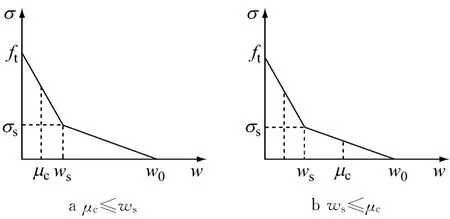
图1 临界裂缝尖端张开位移μc 与软化曲线转折点位移ws 的关系Fig.1 Relationship between critical crack tip opening displacement μc and softening curve turning point displacement ws
本文采用的楔入劈拉法试件虽然尺寸较小,但历经高温后,试件延性增加,μc 值有可能大于式(1)提及的转折点张开位移ws,故在计算黏聚韧度值时考虑以下两种情形:
(1)裂缝失稳前,黏聚应力近似呈线性分布(图2a),在临界等效裂缝开口位移ac范围内,任意等效裂缝位置x处的黏聚应力为
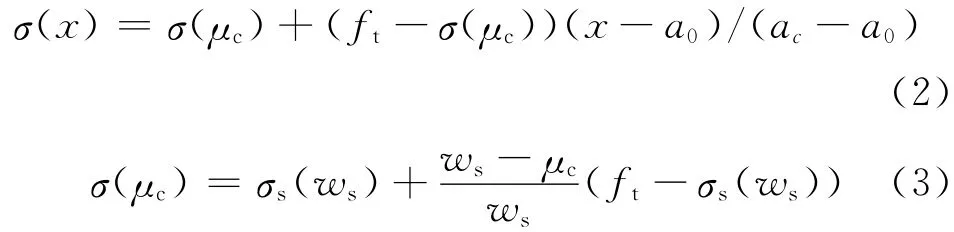
式(2),(3)中:σ(μc)为临界状态下预制缝端(x=a0,a0为裂缝预制长度)开口位移达到μc 时的黏聚力;σs(ws)为软化曲线转折点处应力;ac为临界裂缝开口位移.
临界黏聚韧度KcIc可采用下式计算[16]:
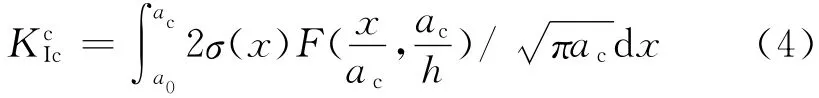
(2)裂缝失稳前,当黏聚力如图2b所示时,其黏聚力表达式如下:
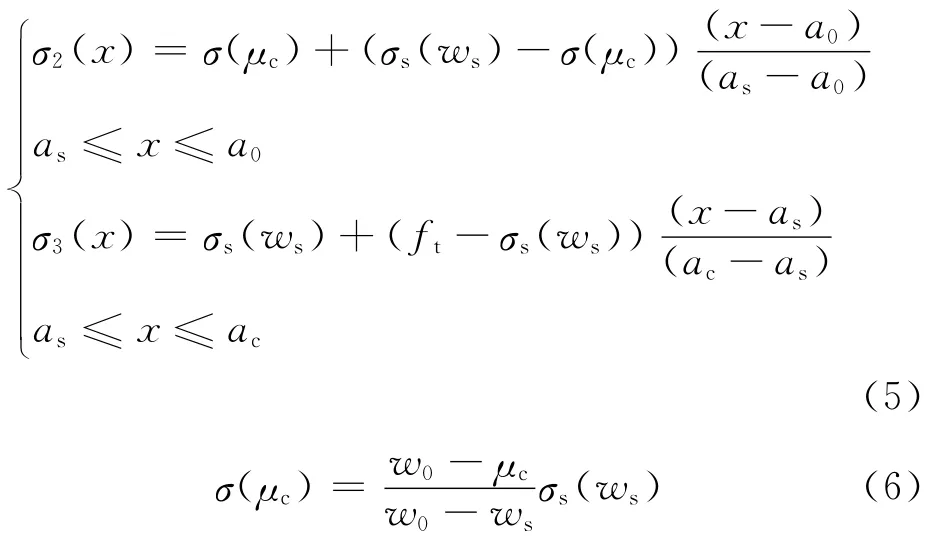
式中:as为裂缝张开口位移等于ws时对应的等效裂缝长度,求解非线性方程就可获得等效裂缝长度as[3].

式中:δc为裂缝开口位移.
此时,黏聚韧度通过下式计算:


图2 裂缝失稳前黏聚应力分布情况Fig.2 Distribution of cohesive stress before unstable crack propayation
2 权函数法计算混凝土黏聚断裂韧度
为进一步验证上述黏聚韧度公式计算的准确性,本文继续采用权函数方法计算临界黏聚韧度.
(1)当μc≤ws时,对应的黏聚应力分布见图2a,根据文献[17]计算得到采用四项权函数的黏聚韧度表达式为
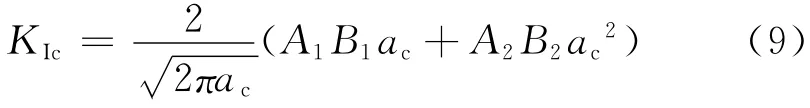
具体公式参见文献[17].
(2)当w0>μc>ws时,对应的黏聚应力分布见图2b,采用四项权函数形式,得到黏聚韧度表达式为
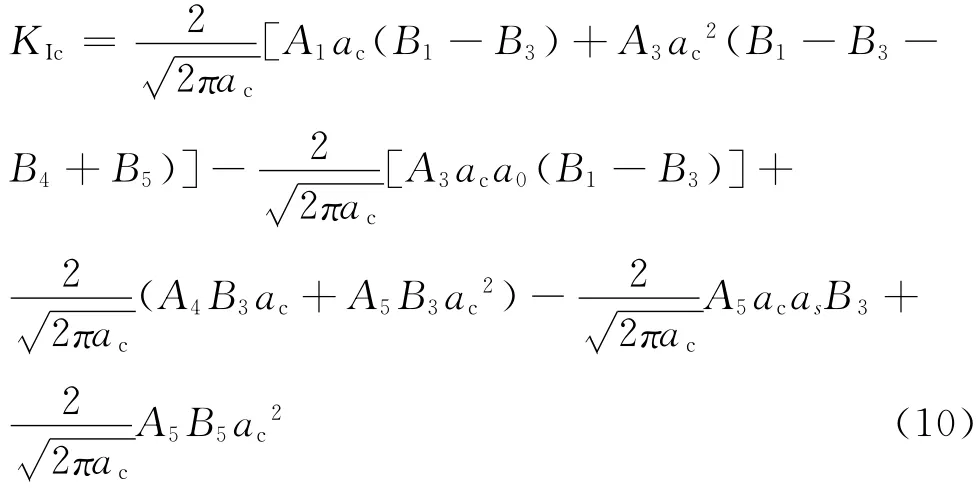
3 双K 断裂韧度的计算[7]
3.1 临界有效裂缝长度ac
对于高温后混凝土试件,仍然根据线弹性渐进叠加假定,非线性的断裂过程可简化为一系列的线性叠加过程.当外荷载达到最大值Pmax时,裂缝开口位移δc也达到最大,裂缝长度从预制长度a0发展到临界有效裂缝ac.从实测的荷载—位移(P-δ)曲线上读取Pmax和临界裂缝张开位移δc,代入式(5),即可得临界有效裂缝长度ac.

式中:h为楔入劈拉试件高度;h0为裂缝张口处刀口厚度;δc为高温后试件临界裂缝张开口位移;E为弹性模量;t为试件厚度;Pmax为峰值荷载.
3.2 起裂韧度与失稳韧度
根据线弹性渐进叠加假定,起裂断裂韧度与失稳断裂韧度的计算仍可采用线弹性断裂力学中的公式.将试验测得的起裂荷载Pini,a0,Pmax和计算得到的ac代入下式,可得失稳韧度

式中:f(α)为试件形状参数,具体公式参见文献[7].
根据双K断裂韧度理论,起裂韧度失稳韧度和黏聚韧度三者之间的定量关系为

考虑到混凝土在历经高温后的起裂韧度相对失稳韧度较小(600 ℃时两者比值为1/5),对于高温后混凝土主要考虑其失稳韧度.本文中,将实测失稳断裂韧度记为,将由积分与权函数计算得到的失稳断裂韧度记为
4 试验验证与结果分析
采用楔入劈拉试验对权函数法和积分法两种方法确定的双K断裂韧度进行比较.楔入劈拉试件尺寸统一采用230mm×200mm×200mm,预制开口裂缝高80 mm,厚3 mm,试件形式详见图3(图中b=200 mm,d=65 mm,h=200 mm,f=30 mm,a0=80mm,θ=15°).试件混凝土配比(质量比)为水泥∶砂∶石子∶水=1∶3.44∶4.39∶0.8,粗骨料最大粒径为16mm,标准配合强度为C30.每个试件内预制裂缝附近均插有热电偶,深入试件深度为100 mm,以测得试件中心温度.试件自然洒水养护60d后,采用300mm×300mm×900mm 的电炉对混凝土试块进行加热,历经65,120,200,300,350,400,450,500和600 ℃高温.试件加热至65,300,450,600 ℃的平均耗时为50,182,294,453 min.试件冷却后采用塑料袋密封减少环境湿气渗入.
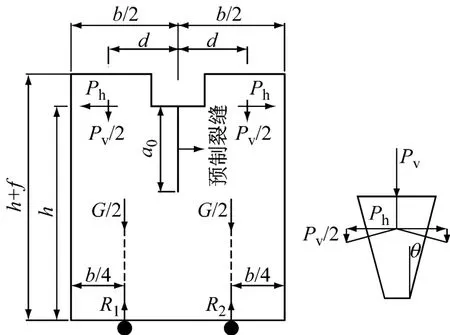
图3 试件几何形式Fig.3 The geometry of specimens
图4描述了各温度下试件的竖向荷载Pv和裂缝开口位移δc之间的关系,随着温度的上升,极限荷载持续下降,而对应的开口位移则明显增加,试件表现出明显的延性.
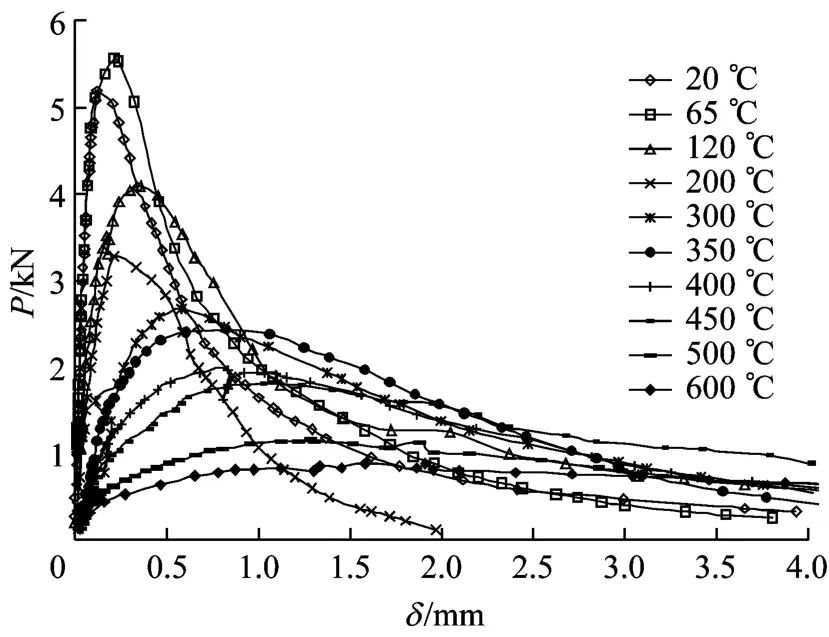
图4 各温度下典型试件的P-δ 曲线Fig.4 P-δcurves of specimens at different temperatures
表1 列出了试验的原始数据,包括起始荷载Pini,临界荷载Pmax及其对应裂缝开口位移δc,弹性模量E,断裂能GF,起裂韧度及实测失稳断裂韧度起裂荷载Pini采用荷载—裂缝开口位移曲线中转折点进行确定,同时利用转折点前曲线的初始柔度,参照文献[7]的公式计算弹性模量E.由积分法计算得到的黏聚断裂韧度及失稳断裂韧度由权函数法计算得到的黏聚断裂韧度及失稳断裂韧度也列入表1.
由表1可知,在总共45个有效试件中,当采用积分法计算时,计算失稳韧度与实测失稳韧度的误差在5%以内的试件共有22个,占49%,误差在15%以内的试件共40个,占89%;当采用权函数法计算时,计算失稳韧度Kun-wfIc与实测失稳韧度Kun-EIc的误差在5%以内的试件共有20个,占45%,误差在15%以内的试件共42个,占93%,表明双K断裂模型适用于高温后混凝土断裂性能的描述;积分法与权函数法计算的黏聚韧度的误差在5%以内的试件占65%,显示出两者具有很好的吻合性.

表1 不同方法计算的混凝土失稳韧度值的比较Tab.1 Comparison of unstable fracture toughness determined by weight function approach and analytical approach
5 结论
本文采用楔入劈拉法对高温后混凝土的断裂性能进行研究,设置20~600 ℃共10组温度,在总共45个有效试件中,计算失稳韧度Kun-IIc与实测失稳韧度Kun-EIc的误差完全在工程可控范围内,由此论证了双K断裂准则对于高温后混凝土的适用性.在此基础上,进一步运用权函数法对黏聚韧度进行计算并与积分法计算值进行比较,两者误差较小,具有很好的吻合性,权函数法具有较高的计算精度.
[1] Hillerborg A,Modeer M,Petersson P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements [J].Cement and Concrete Research,1976,6(6):773.
[2] Bazant Z P,Oh B-H.Crack band theory for fracture of concrete[J].Materials and Structures(RILEM),1983,16(93):155.
[3] Jenq Y S,Shah S P.Two parameter fracture model for concrete[J].Journal of Engineering Mechanics,1985,111(10):1227.
[4] Nallathambi P,Karihaloo B L.Determination of specimen-size independent fracture toughness of plain concrete[J].Magazine of Concrete Research,1986,38(135):67.
[5] Size effect in blunt fracture:concrete,rock,metal[J].Journal of Engineering Mechanics,1983,110(4):518.
[6] 徐世烺.混凝土断裂机理[D].大连:大连理工大学土木工程学院,1988.XU Shilang.Fracture mechanism of concrete [D].Dalian:College of Civil Engineering of Dalian University of Technology,1988.
[7] Xu S L,Reinhardt H W.Determination of double-Kcriterion for crack propagation in quasi-brittle fracture,Part I,II,III[J].International Journal of Fracture,1999,98(2):111.
[8] Xu S L,Reinhardt H W.A simplified method for determining double-Kfracture parameters for three-point bending tests[J].International Journal of Fracture,2000,104(2):181.
[9] 张秀芳,徐世烺.权函数法计算的混凝土断裂韧度[J].工程力学,2011,28(4):58.ZHANG Xiufang,XU Shilang.Fracture toughness of concrete determined using weight function approach [J].Engineering Mechanics,2011,28(4):58.
[10] Baker G.The effect of exposure to elevated temperatures on the fracture energy of plain concrete[J].Materials and Structures,1996,29(190):383.
[11] Zhang B,Bicanic N,Pearce C J,et al.Residual fracture properties of normal-and high-strength concrete subject to elevated temperatures [J].Magazine of Concrete Research,2000,52(2):123.
[12] Nielsen C V,Bicanic N.Residual fracture energy of highperformance and normal concrete subject to high temperatures[J].Materials and Structures,2003,36(262),515.
[13] Hisham Abdel-Fattah,Hanoush A S.Variation of the fracture toughness of concrete with temperature [J].Construction Building and Materials,1997,11(2):105.
[14] Prokopski G.Fracture toughness of concretes at high temperature[J].Journal of Materials Science,1995,30:1609.
[15] XU S.Determination of parameters in the Bilinear,Reinhardt’s and exponentially nonlinear softening curves and their physical meanings[C]//Werkstoffe und Werkstoffprufung im Bauwesen.Hamburg:Libri BOD,1999:410-424.
[16] 中国航空研究院.应力强度因子手册[M].北京:科学出版社,1981.Aviation Institute of China.Stress intensity factor handbook[M].Beijing:Science Press,1981.
[17] Kumar S,Barai S V.Determination the double-Kfracture parameters for compact tension and wedge splitting tests using weight function [J].Engineering Fracture Mechanics,2009,76:935.
