MULTI-OBJECTIVE PROGRAMMING FOR AIRPORT GATE REASSIGNMENT
2013-12-02LiJunhui李军会ChenXin陈欣ZhuJinfu朱金福
Li Junhui(李军会),Chen Xin(陈欣),Zhu Jinfu(朱金福)
(1.College of Economics and Management,Nanjing University of Aeronautics and Astronautics,Nanjing,210016,P.R.China;2.Guangdong Airport Management Company,Guangzhou,510406,P.R.China;3.Traffic College,Southeast University,Nanjing,210010,P.R.China)
INTRODUCTION
Airport gate assignment is the process of assigning right airport gates for flights in order to meet corresponding requirements,but the airport gate assignment must be under some constraints.Efficient gate assignment has an important significance on improving the utilization rate of airport gates,reducing flight delays,facilitating airline passengers,enhancing airport security ability,and so on.Proceeding from passengers′satisfaction maximization and walking distance minimization,domestic and overseas scholars have set up 0-1programming[1]and integer programming model[2],worked out by branch and bound method and heuristic algorithm respectively.Xu and Bailey[3]took passengers′turnaround time mini-mization as objective to set up model.Yan and Huo[4]established multi-objective 0-1programming model concerning the shortest passengers′walking distance and waiting time.As an NP problem,the gate assignment algorithm has been improved by some related research[5-7].
Planned assignment is the course of assigning gates according to certain information (flight schedule).In fact,there is certain randomness,including flight uncertainty (early arrived,delayed,cancellation,alternate,etc.),emergency cases(the long delay of departure flight which occupies a gate,the gate is unavailable because of equipment failure,etc.),and so on.When the above events occur,it is necessary to adjust the planned assignment to solve the problem of gate reassignment.In general,the assumption that the number and time distribution of flights remains in the scope of airport capacity and airport gates are sufficient to provide services for the same-day flights to match the actual situation[8].Based on this assumption,Zhu Shiqun[9]considered flight uncertainty and took the shortest transferring distance of related people caused by gate changes as objective to set up agate reassignment model,and good results were achieved.But he did not consider the arrival and transit passengers,and also did not take the emergency cases into account.In emergency cases,the assumption no longer holds,because in a certain period of time,the reduction of the total number of gates may lead to delays of arrival flights.For minimizing the total flight delays, Gu and Chung[10]established a gate reassignment model which was under perturbations of delayed flights and worked out by genetic algorithm.Yan and Tang[11]minimized the passengers′waiting time and established a gate reassignment model concerning the random flight delays,meanwhile put forward a kind of heuristic algorithm.Refs.[10-11]respectively established single-objective optimization model.But they did not fully reflect either the passengers′demands,or the characteristics of gate reassignment,and the solving process was too complex.
At present,there is less study on gate reassignment,especially in emergency cases;therefore, this aspect needs to be further researched[12-13].Based on the above research and combining with the concept of disruption management represented in Ref.[8],this paper proposes a multi-objective programming model applied to emergency situation.This model minimizes the total time of flight delays,the total passengers′walking distance and the number of flights reassigned to other gates different from the planned ones.Finally,an example is given.
1 AIRPORT GATE REASSIGNMENT MODEL
According to the concept of disruption man-agement,Ref.[8]put forward three goals of gate reassignment.
(1)Maximum guarantee of carrying out smoothly ground support activities
It is no doubt that emergency situation will disrupt the normal order of the airport operation.The basic objective of gate reassignment is to make sure the airport ground activities are carried out smoothly.And this objective is the premise and foundation of other objectives.
(2)Making solutions of gate reassignment optimal as far as possible
The planned assignment is the optimal solution for the current working day,but the emergency situation will generally undermine its optimality.The airport services must regard passengers′satisfaction as its purpose,so it is necessary to optimize the solutions of gate reassignment.
(3)Minimizing changes of original assignment as far as possible
If the number of flights reassigned to other gates different from the planned ones is too large,it will increase the load on the staff,and even make the operation of the airport chaos.
Based on the three above objectives,this paper proposes several objectives of gate reassignment when emergency cases occur.The primary objectives are to ensure that arrival flights reach the gate as soon as possible and to reduce flight delays caused by the shortage of gate resources.The secondary objectives are reducing passengers′walking distance as far as possible,optimizing the solution of gate reassignment,improving airport service quality,and meanwhile,controlling the adjustment of planned assignment.Therefore,this paper takes the total time of flight delays minimization,the passengers′ walking distance minimization and the least change of planned assignment as objective function.
While solving the planned assignment problems that take the total time of flight delays minimization and the passengers′ walking distance minimization as objective function,each flight should be calculated for its objective function value and the solving process is complicated.Ac-cording to the above discussion,in the planned assignment,there are no flight delays caused by capacity constraints,and passengers′walking distance is the optimal solution.The flights in the gate reassignment without making adjustments are absolutely optimal solution because gate reassignment is based on planned assignment,so the process of optimizing the gate reassignment scheme is to work out the optimal solution of flights which are adjusted and this process can be guaranteed to minimize changes of planned assignment at the same time[9].In emergency cases,if a flight which occupies a gate is adjusted,it may affect other flights which are assigned to this same gate and even cause delays,but this will not affect other flights which are assigned to other gates.Thus,the total time minimization of flight delays can be simplified to the shortest total delay of flights which are assigned to the certain gates with flight adjustments.By the same token,passengers′ walking distance minimization can be simplified to the shortest walking distance of passengers whose flights are adjusted.
Suppose that emergency cases occur in the period time of Tand the airport needs to optimize the order of the arrival flights which arrive at the airport in the period time of T.The objective functions(1)and(2)are shown as follows
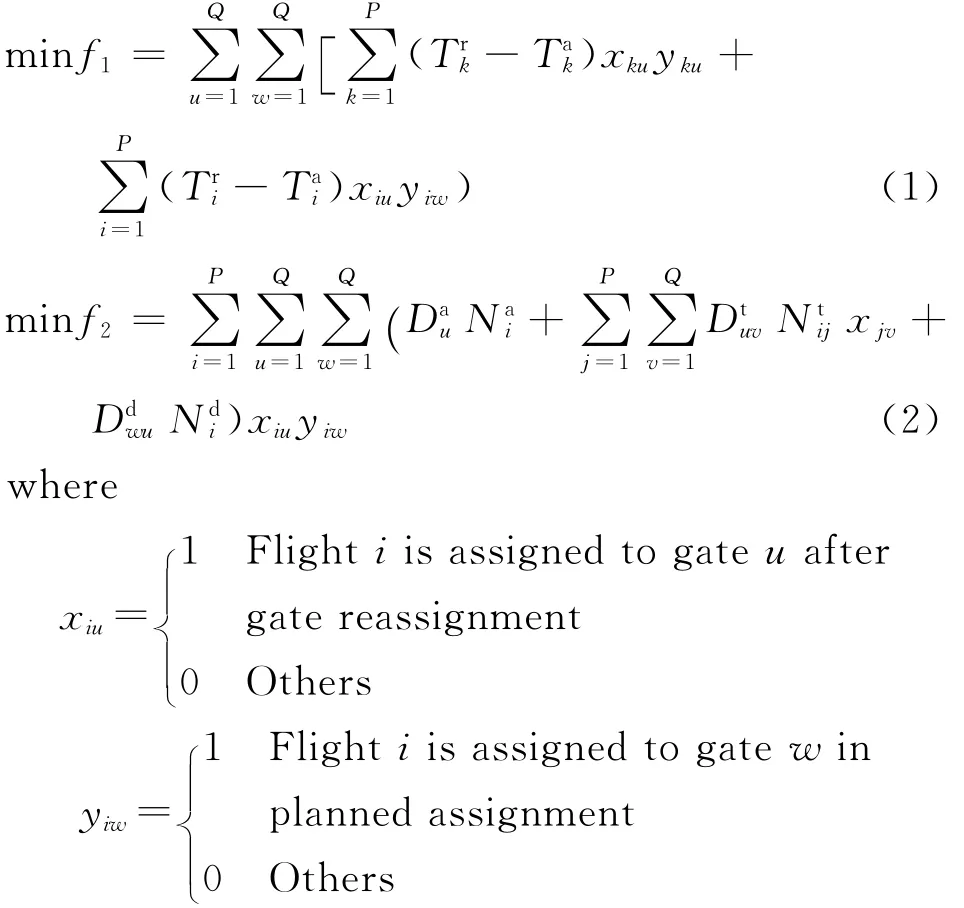
and P,Qrespectively represent the total number of flights and the total number of available gates both in the period time of T,Nai,Ndithe number of arrival passengers and departure passengers of flight i,Nitjrepresents the number of passengers transferring from flight i to flight j,Dauthe distance of arrival passengers moving from gate uto the baggage claim area,Ddwuthe distance of departure passengers transferring from gate wto gate u,Dtuvthe distance of transit passengers transferring from gate uto gate v,Tirthe actual time of flight i reaching the gate,Tiathe expected time of flight i reaching the gate.
To simplify the model and improve its versatility,this study does not consider such constraints as the matching between gate and aircraft type,the special gate and the flight priority.In other words,all the gates can be assigned to any flights.This paper considers basic constraints as follows.
(1)Each flight can only be assigned to one gate,that is
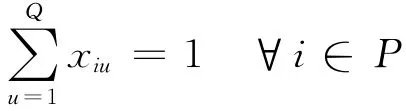
(2)Each gate can only be assigned to one flight,that is
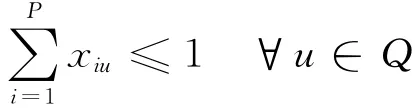
(3)Capacity constraint:The actual time of the flight reaching the gate is not earlier than its expected time,that is
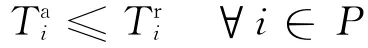
2 ALGORITHMS
Such methods as evaluation function method,objective programming method and interactive programming method are generally used to solve the problems of multi-objective programming.As the objectives of a multi-objective programming model are hard to reach the optimal solutions simultaneously,finding satisfactory solution that depends on the application background is an effective way to solve problems of multi-objective programming.
As mentioned above,reducing flight delays is primary task when emergency occurs,followed by the consideration of the shortest passengers′walking distance.Therefore,in the above multi-objective programming model proposed,the importance of f1is greater than that of f2.This study deems that it can decrease the solution space of f2and the complexity of solving process by setting f1a satisfactory solution threshold according to airport requirements or empirical value,and then working out a satisfactory solution set using simulated annealing algorithm.The next step is to find the optimal solution of f2in the satisfactory solution set and that is the definitely optimal solution of the model.The algorithm is shown as followes.
(1)Initialization
Set that satisfactory solution threshold is fs,satisfactory solution set is F,the initial value is t0,and the iteration index c=0,tc=t0.The selection of initial solution and the setting of initial value are conducted by the following steps.
① Generate free time quantum of all the available gates.[Bul,Sul](l=1,2,3,…)is the first free time quantum of the gate u(u∈Q).
② Considering each flight in M (Mis a collection of all flights which are assigned to unavailable gates in planned assignment),calculate the value of min{|Tai-Bul|},i∈ M,u∈Q .
③ According to the result of step②,generate the initial scheme of gate reassignment.Then,calculate the value of objective function f1,take the result as initial solution,and note it as s0.
④ Considering each flight in M,calculate the value of max= {|Tai-Bul|},i∈ M,u∈Q .
⑤ According to the result of step④,generate the scheme of gate reassignment.Then,calculate the value of objective function f1and note it as s*.
⑥ Obtain the initial value t0=|s*-s0|.
(2)Generation of new solution
While using natural number to code,one solution represents one assignment scheme.For example,[5,10,10,…]represents that flight 1 stops at gate 5,flight 2stops at gate 10and flight 3stops at gate 10.Any position exchange of two numbers can generate a new solution.Randomly generate a neighborhood solution n ∈ N (m)(N(m)represents the neighborhood of m).If the value of objective function f1is smaller than fs,store the neighborhood solution into Fand then calculate the increment of the objective function valueΔf1=f1(n)-f1(m).
(3)Judgment and treatment of new solution
IfΔf1<0,set m=n,and jump to step(4);otherwise generateξ=U(0,1).If expξ,set m=n.
(4)Judgment of inner loop termination criterion
If the thermal equilibrium is reached,namely,the times of inner loops is bigger than g(tc)=P(c+1)(Pis the total number of all flights),jump to step(5);otherwise jump to step(2).
(5)Judgment of outer loop termination criterion
If lower tc,the cooling function is tc+1=tion remains the same after 100consecutive iterations,jump to step (6);otherwise jump to step(2).
(6)Seeking optimal solution of objective function f2
After a search of the above steps,the initial solution space of the model is greatly reduced,meanwhile,the satisfactory solution set Fis obtained.And Fis the feasible solution space of the objective function f2.In the process of seeking the optimal solution of objective function f2,the each value of f2should be calculated firstly,followed by using exhaust algorithm to sort order and look for the result.
3 NUMERICAL EXAMPLE
This study takes the operation of a domestic airport in 11:00—14:00as an example.Flight 13 delays for some reason and it will not take off until 14:00.Gate 11is unavailable caused by malfunction before flight 31arrives.There are 54arrival flights in 11:00—14:00in total.And eight flights that arrive before 11:00will no longer be adjusted.Airport requires that the average delay of arrival flights is no more than 2min.It means that the satisfactory solution threshold fsis 108 min.This study applies the proposed model to optimize gate reassignment for arrival flights.After the calculation of steps(1)-(5),the satisfactory solution set Fconsisting of 68groups of satisfactory solution is obtained.And then,impor-ting the relevant airport gate distance and the number of related airline passengers,the optimal solutions can be calculated by step(6)and the results are shown in Table 1.Because of the huge amount of data,this paper only lists the calculation results,and the operating time in Table 1includes the flight safety time interval.
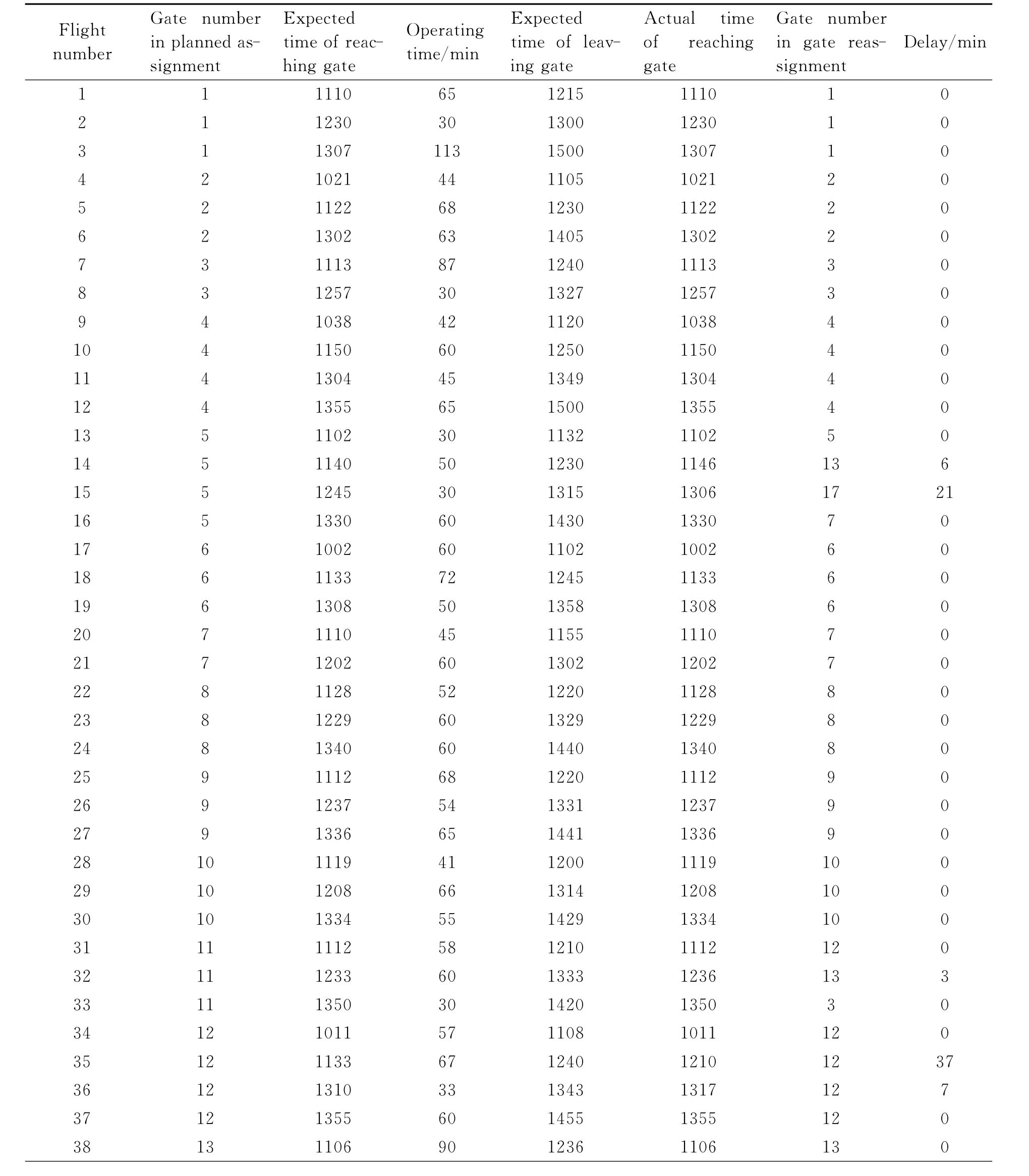
Table 1 Results of gate reassignment

(Continuation)
The total flight delay is 100min and the total passengers′walking distance is 49 265m.This study reassigns gates to six flights whose original gates in planned assignment are unavailable now,while not adjusting gates of other flights.The results show that the change of planned assignment is least by using this model.At the same time,this model fully demonstrates the characteristics of gate reassignment.And it is simple and can be easily solved,in line with the requirements of disruption management.
4 CONCLUSION
In this paper,the problems of gate reassignment in emergency cases are studied,and a multiobjective programming model is established and solved by using simulated annealing algorithm.Considering the interests of passengers and the airport,the model minimizes the total flight delays,the total passengers′walking distance and the number of flights reassigned to other gates different from the planned ones.While using simulated annealing algorithm to solve the model,the initial solution and the initial value are selected according to the characteristics of model,and satisfactory solution threshold is set as well.All of these reduce computational complexity and improve efficiency.Simulation results prove the validity of the model,and the gate assignment solutions obtained meet the requirements of disruption management.
The model proposed in this paper does not consider the impact of cargo and does not fully reflect the randomness of flights.Such aspects as modeling process and algorithm design can be improved.Flight randomness is where the difficulty of gate reassignment lies,and it mainly displays in two aspects:It is difficult to draw its probability distribution;it is difficult to carry out effective prediction.Hence,the research on the random-ness law of flights is of great significance for gate assignment problems.Under the circumstances of unclear flight randomness,the process of planning how to improve the robustness of planned assignment scheme and reduce the difficulty of real-time assignment caused by flight randomness needs to be studied in depth.How to adopt recovery strategy as well as set up reasonable real-time assignment model under the circumstances of perturbations of delayed flights is also the direction of further research.
[1] Babic'O,Teodorovic'D,Tošic'V,et al.Aircraft stand assignment to minimize walking[J].Journal of Transportation Engineering,1984,110(1):55-66.
[2] Mangoubi D F X,Mathaisel R S.Optimizing gate assignments at airport terminals[J].Transportation Science,1985,19(2):173-188.
[3] Xu J,Bailey G.The airport gate assignment problem:Mathematical model and a tabu search algorithm[C]//Proceedings of the 34th Hawaii International Conference on System Sciences.Hawaii,USA:[s.n.],2001:102-111.
[4] Yan Shang-yao,Huo Cheun-ming.Optimization of multiple objective gate assignments[J].Transportation Research Part A,2001,35(5):413-432.
[5] Lim A,Rodrigues B,Zhu Y.Airport gate scheduling with time windows[J].Artificial Intelligence Review,2005,24(2):5-24.
[6] Liu Qing.Wu Tongshui,Song Xianbo.Optimization of airport taxing planning during congested hours based on inmune clonal selectin algorithm[J].Transactions of Nanjing Universsity of Aeronautics & Astronautics,2012,29(3):296-301.
[7] Luo Rongwu,Xie Ruhe,Zhang Dezhi.Vertex coloring model and algorithm of gate assignment[J].Systems Engineering—Theory & Practice,2007,27(11):148-152.
[8] Chang Gang.Research on aircraft stands assignment and optimization in civil airport[D].Xi′an:Northwestern Polytechnical University,2006.(in Chinese)
[9] Zhu Shiqun.Research on gate reassignment problems in large airports[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.(in Chinese)
[10]Gu Y,Chung A.Genetic algorithm approach to aircraft gate reassignment problem [J].Journal of Transportation Engineering,1999,125(1):384-390.
[11]Yan Shang-yao,Tang Chung-hui.A heuristic approach for airport gate assignments for stochastic flight delays[J].European Journal of Operational Research,2007,180(3):547-567.
[12]Chang Gang,Wei Shengmin.Research on optimization of aircraft stands assignment problem[J].Journal of Civil Aviation University of China,2006,24(2):25-29.(in Chinese)
[13]Ulrich D,Andreas D,Yury N,et al.Flight gate scheduling:State-of-art and recent developments[J].The International Journal of Management Science,2007,35(3):326-334.
猜你喜欢
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- CALCULATION FOR KERNEL OF INTERVAL GREY NUMBER BASED ON BARYCENTER APPROACH
- FLEXURAL CAPACITY OF RC BEAM STRENGTHENED WITH PRESTRESSED C/AFRP SHEETS
- ACTIVE VIBRATION CONTROL OF TWO-BEAM STRUCTURES
- OUTPUT MAXIMIZATION CONTROL FOR VSCF WIND ENERGY CONVERSION SYSTEM USING EXTREMUM CONTROL STRATEGY
- MINIMUM ATTRIBUTE CO-REDUCTION ALGORITHM BASED ON MULTILEVEL EVOLUTIONARY TREE WITH SELF-ADAPTIVE SUBPOPULATIONS
- IMPROVED DOPPLER WARPING METHOD FOR AIRBORNE RADAR WITH NON-SIDELOOKING ARRAY
