Superconductivity in octagraphene

Jun Li(李军) and Dao-Xin Yao(姚道新)

1State Key Laboratory of Optoelectronic Materials and Technologies,School of Physics,Sun Yat-Sen University,Guangzhou 510275,China

2Key Laboratory for Microstructural Material Physics of Hebei Province,School of Science,Yanshan University,Qinhuangdao 066004,China

Keywords: octagraphene,s±superconductivity,square-octagon lattice,Fermi surface nesting

1. Introduction

As the chemical basis of the earth’s biology, carbon widely exists in most substances of life. Fullerenes, carbon nanotubes, graphene, every breakthrough on carbon has been widely concerned by the scientific community. So,could they surprise superconductivity research? Graphene, as the first two-dimensional (2D) material, has attracted much attention in the field of superconductivity.[1-5]However,the hexagonal structure and electronic band properties of graphene make it difficult to produce superconductivity,or introduce low superconducting transition temperature(Tc).[5,6]In 2018,Caoet al.discovered superconductivity in magic-angle twisted bilayergraphene.[7-10]However,due to the greatly reduced Fermi energy(～10 meV),its extremely lowTclimits its practical application. In addition to graphene, there are other isomers of carbon.[11]For example, although various forms of graphyne have been realized in experiments[12]which have the same hexagon symmetry with graphene, the superconductivity of graphyne has hardly come true.[13,14]

Recently, researchers found that octagraphene, a singleatom-thick allotrope of carbon composed of equal numbers of squares C4and octagons C8, may have the natural p-orbital high-temperature superconductivity.[15,16]Fermi surfaces of octagraphene have hole pockets and electron pockets in the case of half-filled electrons to form perfect nesting, which is conducive to the formation of high-temperature p-orbital superconductivity based on spin fluctuation.[15]The theoretical calculations show that the superconducting energy gap of octagraphene (～50 meV) is similar to that of d-orbital cuprate superconductors.[17]Moreover, the Fermi velocity of octagraphene(～106m/s)[18]is much higher than that of d-orbital iron-based superconductors.[19,20]Therefore, the coherence length in octagraphene should be much longer than that in cuprate and iron-based superconductors,which is conducive to the realization of superconducting quantum computation.[21]

Fig. 1. (a) Sketch of the square-octagon lattice and illustration of the intrasquare nearest-neighbor hopping t1 and the intersquare nearest-neighbor hopping t2. The dotted square denotes the unit cell. (b) Band structure of the TB model(Eq.(1))along the high symmetry lines in the first Brillouin zone. Panels (c) and (d) show the FSs of the undoped and 10% electrondoped cases,respectively. The site contributions on the FS sheets are shown by color: the red(green)represents that the weights contributed by the sublattices 1 and 3 (2 and 4) are dominant. The TB parameters are t1 =1,t2=1.2. Adapted from Kang et al.[15]

For the synthesis of 2D octagraphene group materials,different routes have been designed in theory,[22,23]and onedimensional carbon nanoribbons with squares C4and octagons C8rings have been synthesized experimentally.[24]On this basis,the actual preparation of octagraphene can be expected.

In this paper, we present an overview and prospect on octagraphene. Emphasis will be given to the related correlated electron theory and numerical simulations carried out by our group during the past years. The outline of the paper is as follows. In Section 2, several different studies on carbon octagons and squares rings of octagraphene by means of the first-principles calculations are presented. TheC4vsymmetry with versatile structurally favorable periodic sp2bonds is optimized using density functional perturbation theory(DFT).Section 3 is devoted to the theoretical model of the octagraphenes, including tight binding (TB) approximation and Hubbard model. Using the random-phase approximation(RPA), variation Monte Carlo (VMC) calculation and slaveboson mean field (SBMF) in Section 4, all three approaches consistently identify the single s±-wave pairing as the leading pairing symmetry. Fabricating suggestions are given in some possible routes to synthesize octagraphene, and some recent progresses have been reported for the related 2D materials in a controllable manner in Section 5.

2. First-principles calculations

Octagraphene has been studied by several research groups and thus has different names. In 1994, Zhuet al.called octagraphene as imaginary “4:8 carbon plane net”[25]during the study of the conjugated-circuit computations on 2D carbon networks. Then in 2011, the family of 12 alternative 2D flat carbon networks was studied by Enyashinet al., and octagraphene was examined as“network 7”.[11]In 2012, Liuet al.found that octagraphene has Dirac-like fermions and a high Fermi velocity similar to graphene based on the first-principles calculations, and they called it “planer T-graphene”.[18]Almost at the same time, inspired by the observations of line defects with octagons and pentagons,Shenget al.proposed a stable 2D periodic atomic sheet consisting of carbon octagons,coined it as “octagraphene”.[22]While studying a 84 set of Archimedean lattices in 2019,Crasto de Limaet al.reviewed the topological phases of octagraphene, named it “(4, 82)structure”, and observed aZ2=0 phase.[26]We here choose the name “octagraphene” with considering the octagons C8rings feature.

2.1. Geometrical structures

In general, as the first step, full geometry optimization was carried out for octagraphene. The lattice constant of the square cell is arounda0=3.47 ˚A,3.45 ˚A,3.42 ˚A,3.446 ˚A and 3.444 ˚A, depending on different DFT methods.[11,16,22,23,26]Similar to graphene, every carbon atom in octagraphene has three sp2-bonded nearest neighbors, forming threeσ-bonds.In addition, octagraphene has two types of bond lengths,1.48 ˚A (intra-squares) and 1.35 ˚A (inter-squares), and the bonds of each carbon atom have angles of one 90°and two 135°.[22]The relative positions of carbon atoms in a cell are almost independent of the lattice constant.[16]As shown in Fig. 2(b), the positions of four carbon atoms in a cell are(0.50a, 0.20a), (0.20a, 0.50a), (0.50a, 0.80a) and (0.80a,0.50a) respectively, and consistent withC4vsymmetry, 2D space groupp4mor#11(p4mm).

Fig.2. Left: the predicted structure of octagraphene from DFT calculation.The relative positions between the layers form the A-A stacking. Right:structure of single-layer octagraphene. The relative positions of four carbon atoms in a unit cell are independent of the deformation. Adapted from Li et al.[16]

Besides, the situations of multi-layer octagraphene and bulk octagraphene (octagraphite) have also been studied.[16]Due to theC4vsymmetry of single-layer, there are three possibilities for stacking two octagraphene layers: A-A stacking,A-B stacking and A-C stacking. We find that the A-A stacking is the most stable compared to the other two. Otherwise from A-A stacking to A-B and A-C stacking, the energy gap is rarely small comparing with that for graphene. This indicates a weaker inter-layer coupling,making the material more slippery than graphite.[27]In other words,this reflects the 2D nature of octagraphite.

2.2. Band structures

The band structure shows that undoped octagraphene is metallic,[11,18]as shown in Fig. 3. More electrons are distributed on the inter-square bonds C4than on the intra-square bonds C8in octagraphene,showing an unequal sp2hybridization character. The top of valence band and the bottom of conduction band are located at theΓandMpoints in the Brillouin zone, respectively. There is an indirect negative band gap about 4.03 eV,[22]leading to the Fermi level passing through both the conduction and valence bands. The band structures contain a hole pocket around theΓpoint and an electron pocket around theMpoint, which is similar to those of cuprates,[17]iron-based superconductors,[20]and new found Ni-based superconductors.[28]TheΓandMpoints haveC4vsymmetry,and theXpoint hasC2vsymmetry,resulting in the doubly degenerate band structure on theΓandMpoints. In the ideal case,the two pockets connected by the perfect nesting vectorQ=(π,π)form the perfect Fermi-surface nesting.On the other words, the hole and electron pockets share the same area.[16]

Fig.3. Left: Electronic band structures and density of states(DOS)of octagraphene calculated by DFT and TB approximation.Adapted from Sheng et al.[22]Right:Fermi surface of octagraphene,where the hole packet(yellow)is at the Γ point,and the electron pocket(green)is at the M point.The Fermi surface is well nested by the vector Q1=(π,π).

The projected DOS of octagraphene shows that the energy bands near the Fermi surface are predominantly contributed by the 2pzorbital of carbon atom. It is mostly dominated by theπbands, which is the same as that in graphene.[18,23]By neglecting the second and higher order terms, the Fermi velocity of octagraphene is estimated to be about～106m/s according tovF≃E(q)/|q|,[23]which is close to the theoretical value of graphene[29]and higher than that of d-orbital iron-based superconductors.[19,20]

In Fig.4, for larger lattice constanta, the electron orbits are more localized and have less overlap. The smaller lattice constantaleads to precipitous band structures and makes energy bands overlap with others. The nearly perfect Fermisurface nesting is independent of the stress or strain along the layer.[16]The ultimate strain of octagraphene is about 1.3a0to 1.4a0.[22]Fora/a0=0.9 in Fig. 4(c), the bands are quadruplely degenerate at theMpoint withE=-3.01 eV.[16]This coincidence is different from the Dirac point. The structure is not a bi-conical structure with linear dispersion, but a parabolic dispersion. It means that the low-energy excitations are no-longer massless.

Fig. 4. Band structures of different lattice constant a: a/a0 =1.1, 1.0 and 0.9[a0=3.44 ˚A].DFT calculated results,solid lines;fitting results obtained by TB model,dashed lines. For a/a0=0.9,the bands show a quadruple degeneracy at the M point with E=-3.01 eV.From Li et al.[16]

For multi-layer octagraphene, each band of single-layer splits into multi bands due to the multiplied unit cell. As a result,there are several nesting hole pockets around theΓpoint and several nesting electron pockets around theMpoint. For octagraphite,as shown in Fig.5(a),the DFT calculated structure within a layer is almost the same as that of single-layer octagraphene, only slightly larger in size. There are always four bands near the Fermi level for a givenkz, which shows the 2D feature of octagraphene materials. The highest and the lowest boundaries of each band are marked bykz=0 andkz=π, respectively. The 3D Fermi surface has a fusiform,where the largest hole pocket is around theΓpoint. It also has similar spindle shape as those in cuprates,[17,30]iron-based superconductors,[20,31]and new found Ni-based superconductor family.[28]

Fig. 5. (a) Band structures of the bi-layer octagraphene with a0 =3.45 ˚A.The solid lines represent the results by DFT calculation. The dashed lines are fitting results of TB model. (b)Fermi surface of bi-layer octagraphene.The nesting vectors Q2 =(π,π), (π+δ,π+δ) and (π-δ,π-δ) mean the deviation of perfect Fermi surface nesting. (c)Band structures of octagraphite with kz=0,π/2,π. (d)Fermi surface of octagraphite,the nesting vector is almost Q∞=(π,π,π). Adapted from Li et al.[16]

2.3. Mechanical stability

According to the previous works,[18,22,23,26,32]no imaginary phonon modes are found in phonon spectra of octagraphene, implying that octagraphene is kinetically stable.The calculated total energy per atom of the octagraphene is 0.53,0.52,0.513,0.50,0.707 eV above graphene,depends on the different methods,[11,18,22,26,33]which is lower than the Tcarbon(～1.31 eV),[34,35]graphdiyne(～0.77 eV),[36,37]graphyne (～0.66 eV)[38,39]and graphane (～2.99 eV),[40,41]all of which have already been experimentally obtained,suggesting that octagraphene is metastable against graphene. Molecular dynamics simulations also indicate that octagraphene can hold stability even at a high temperature.[18,22,42-44]

The mechanical properties of octagraphene are also similar to those of graphene according to previous reports.[22,33,45,46]As it has aC4vsymmetry,two independent elastic constants are 296 N/m and 46 N/m, respectively. The Young’s modulusEof octagraphene is obtained to be 306 N/m and 168 N/m along the two directions,respectively,in comparison to those of graphene (350 N/m).[47]The ultimate tensile strength or the breaking strength of octagraphene is 34.4 N/m and 27.3 N/m along the two directions,respectively,which are quite comparable with those of graphene (38.4 N/m, zigzag direction and 34.8 N/m,armchair direction).[47]The Poisson’s ratios of octagraphene are 0.13 and 0.47 along the two directions, which are comparable with 0.21 (zigzag direction) and 0.17 (armchair direction) of graphene.[48]Octagraphene has the mechanical properties very similar to graphene and might be the strongest carbon atomic sheet after graphene till now.

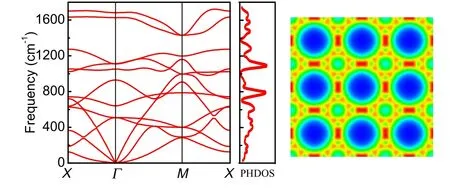
Fig. 6. Phonon dispersion and orbital projected band structure of octagraphene. Adapted from Lima et al.[26]

3. Models

3.1. TB model

As octagraphene has two types of bond lengths, the TB Hamiltonian for electrons in octagraphene has the form[16]

Fig.7.The 2D single-orbital TB model.Left:square-octagon lattice.Right:1/5 depleted square lattice. They are topologically equal. The t1,t2 and t3 correspond to the intra-square,inter-square and diagonal hopping energies,respectively.

There are four bands∊1,∊2,∊3and∊4by diagonalizing the matrix Eq. (2). Based on the fittings,[16]the parameters should bet1=2.678±0.033 eV,t2=2.9801±0.027 eV andt3=0.548±0.024 eV whena/a0=1.0. Also some other fittings givet1=2.5 eV andt2=2.9 eV.[22]In comparison,t ≈2.7 eV of the nearest-neighbor hopping energy andt′≈0.1 eV of the next nearest-neighbor hopping energy were reported in graphene.[29,50-52]

Thet3is much smaller thant1andt2because the distance between the atoms along diagonal directions on squares is much longer than that of the nearest neighbors. As a result,t3is missing in the earlier studies.[15,22,26]Note that this smallt3is necessary to split the∊3and∊4at theMpoint, and thus makes∊2to coincide with∊3here. In other words,ift3=0,∊3and∊4overlap at theMpoint.

The values oft1,t2decrease with the increase ofa, butt2/t1almost remains 1.1 when theachanges from 0.90a0to 1.20a0. The pzorbitals have an azimuthal symmetry, and therefore their interaction with neighbor pzwill be only distance dependent,[26]thust1/t2is independent ofaand the Fermi surface stays unchanged. On the other hand, the TB model Eq. (1) is credible because of the well fits of the DFT calculated bands.[16]

For bulk octagraphite, the matrix form of the 3D TB model is written as

in whicht1=2.686±0.017 eV,t2=2.986±0.013 eV,t3=0.574±0.012 eV andt⊥=0.259±0.005 eV from Liet al.’s fitting.[16]Allthere have little difference from those in singlelayer octagraphene. Notice thatt⊥here is much smaller than that of graphene(t⊥≈0.4 eV).[51]

Interestingly,in addition to the four energy bands near the Fermi level,other bands are almost the same and independent of the number of layers from the DFT results. These energy bands have almost no contribution to the interaction between layers, they are reflected by the local properties of orbit and have little influence for superconductivity.

Table 1. The lattice constant a0,fitting parameters t1,t2,t3,t⊥and λ of one to six layers of octagraphene and bulk octagraphite(∞).

3.2. Hubbard model

Similar to graphene, there are Coulomb interactions between the 2pzelectrons in the octagraphene materials.[51,53,54]This local part of Coulomb interaction is also crucial for the theory of defect-induced magnetism in graphene.[55,56]The effective Hubbard model is used to describe the effects

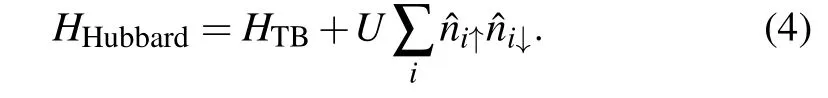
Here theU-term represents the effective on-site Coulomb interaction between the 2pzelectrons. There were some references in evaluatingUin carbon-based materials, such as 16.9 eV in benzene,[53]10 eV in polyacetylene[57,58]and 9.8 eV in graphene.[59]

This kind of octagraphene-like square-octagon lattice has been studied from different perspectives. The quantum phase transitions in square-octagon lattice were investigated by Kargarianet al.,[60]Baoet al.,[49,61]Silet al.,[62]Limet al.[26]and Pomataet al.[63]There are also applications in mathematical and theoretical computer science,such as packed loop models[64]and Markov chain.[65]

The square-octagon lattice was found in some other materials, such as octagon-structure monolayer of nitrogen,[66-68](10¯10) surfaces of ZnO,[69]alkaline iron selenideA2Fe4Se5(A= K,Rb,Cs,Tl),[70]magnetic CaV4O9compound,[71]2D transition metal dichalcogenides[72]and single-layer GaN and AlN.[73]

4. Superconductivity

For Hubbard model shown in Eq.(4), three different approaches used to treat the model with different limits ofUgive almost the same pairing symmetry and antiferromagnetic order. For the weak-,strong-,and intermediate-coupling strengths,the suitable calculations consistently yield standard s±-wave superconductivity in this simple one-orbital system.

4.1. Weak-coupling limit

The standard multi-orbital RPA[74-86]approach was used to treat the weak-coupling limit of the model. The largest pairing eigenvalueλis used to estimateTcby the following equation:[79,87]

Eventually,λ= 0.321 fora/a0= 1 andTc～190 K are obtained for the single-layer octagraphene.[15,16]With decrease ofa,Tcdecreases in a limited scale.However,Tcwould remain at very high level (>100 K) whateverais. In other words, single-layer octagraphene would be a good superconductor with limited mechanical deformation based on RPA.[16]

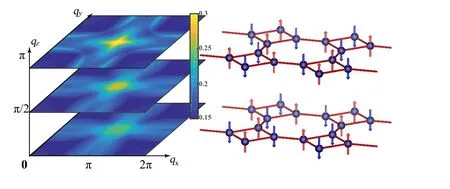
Fig. 8. Superconducting properties of octagraphite. Left: the eigensusceptibilities χ(q) with qz = 0, π/2, π. χ(q) peaks at almost Q∞=(π,π,π). Right: Predicted antiferromagnetic N´eel pattern with half-filling.Adapted from Li et al.[16]

TheTc～170 K is obtained for three to five layers and satuates at about 160 K for six layers and more, suggesting that superconductivity is mainly determined by the 2D characteristics of the material.[16]This phenomenon is similar to 2D high-temperature superconductivity, such as monolayer Bi2Sr2CaCu2O8+δ.[89,90]

4.2. Intermediate-coupling

The RPA approach shows that superconductivity in octagraphene is unconventional and mediated by the antiferromagnetic spin fluctuations. However,as the effective superexchange parameterJfor real materials with intermediateUis hard to study,Tcobtained here might not be accurate. In the following, the VMC approach was considered to study the problem[15,91]

Hereg ∈(0,1)is the penalty factor of the double occupancy,Neis the total number of electrons,and[92,93]

whereΔαk=Δα f(k) is the superconducting gap function.Here only intra-band pairings on theα=2,3 bands crossing the Fermi surface are considered.

Theδdependence of the energy per unit cell for each form factor is shown in Fig.5(a)forU=4t1=10 eV for a typical dopingx=10%,withgandµcoptimized for eachδ.Note that the optimizedg=0.5475 is almost equal to the optimized value without SC,and thatµcis almost equal to the value obtained in the mean-field calculation. From Fig.9(a),one finds that the s±-wave pairing causes the most energy gain among the four gap form factors, with the optimized gap amplitude atδ=0.022t1≃50 meV,comparable with cuprates,implying similarTcbetween them. The gap function of the s±-wave SC obtained is shown on the Fermi surface in Fig.9(b),which is well consistent with that obtained in the RPA calculation.[15]

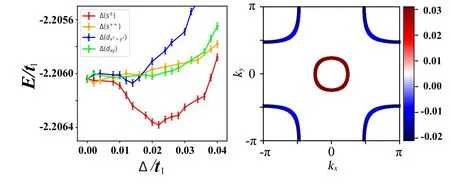
Fig.9. The VMC results. Left: energy per unit cell as function of δ for the four different gaps. Right: the s±-wave gap function projected on the Fermi surface. Adapted from Kang et al.[15]

4.3. Strong-coupling limit

In the strong-coupling limit,the Hubbard model becomes an effectivet-Jmodel[86]

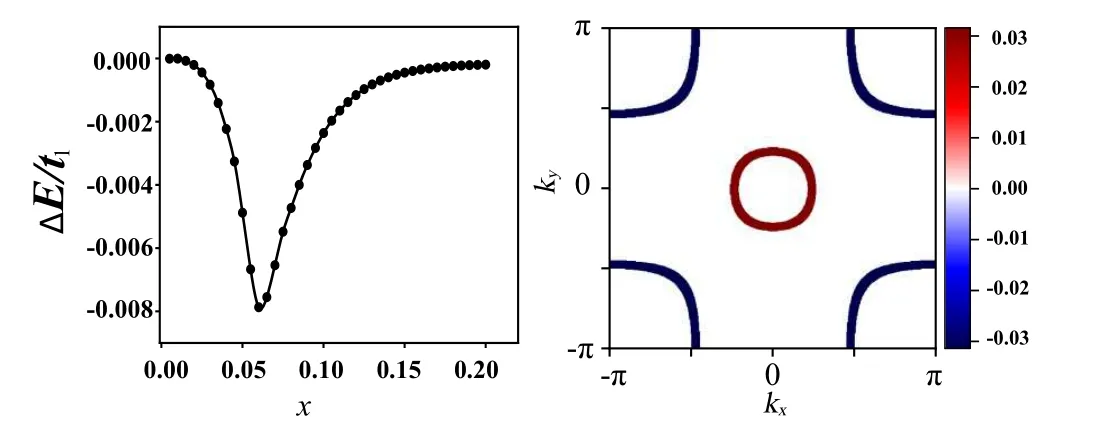
Fig. 10. The SBMF results. Left: doping dependence of the energy (per unit cell) difference between the s±-wave pairing and the d-wave one,ΔE =Es-Ed, in units of t1. Right: the s±-wave gap function projected on the Fermi surface. Adapted from Kang et al.[15]

4.4. More discussion

The Heisenberg Hamiltonian Eq. (8) for square-octagon lattice (or 1/5-depleted square lattice) has been widely studied since the realization of CaV4O9.[71,102-107]Magnetic phase diagram and Mott transition were found with frustrations.[108-114]Then this magnetic structure was also realized in alkaline iron selenideA2Fe4Se5(A=K,Rb,Cs,Tl)single crystals.[70,115]

In 2019, Guet al.investigated superconducting properties of octagraphene based on electron-phonon coupling and Allen-Dynes modified McMillian equation.[116]From BCS theory, they obtainedTcup to around 20.8 K at ambient pressure.[23,117]In 2020, Nuneset al.found flat-band superconductivity[118]for tight-binding electrons on squareoctagon lattice. Similar to twisted bilayer graphene, they suggested thatTcmight reach a high value.[119]Interestingly,when consider the similar 1/5-depleted square lattice Hubbard Model at half-filling,the dominant pairing symmetry changes character from d wave in the plaquette phase to an extended s wave in the N´eel phase,[88]revealing a good agreement with octagraphene.

We notice that the bi-layer octagraphene can enter the superconducting state by applying a vertical electric field between the layers even without doping.[120]This will greatly facilitate the manipulation of superconductivity. All these studies have come to the same conclusion: octagraphene could be a good platform for high-Tcsuperconductivity.

5. Experimental realization

5.1. Synthetic progress

So far there are already some octagraphene related materials reported. Similar to carbon nanoribbons, octagraphene nanoribbons rolled from octagraphene were predicted to be mechanically stable and promising for the development of electromagnetic radiation sensors.[22,121-123]When the C4of the octagraphene layers are bonded to each other, the bulk Tgraphene similar to octagraphite was predicted to have a high Fermi velocity.[18,124,125]The 2D Dirac material S-graphyne was found to contain two sizes of squares C4rings,[126]similar to both graphyne and octagraphene. Moreover, squareoctagon pair(4|8)was also discovered in 2D boron nitride(h-BN).[127-129]

Finally, let us look back to the progress in octagraphene experimental synthesis. The separate square C4rings[130,131]and octagon C8rings[131]were realized long ago chemically.The C8-C5sp2-hybridized carbon rings were realized by onedimensional topological defects in graphene.[132-134]The C4-C6cyclic dehydrogenative C-C coupling was obtained using on-surface synthesis.[135,136]Graphene-like nanoribbons periodically embedded with C4-C8structures were fabricated successfully on Au(111).[24]

In 2021, Fanet al.synthesized an ultraflat biphenylene carbon sheet consisting of sp2-hybridized carbon atoms forming C4, C6and C8on a gold surface.[137]The 2D biphenylene sheet presents a metallic character, and also in the planar strips with zigzag-type edges. Armchair-edged strips develop a band gap that decreases monotonically with the ribbon width.[138-140]We have found that this material has a C4-C8structure in just one direction and the remaining C6structure may be harmful to the superconductivity.[120]

5.2. Fabricating routes

Octagraphene has similar mechanical properties as graphene[47]and might be the strongest carbon atomic sheet after graphene till now according to previous reports.[22,33,45]However, directly rotating C-C bonds from graphene lattice to octagraphene has a huge energy barrier (up to 7 eV).[141]Moreover, these processes from honeycomb and squareoctagon lattices were examined to be quite hard by kinetic Monte Carlo simulations.[142]

There were four theoretical synthetic routes reported for octagraphene.[22,23,47,143]One route is to make the line defects periodically in graphene and then connect properly the broken bonds of carbon atoms.[22]The second route is to use large uniaxial stress beyond the fracture limit[47]to convert graphene to two periodic pentaheptite structures, then further into octagraphene. The third route suggests to exfoliate the bulk C4K,C4Li or C4Na with similar electrochemical method used in graphite intercalation compounds.[1,23,144,145]The last one proposes an atom-mimicking design concept to achieve direct self-assembly of 2D low-coordinated open lattices to compose octagraphene.[143]Other synthetic routes to realize octagraphene are possible.

6. Conclusions

In summary, an overview on the progress of superconductivity in the octagraphene has been presented. The geometrical and band structures of octagraphene show more 2D characteristic than that of graphene and can hold mechanical stability even at high temperature. Octagraphene is believed to be an ideal system to study superconductivity. The perfect Fermi surface nesting from undoped octagraphene can induce the long-ranged SDW order. Upon doping or applying a vertical electrical field on the multi-layer octagraphene, highTcsuperconductivity is expected. The RPA, VMC, and SBMF approaches for the weak-, intermediate-, and strong-coupling strengths consistently yield the standard s±-wave superconductivity,respectively. Besides,octagraphene may have traditional p-orbital superconductivity with considerableTcbased on the electron-phonon coupling calculations. These mechanisms may coexist in octagraphene for realizing the possible highTcsuperconductivity. So far, there were already experiments which can realize 2D carbon materials with square C4rings and octagon C8rings structures.For example,an ultraflat biphenylene carbon sheet consisting of C4-C6-C8was synthesized recently. Theoretically,at leat four synthetic routes were reported for octagraphene,and new surface synthesis route is on the way. Furthermore, octagraphene is supposed to have long superconducting coherence time based on its 2D nature and large Fermi velocity from p-orbitals, which is conducive to quantum computation.

Acknowledgments

This project is supported by the National Key R&D Program of China (Grant Nos. 2017YFA0206203 and 2018YFA0306001), the National Natural Science Foundation of China (Grant No. 11974432), GBABRF-2019A1515011337, Natural Science Foundation of Hebei Province, China (Grant No. A2021203010), Shenzhen Institute for Quantum Science and Engineering (Grant No. SIQSE202102), and Leading Talent Program of Guangdong Special Projects.