地面微地震资料弱信号提取方法研究

宋维琪，杨勤勇，郭全仕，姜宇东，何 柯

（1.中国石油大学（华东）地球科学与技术学院，山东青岛266580；2.中国石油化工股份有限公司石油物探技术研究院，江苏南京211103）

地面微地震记录有效信号在时间采样方向具有局部脉冲的特点。根据频带宽度的不同所呈现的地震波形可以是单相位波形也可以是多相位波形［1－3］，并且地震波振幅在其初跳响应达到最大值之后迅速衰减；在空间方向随离开震源方向其振幅逐渐衰减。地面微地震实际记录的信号是有效信号和各种噪声的叠加结果，信号分离的难易程度由信噪比决定，大部分地面微地震信号的信噪比较低，特别是当有效信号较弱时，被完全淹没在噪声中。目前，讨论研究的弱信号监测问题［4－6］大都是针对具有周期或准周期重复性的有效信号的监测进行的，而对于微地震信号，在时间方向类似随机脉冲的弱信号的监测问题就变得更加困难。

有效信号提取和噪声压制都是根据有效信号和噪声的差异特征［7－9］设计不同方法进行处理的，如：随机噪声压制是根据其自身的白谱特点通过谱的差异设计相应的方法进行去噪处理，去除局部强干扰是根据能量突变的特点设计相应方法进行处理，去除相关噪声尤其是水平相关噪声是根据视速度特点，等等。地面微地震资料有效信号提取的难点是如何去除各种类型的相关噪声，如机器噪声、人工干扰、浅层各种散射波等［10］。国内外多位学者［11－13］利用多固定源建模方法剔除这些相关噪声，取得了一定的成果，但是应用效果尚不理想。实践证明，这些多个固定源产生的噪声大都具有局部随机变化的特点，因此很难建立某种固定的噪声模型，当多个固定源产生的相关噪声相互干涉叠加后，产生了一种更加复杂的类似随机噪声的相关噪声。另外，地面微地震信号由于传播距离远，到达地面后有效信号十分微弱。因此，针对这些特点，研究了地面微地震资料的弱有效信号提取方法。

1 时空方向高阶统计量计算方法

若x1，x2，x3，x4为零均值的随机变量［14－15］，其四阶累积量为

式中：E（x1，x2，x3，x4）表示4个变量的数学期望值；E（xi，xj）表示2个变量的数学期望值。

具体计算公式是

式中：Δt为时间采样间隔；k1＝1，2，…，M1；k2＝1，2，…，N1；k3＝1，2，…，L1。

高阶累积量对非相关噪声和高斯噪声具有有效的抑制作用。这种被抑制噪声的特点必须是统计意义下其数学期望值是零，即对取定某个大小样本空间内（窗口大小），其噪声的期望值是零。进一步说，如果某类信号在给定样本空间内，其期望值是常数，则通过高阶累积量计算，也能够进行有效抑制。从地面微地震有效信号的时空分布特点了解到，在时间方向，有效信号呈现出衰减脉冲且一般不具有对称性的特点，并且在时间序列记录的某个局部时间范围内微地震有效信号是一小段局部时间脉冲。在这一小段时间范围窗口内，其数学期望值不是常数，如果在这个窗口内，其它信号的数学期望值是常数，则其它信号就得到了抑制。因此，利用高阶累积量在时间方向监测微地震脉冲信号具备了一定的分离条件。当然，这个条件由微地震有效信号的特点所决定。

一般情况下，干扰信号在较小时间窗口（样本空间）其均值不是常数，且随着窗口的不同而不同，即在时间方向通过高阶累积量的计算不可能完全消除干扰。对于多道地面微地震记录资料，记录的有效信号的振幅是缓慢变化的，在横向局部范围内即横向窗口较小时，近似认为相等；但在横向窗口较大时，不同窗口的数学期望值（均值）不等。假定有效信号在横向分布范围较大且振幅变化的条件下（这个条件其实是自然满足的），可以利用高阶累积量在横向方向进行有效信号的提取计算。

式中：Δx为道间距；k1＝1，2，…，M2；k2＝1，2，…，N2；k3＝1，2，…，L2。

综合两个方向的结果得到

随着社会经济水平的高速发展，企业自身的发展需要紧跟时代发展的步伐。传统财务会计的存在，已经无法满足数据时代的要求。因此，财务会计向管理会计的转型是十分有必要的。对于企业设置管理会计的优势主要表现在两个方面：一方面，管理型会计能够具备财务会计最基本的会计技能，方便处理财务数据；另一方面，管理型会计能够具有一定的企业管理能力，可以实现相应的管理，另外管理型会计的存在还能够对数据进行预测分析，能够避免投资风险，降低企业运行的成本［1］。

式中：λ1，λ2为加权系数。

2 基于贝叶斯框架的四阶累积量的自适应算法

对于振荡较严重的信号，利用贝叶斯估计方法比用最小二乘估计方法稳定［16－18］。贝叶斯估计一般采用后验概率最大方法。

对参数的最优估计问题，等价为在贝叶斯理论下，具有先验信息条件时，经过贝叶斯推理，得到目标函数的极大后验概率。对于弱信号提取估计问题，假设信号s受到噪声n污染，则

式中：y是含噪声的信号；n是均值为0，方差为σ2的高斯白噪声。如果事先知道s的统计特性，则根据贝叶斯估计可以由含噪声的信号y对真实信号s做出估计

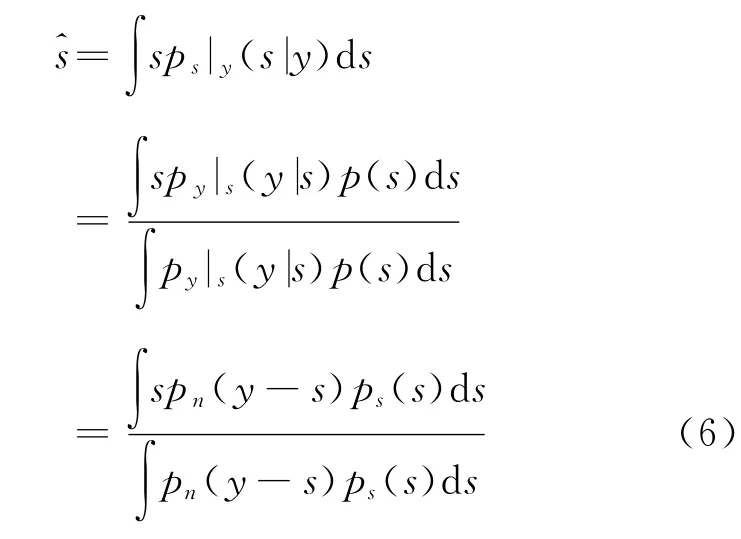
式中：pn为噪声的概率密度函数；ps为有效信号的先验概率密度函数；py为记录信号的概率密度函数。

如何得到最大后验概率是贝叶斯估计的关键问题。后验概率密度是通过先验概率密度和样本计算获得的。先验概率分布或先验概率密度函数可以由参考信号得到，也可以从样本中得到。我们从样本的高阶累积量中计算先验概率密度。

设 N 维高阶累积量X＝［x1，x2，…，xn］，其均值为a＝［a1，a2，…，an］。协方差矩阵为

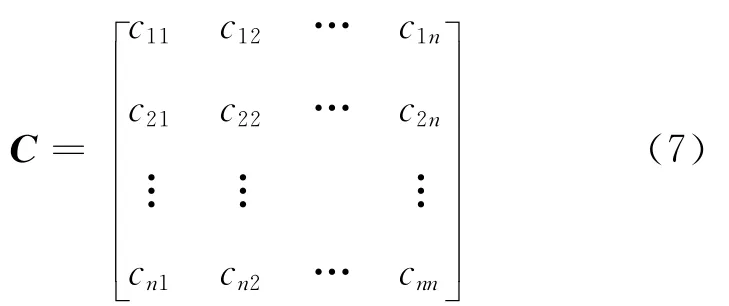
N维高阶累积量X的联合概率密度函数为

在给定样本空间下，后验概率是概率密度函数和分布函数的积分值。如果数据出现奇异，则积分结果奇异。因此，为了获得稳定的后验概率值，需要从计算结果利用回归方法或拟合方法，得到理论模拟概率密度函数，然后再计算后验概率。

为了提取有效信号，最大程度地压制噪声，我们通过先验概率和后验概率的不断更新，实现最大后验概率估计。

当p（s｜y）容易计算时，解方程

一般情况下，由于

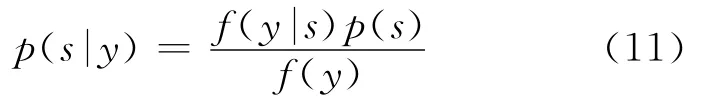
f（y｜s）p（s）与p（s｜y）最大值等价，可解方程

来求最大后验估计量。式中：f（y｜s）为信号的条件概率密度。

上述方程是有效信号的条件概率和有效信号的先验概率组成的求极值方程，该式的等价形式为

3 自适应减法

上述方法较好地压制了邻域噪声，相对提高了弱信号的强度［19－20］，但还有一些区域性分布的相关噪声没有完全去掉，并且这些区域性的相关噪声和弱有效信号在一个数量水平上。这些区域性噪声相对有效信号来说，几乎均匀分布。结合地面微地震有效信号在时间上是局部邻域分布的特点，区域相关噪声可以通过以当前采样点为中心窗口内的各采样点值减去离开窗口较远多个窗口平均采样点值的方法进行剔除，计算表达式为

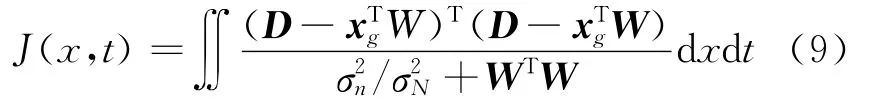
式中：D为当前采样点为中心的窗口内的采样点数据；W为算法中使目标函数最小的权函数；xg为离开当前采样点较远采样点数据；σn为当前样点数据噪声方差；σN为较远样点数据噪声方差。算法中窗口大小通过自动调节的办法进行选取。

4 处理效果分析

我们利用的资料是经过预处理后的实际地面微地震资料。预处理包括直流分量、强噪声、50Hz工业干扰噪声、强能量相关噪声等的剔除处理。在此基础上进行有效信号提取处理。图1和图2分别为第5条和第7条测线的处理结果。对比分析各种方法的结果可以看出，预处理结果在前40道能够隐约地看到有效信号，40道以后几乎看不到有效信号（图1a，图2a）。经累积量计算处理后，40道以前的有效信号清楚，40道至80道的有效信号也得到揭示，只是连续性不好（图1b，图2b，图1c，图2c）；经自适应减法处理后效果得到明显改善（图1d，图2d）。

图1 实际地面微地震资料第5条测线各研究方法处理结果

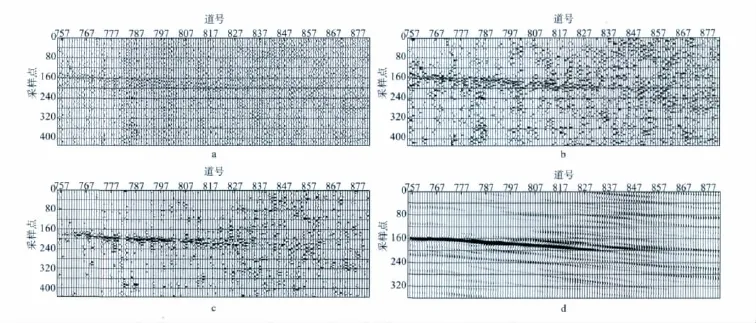
图2 实际地面微地震资料第7条测线各研究方法处理结果

5 结束语

地面微地震有效信号的时空分布呈现出衰减脉冲的特点，并且出现在时间序列记录的某个局部时间范围内，是一小段局部时间脉冲。干扰信号和有效信号的统计特征随着样本空间大小的变化而变化。对于实际的地面微地震资料的弱信号提取处理来说，样本空间大小选取直接关系到有效信号提取的置信程度。利用信号四阶累积量的联合概率密度函数比直接利用原信号概率密度函数进行后验估计的效果更好。提取弱信号的同时不可避免地会提取弱的无用相关信号，使得弱有效信号不易识别。利用自适应减法剔除这种区域相关噪声，取得了一定成效。通过系列方法的合理分析研究和实际资料处理，较好地实现了地需监测微地震资料弱有效信号的分离提取。

［1］Liu X C，Liu X L.Weak signal detection research based on duffing oscillator used for downhole communication［J］.Journal of Computers，2011，6（2）：359－367

［2］Refae A B，Khalil S，Vincent B，et al.Increasing bandwidth with single sensor seismic data—the Lehib oilfield case study［J］.First Break，2008，26（1）：79－84

［3］Strobbia C，Glushchenko A，Laake A，et al.Arctic near surface challenges：the point receiver solution to coherent noise and statics［J］.First Break，2009，27（1）：69－76

［4］Mancini F，Fairhead S，King A，et al.Data quality uplift from a dual－azimuth acquisition offshore Libya［J］.Expanded Abstracts of 80thAnnual Internat SEG Mtg，2010，17－22

［5］Mougenot D，Cherepovskiy1A，Liu J J.MEMS－based accelerometers：expectations and practical achievements［J］.First Break，2011，29（2）：85－90

［6］Kendall R，Jin S D，Ronen S.An SVD－polarization filter for ground roll attenuation on multicomponent data［J］.Expanded Abstracts of 75thAnnual Internat SEG Mtg，2005，928－932

［7］Franco R，Musacchio G.Polarization filter with singular value decomposition［J］.Geophysics，2001，66（3）：932－938

［8］梁军利，杨树元.一种基于非周期随机共振的微弱信号检测方法［J］.微计算机应用，2007，28（11）：1121－1126 Liang J L，Yang S Y.A method based on stochastic resonance weak signal detection method［J］.Micro Computer Application，2007，28（11）：1121－1126

［9］何大海，赵文礼，梅晓俊.基于随机共振原理的微弱信号检测与应用［J］.机电工程，2008，25（4）：71－74 He D H，Zhao W L，Mei X J.Based on the principle of stochastic resonance weak signal detection and its application［J］.Mechanical and Electrical Engineering，2008，25（4）：71－74

［10］辛春雨，刘凤侠，张宇.结合数字滤波技术的随机共振弱信号检测［J］.吉林大学学报（理学版），2009，47（2）：358－361 Xin C Y，Liu F X，Zhang Y.Combined with digital filter technology of stochastic resonance weak signal detection［J］.Journal of Jilin University（Natural Science Edition），2009，47（2）：358－361

［11］Harris D B，Jarpe S P，Harben P E.Seismic noise cancellation in a geothermal field［J］.Geophysics，1991，56（10）：1677－1680

［12］Candy J，Followill F.Multichannel noisecancellation：a seismic application［J］.Mechanical Systems and Signal Processing，1989，3（3）：213－228

［13］Vincent P D，Tsoflias G P，Steeples D W，et al.Fixed－source and fixed－receiver walkaway seismic noise tests：a field comparison［J］.Geophysics，2006，71（6）：W41－W44

［14］杨宇山，李媛媛，刘天佑.高阶统计量在地震弱信号及“磁亮点”识别中的应用［J］.石油地球物理勘探，2005，40（1）：103－107 Yang Y S，Li Y Y，Liu T Y.Higher order statistics in seismic signal and“magnetic bright spot”in the application of recognition［J］.Oil Geophysical Prospecting，2005，40（1）：103－107

［15］王晶，张庆，梁霖，等.采用遗传算法的自适应随机共振系统弱信号检测方法研究［J］.西安交通大学学报，2010，44（3）：32－36 Wang J，Zhang Q，Liang L，et al.The genetic algorithm of adaptive stochastic resonance weak signal detection method［J］.Journal of Xi’an Jiao Tong U－niversity，2010，44（3）：32－36

［16］高晋占.微弱信号检测［M］.北京：清华大学出版社，2004：1－36 Gao J Z.Weak signal detection［M］.Beijing：Tsinghua University Press，2004：1－36

［17］张鑫，井西利.一种基于正态反高斯模型的贝叶斯图像去噪方法［J］.光学学报，2010（1）：71－74 Zhang X，Jing X L.A method based on normal inverse Gauss model Bayesian image denoising method［J］.Journal of Optics，2010（1）：71－74

［18］詹海刚，施平，陈楚群.基于贝叶斯反演理论的海水固有光学特性准分析算法［J］.科学通报，2006，51（2）：204－210 Zhan H G，Shi P，Chen C Q.Based on Bayesian inversion theory of inherent optical properties of seawater analysis algorithm［J］.Chinese Science Bulletin，2006，51（2）：204－210

［19］吴逍，纪国宜.基于谐波小波包理论检测微弱信号的研究［J］.电子测量技术，2010，33（6）：1－3 Wu X，Ji G Y.Based on harmonic wavelet packet theory study of weak signal detection［J］.Electronic Measurement Technology，2010，33（6）：1－3

［20］李舜酩，许庆余.微弱振动信号的谐波小波频域提取［J］.西安交通大学学报，2004，38（1）：51－55 Li S M，Xu Q Y.Weak vibration signal extraction of harmonic wavelet in frequency domain［J］.Journal of Xi’an Jiao Tong University，2004，38（1）：51－55