地震波叠前逆时偏移脉冲响应研究与应用

陈可洋，吴清岭，范兴才，陈树民，李来林，关 昕，刘振宽

（1.中国石油天然气集团公司大庆油田有限责任公司勘探开发研究院，黑龙江大庆163712；2.中国石油天然气集团公司大庆油田有限责任公司勘探分公司，黑龙江大庆163453）

地震波叠前逆时成像技术是当前实现复杂构造地震波高精度成像方法中较为成熟且最精确的成像方法之一［1］。逆时偏移方法可在时间－空间域和频率－波数域实现，其具体计算过程包括地震波正演模拟和检波点波场的逆时延拓，并通过应用逆时成像条件（相关法成像条件等）来实现复杂构造地震波场的逆时成像。整个迭代过程只需保证数值计算过程稳定和精确的要求［2－5］。地震波逆时偏移在具体数值传播机理方面完全借用了地震波正演数值模拟相关数值理论和计算方法。由于逆时偏移方法采用双程地震波波动方程，不需要将逆时偏移方程进行上、下行波波场算子分离处理，且能够遍历整个计算模型区域，且方法本身对地震波动方程的近似较少，因此，它适合于任意陡倾角和速度在纵、横向变化较为剧烈情况的叠前偏移成像，从而可以弥补单程地震波动方程偏移方法受地层倾角限制的缺陷和解决克希霍夫叠前深度偏移方法的多值走时和计算盲区的问题［6－9］。与此同时，地震波逆时偏移方法还可以实现多次波、回转反射波等通常认为是干扰波类型波场的准确成像（而克希霍夫深度偏移方法和单程波偏移方法均将多次波等波场当作一次反射波进行处理，这必然产生较大的误差），且能够准确地处理焦散面的多值走时和相位变化问题，这正是当前地震波叠前逆时成像技术受到地球物理学界的充分重视并广泛应用的原因［10－11］。随着计算机技术的快速发展，特别是基于CPU／GPU高性能集群并行计算技术和大容量磁盘的快速存储技术的出现［12］，较大程度地改善了逆时偏移技术工业化应用的现状，同时也为地震波全波形反演方法的工业化应用奠定了基础。

目前关于如何实现高精度地震波叠前逆时成像的问题引起了地球物理学界的广泛重视，主要包括逆时成像条件的改进和成像结果的后续处理。例如Yoon等［13］提出了在零延迟互相关条件中加入波印廷矢量来消除成像噪声；Liu等［14］把全波场分解成单程波分量，并运用逆时成像条件结合这些单程波波场分量达到消除成像噪声的目的；Antoine等［15］采用最小二乘预测误差滤波器消除成像噪声；Zhang等［16］指出拉普拉斯算子滤波相当于成像波场角度域衰减；刘红伟等［17］指出在叠前对数据进行相位和振幅校正，在成像后运用拉普拉斯算子滤波法消除成像噪声；杨仁虎等［18］采用层状速度模型研究了速度百分比和位置误差对逆时结果的影响；陈可洋［19］研究了低频噪声的来源，并在叠加域、成像点域、共炮点域进行了拉普拉斯算子去噪分析；康玮等［20］比较了拉普拉斯算子、波印廷矢量法和上下左右行波分解法消除低频背景噪声的效果，认为拉普拉斯算子仍是目前最经济有效的处理手段；陈康等［21］采用四阶拉普拉斯算子有效地去除了低频成像噪声，并使滤波前、后子波的振幅和相位保持相对不变。

综上可知，在提高逆时成像精度方面的研究主要集中于低频逆时背景噪声的压制和理论模型研究。为此，本文从有偏移距逆时偏移脉冲响应出发，详细分析了低频背景噪声的形成机理及其压制思路，同时开展了高精度逆时偏移参数试验，并应用于实际陆上地震资料逆时偏移中，最终取得了较好的成像效果，这对复杂构造地震资料高精度逆时成像具有一定的指导意义。

1 逆时偏移脉冲响应研究

地震波逆时偏移脉冲响应研究是指导实际地震资料逆时偏移参数优化的一种重要途径。目前通常采用单层均匀介质模型来开展研究，本文以层状介质模型为例，能够更好地研究逆时成像技术的关键参数对成像结果精度的影响。文中采用时间2阶、空间16阶中心网格有限差分法［22］对标量声波波动方程进行有限差分离散近似以达到较高的数值模拟精度，同时在边界处采用10个网格厚度的内、外侧镶边法PML吸收边界条件，以充分吸收由人为截断边界引起的边界反射波能量［23－27］。

1.1 逆时成像条件对比

炮点位置采用主频为40Hz的雷克子波波形作为正演模拟部分的输入；检波点位置采用含5个不同幅值和相位、主频为40Hz、道长为1s的雷克子波波形的褶积法合成记录（图1a）作为逆时延拓部分的输入。炮、检点位置均在地表。层状介质模型横纵向大小为1km×1km；空间步长为5m×5m；上层介质速度为2 000m／s；下层介质速度为3 000m／s；炮检点间距为300m（图1b）。图1c和图1d分别为常规相关法逆时偏移有偏移距脉冲响应和上、下行波分离法逆时偏移有偏移距脉冲响应。

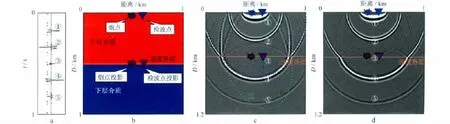
图1 检波点记录（a）、层状介质速度模型（b）、常规相关法逆时偏移脉冲响应（c）和上、下行波分离法逆时偏移脉冲响应（d）

分析图1c和图1d可知，有偏移距逆时偏移的脉冲响应为椭圆形状（①～⑤）。以检波点记录中子波波形④的脉冲响应为例，在上层介质中，分析图1c可知，Ⅰ为以炮点和检波点为焦点的椭圆曲线；Ⅱ为以炮点投影和检波点投影为焦点的椭圆曲线；Ⅲ为以炮点和检波点投影为焦点的椭圆曲线；Ⅳ为以炮点投影和检波点为焦点的椭圆曲线。在子波波形④的逆时偏移脉冲响应里，真正实现高精度地震波逆时成像的波场是曲线Ⅰ，其它3条脉冲响应曲线Ⅱ，Ⅲ，Ⅳ均为形成逆时噪声的波场能量。即正演部分和逆时延拓部分波场在遇到波阻抗界面时均会发生反射，这部分波场在应用逆时成像条件时是没有贡献的，但对于多次波等波场的延拓过程有贡献。该结论同样适合于倾斜界面，甚至更为复杂的介质情况。与此同时，由于脉冲响应遵循从炮点到成像空间某一位置与检波点到该成像空间位置的时间之和等于该子波波场在检波点记录中的时间，因此，在下层介质中，由于地层速度变大，单位时间内传播的距离增加，此时的脉冲响应波前面在高速层内传得更远些，反之亦然，且该波前面形状仍为椭圆形。为了有效压制低频干扰波场，我们引入了上、下行波波场分离逆时成像条件。该方法是在波场正演和逆时延拓过程中均将全波场分解为单程波场传播分量，即

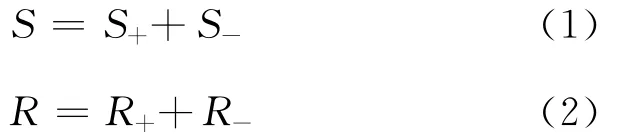
式中：S代表震源波场；R代表检波点波场；下标“＋”代表下行波场；下标“－”代表上行波场。根据互相关逆时成像条件，逆时成像结果为

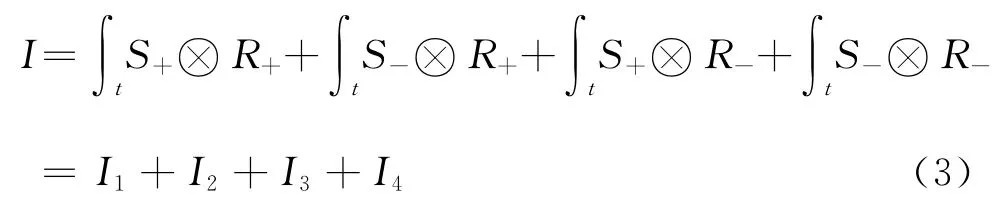
式中：符号“⊗”代表零延迟互相关计算；Ⅰ3代表震源下行波场和检波点上行波场的互相关结果，其等价于单程波偏移；Ⅰ2代表震源上行波场和检波点下行波场的互相关结果；Ⅰ1代表震源下行波场和检波点下行波场的互相关结果；Ⅰ4代表震源上行波场和检波点上行波场的互相关结果。其中，Ⅰ1和Ⅰ4分别包含了沿着射线路径震源波场一侧和检波点波场一侧的成像结果，因此，它们对逆时成像结果的低频噪声有贡献，需要将其去除，仅保留有效成像波场Ⅰ2和Ⅰ3，从而达到压制低频噪声和提高逆时成像精度的目的。应用上、下行波分离法逆时成像条件（图1d），在其脉冲响应中的曲线Ⅱ和Ⅲ的波场能量均得到了有效压制，对曲线Ⅳ的波场能量压制方法仍需深入研究，且该逆时成像条件可以在陡倾角处获得更好的成像效果（详见2.1节）。

1.2 速度平滑的影响

由于目前所应用的地震勘探相关理论仍是实际地球介质的一种近似，因此，根据实际地震资料通常较难获得准确的地层层速度模型，且常常存在一定的平滑特征。为此，开展了偏移速度平滑条件下的有偏移距叠前逆时偏移脉冲响应研究，采用的速度模型如图2a所示，该速度模型是在图1b的基础上进行平滑得到，采用的检波点记录和逆时偏移参数同1.1节。图2b和图2c分别为平滑速度情况下常规相关法逆时偏移有偏移距脉冲响应和上、下行波分离法逆时偏移有偏移距脉冲响应。

分析图2b和图2c可知，由于对偏移速度进行了平滑处理，原速度界面变得模糊，使得上层介质的速度沿着接近原速度界面方向逐渐增大，下层介质的速度沿着接近原速度界面方向逐渐减小。在速度平滑条件下，检波点记录中子波波形④的脉冲响应在下层速度较大介质中和平滑速度分界面处传播得更远一些，这一点也可从子波波形③的脉冲响应中观测到，此时子波波形③的脉冲响应波形已跨越了原始速度分界面位置。与此同时，在原速度分界面处，无论是采用常规相关法逆时成像条件，还是采用上、下行波波场分离逆时成像条件，其逆时偏移脉冲中均未见到明显的、形成逆时噪声波场能量的3条脉冲响应曲线Ⅱ，Ⅲ，Ⅳ，只有脉冲响应曲线Ⅰ波场得到较好的刻画。

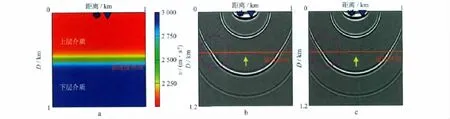
图2 速度平滑模型（a）及其常规相关法逆时偏移脉冲响应（b）和上、下行波分离法逆时偏移脉冲响应（c）

1.3 数值频散关系

虽然采用了高阶精度的有限差分算法和PML吸收边界条件，但是由于数值离散计算无法完全准确地代替连续的偏微分方程，总是存在一定的数值离散近似误差和计算机舍入误差，使得在实际逆时偏移数值计算时，对最大偏移频率或者偏移网格有一定的限制，两者是相互联系、相互影响的，其关系可依据波动方程数值频散关系的近似计算公式［26］：

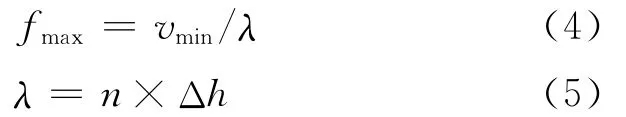
式中：fmax为最大偏移频率；vmin为最小速度；λ为地震波长；Δh为最大偏移网格；n为最短波长所占的空间节点数（与差分近似阶数相关，16阶差分时可取为2.5）。在vmin，Δh和n确定的情况下，根据（4）式和（5）式得到满足计算精度的最大偏移频率fmax；在vmin，fmax和n确定的情况下，根据（4）式和（5）式能够计算出满足计算精度的最大偏移网格Δh。

以偏移网格为例对数值频散影响计算精度的问题进行分析，采用的速度模型和检波点记录同1.1节。图3a到图3c的炮检点间距为300m；上层介质速度为2 000m／s；下层介质速度为5 000m／s。图3d到图3f为速度分界面垂直的情况，炮检点位于速度分界面两侧的对称位置，间距为500m；左侧介质速度为2 000m／s；右侧介质速度为5 000m／s。分析图3a和图3d可知，由于采用的最大偏移网格5m小于由公式（4）和公式（5）计算允许的最大偏移网格10m，因此，它们对应的逆时偏移脉冲响应中不存在数值频散现象，其计算精度较高；当横向空间网格变为20m时（图3b）或当纵向空间网格变为20m时（图3e），由于该偏移网格已大于由公式（4）和公式（5）计算允许的最大偏移网格10m，此时逆时偏移脉冲响应中就存在明显的数值频散问题，但该数值频散现象仅存在于速度低的一侧；当纵向空间网格变为20m时（图3c）或当横向空间网格变为20m时（图3f），由于该偏移网格大于由公式（4）和公式（5）计算允许的最大偏移网格10m，此时的逆时偏移脉冲响应中也会存在明显的数值频散问题，该数值频散现象不仅存在于速度低的一侧，在速度高的一侧也同样出现。分析原因可知，地震波数值频散存在传递性，只有当出现频散的介质为水平均匀介质层时不会进行传递（图3b和图3e），在其它任何介质分布情况下，只要地震波在低速层介质里传播时出现了数值频散问题，那么该数值频散现象就会向周围其它介质层（理论计算时该参数不会在该层出现数值频散问题）进行传递（图3c和图3f），因此，要提高逆时偏移成像的精度，就必须保证计算参数满足数值频散关系（4）式和（5）式的上限要求。

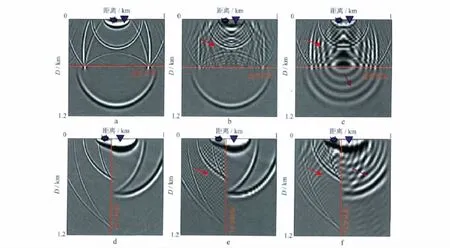
图3 不同速度分布、不同偏移网格情况下的常规相关法叠前逆时偏移脉冲响应

图4a和图4b分别给出了炮点和检波点位置互换前、后常规相关法叠前逆时偏移脉冲响应结果。分析图4可知，炮点和检波点位置互换前、后的脉冲响应结果完全一致，表明逆时偏移中的炮点和检波点位置具有可互换性，这为共检波点道集的逆时成像方法提供了理论指导，特别是炮点数量多和检波点数量少的VSP数据，可以大大减少逆时偏移的计算量，提高逆时偏移处理效率。

图4 炮点和检波点位置互换前（a）、后（b）常规相关法叠前逆时偏移脉冲响应

2 应用实例

根据脉冲响应理论分析结果，开展了国际标准二维TTI介质理论模型和实际三维地震资料的逆时偏移处理。

2.1 TTI介质理论模型

图5给出了采用国际标准二维TTI介质模型相应的原始单炮数据和速度模型进行的TTI介质叠前逆时偏移成像剖面（经拉普拉斯算子去噪处理）。其中，图5a采用的是常规相关法逆时成像条件；图5b采用的是上、下行波分离法逆时成像条件。分析图5a和图5b可知，经拉普拉斯算子去噪处理后，在采用常规相关法逆时成像条件的逆时成像剖面中，岩丘上边界连续性较差，在其两端陡倾角部位还存在一些虚假波场能量；而在采用上、下行波分离法逆时成像条件的逆时成像剖面中，岩丘边界刻画得连续且清晰，陡倾角处的虚假波场得到有效压制，同时其它成像位置同相轴的连续性也得到较大程度的提高。由此可见，采用上、下行波分离法逆时成像条件能够较大程度地压制由脉冲响应曲线Ⅱ和Ⅲ（图1c）形成的虚假波场干扰，从而达到提高逆时成像结果信噪比和精度的目的。

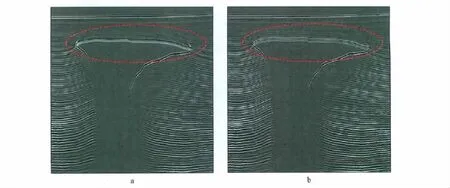
图5 TTI介质叠前逆时偏移结果

2.2 实际三维地震资料

研究区地震资料为陆上地震资料，其近地表条件较为复杂，浅层、陡倾角复杂构造成像是该区块的处理难点。工区采集面元为25m×25m；采用精细的地震速度优化建模技术和高保真地震资料预处理技术；深度域速度模型的最小速度为1 851m／s；要求的最大偏移频率为50Hz；采用上、下行波波场分离逆时成像条件，并应用GPU高性能并行计算技术提高逆时偏移处理效率。图6a为采用x和y方向的偏移网格为25m，深度z方向的偏移网格为10m时的实际单炮逆时偏移结果；图6b为采用x和y方向的偏移网格为12.5m，深度z方向的偏移网格为10m时的实际单炮逆时偏移结果。分析图6a可知，当偏移网格为25m时，在其单炮逆时偏移结果中可以明显见到数值频散现象，类似于逆时偏移脉冲响应中（图3c）的数值频散特征，且该数值频散现象一直传递至深层（局部放大可清晰识别），同时注意到浅层的数值频散现象最为严重，这对于逆时偏移成像结果的精度造成影响，其原因是根据公式（4）和公式（5）可以确定该工区最大允许的偏移网格为14.8m，而实际采用的偏移网格大于该上限值。分析图6b可知，将偏移网格减小到12.5m时，逆时偏移结果的数值频散现象得到了有效压制。

图7a为采用x和y方向的偏移网格为25m，深度z方向的偏移网格为20m，最大偏移频率为40Hz时的逆时偏移成像剖面（经拉普拉斯算子去噪处理）；图7b为采用x和y方向的偏移网格为12.5m，深度z方向的偏移网格为10m，最大偏移频率为50Hz时的逆时偏移成像剖面（经拉普拉斯算子去噪处理）。图7a和图7b中的逆时偏移参数均满足数值频散关系理论公式（4）和公式（5），因此，这两组参数的逆时成像结果是准确可靠的。对比图7a和图7b可知，当x和y方向的偏移网格越小，逆时偏移结果的横向分辨率越高；深度z方向的偏移网格越小，垂向分辨率越高，同时允许的最大偏移频率也越大，逆时成像剖面的细节特征刻画越清晰。因此，逆时偏移参数的优化选择有利于对中浅层和深层复杂构造成像区域的准确、清晰刻画。

3 结束语

我们详细研究了有偏移距叠前逆时偏移脉冲响应，深入分析影响逆时偏移成像精度的几个关键因素，并通过实际三维地震资料叠前逆时偏移参数的优化选择，取得了较好的应用效果，这对于中浅层乃至深层复杂构造地震资料高精度逆时成像方法具有一定的指导意义，通过研究得出如下结论：

1）相关法逆时成像条件的脉冲响应在其速度分界面处会形成4条椭圆形波场曲线（三维时为4个椭圆体）。这些波形曲线是以炮点、检波点及它们在速度界面的投影为椭圆焦点，且只有一条波场曲线是有效的成像波场，其它3条波场曲线是形成逆时偏移背景噪声的主要波场能量，它们是由地震波波场正向和逆时延拓过程中的上行反射波场引起。通过上、下行波波场分离逆时成像条件可以有效压制其中两条干扰波场曲线，但压制以炮点、检波点在速度界面投影为焦点的干扰波场曲线的方法仍有待进一步研究。同时，对偏移速度进行平滑处理，能够有效降低逆时背景噪声，但是以牺牲成像位置的准确性为代价。

2）地震波数值频散现象是影响逆时成像精度的重要因素之一。浅层的数值频散现象可以影响至深层，具有传递性。因此，逆时偏移参数（最大偏移频率和最大偏移网格等）的优化选择必须严格依据数值频散关系，同时还需保证数值迭代过程稳定，确保逆时偏移结果的准确可靠性。

3）逆时偏移中震源和检波点位置具有可互换性。这为共检波点道集，特别是检波点数少、炮点数多的井中地震或井间VSP资料的逆时偏移处理提供了理论方法指导，从而大大减小了计算量并提高处理效率，缩短处理周期。

［1］陈可洋.高阶弹性波波动方程正演模拟及逆时偏移成像研究［D］.大庆：大庆石油学院，2009 Chen K Y.High－order elastic wave equation forward modeling and reverse－time migration［D］.Daqing：Daqing Petroleum Institute，2009

［2］陈可洋.地震波逆时偏移方法研究综述［J］.勘探地球物理进展，2010，33（3）：153－159 Chen K Y.Reviews on seismic wave reverse－time migration methods［J］.Progress in Exploration Geophysics，2010，33（3）：153－159

［3］陈可洋.基于高阶有限差分的波动方程叠前逆时偏移方法［J］.石油物探，2009，48（5）：475－478 Chen K Y.Wave equation pre－stack reverse－time migration scheme based on high－order finite－difference［J］.Geophysical Prospecting for Petroleum，2009，48（5）：475－478

［4］陈可洋.两类共炮点域相关型叠前深度成像方法［J］.内陆地震，2012，26（1）：17－27 Chen K Y.Two kinds of correlation type pre－stack depth migration methods in common shot domain［J］.Inland Earthquake，2012，26（1）：17－27

［5］陈可洋.正演子波响应特征及逆时成像分析［J］.石油物探，2011，50（5）：455－462 Chen K Y.Seismic wavelet response characteristic and reverse－time migration analysis［J］.Geophysical Prospecting for Petroleum，2011，50（5）：455－462

［6］陈可洋.两种叠前逆时成像条件的比较［J］.油气藏评价与开发，2011，1（4）：6－11 Chen K Y.Comparison with two kinds of pre－stack reverse－time migration condition［J］.Reservoir Evaluation and Development，2011，1（4）：6－11

［7］陈可洋.高精度纯波震源数值模拟［J］.岩性油气藏，2012，24（1）：84－91 Chen K Y.High accuracy seismic pure wave source numerical simulation［J］.Lithologic Reservoirs，2012，24（1）：84－91

［8］陈可洋.地震波数值模拟中优化的通量校正传输方法［J］.内陆地震，2012，26（2）：169－179 Chen K Y.An optimized flux－corrected transport scheme in the seismic wave numerical simulation［J］.Inland Earthquake，2012，26（2）：169－179

［9］陈可洋.地震波旅行时计算方法及其模型试验分析［J］.石油物探，2010，49（2）：153－157 Chen K Y.Seismic wave travel－time computational method and its model experiment analysis［J］.Geophysical Prospecting for Petroleum，2010，49（2）：153－157

［10］陈可洋.时限时移相关法叠前逆时成像条件及其应用［J］.石油物探，2011，50（1）：22－26 Chen K Y.Time－limited time－shift correlation prestack reverse－time image condition and its application［J］.Geophysical Prospecting for Petroleum，2010，50（1）：22－26

［11］陈可洋.地震波数值模拟中差分阶数的边界效应［J］.高原地震，2011，23（1）：20－23 Chen K Y.Difference order’s boundary effect of the seismic wave numerical simulation［J］.Plateau Earthquake Research，2011，23（1）：20－23

［12］刘红伟，李博，刘洪，等.地震叠前逆时偏移高阶有限差分算法及GPU实现［J］.地球物理学报，2010，53（7）：1725－1733 Liu H W，Li B，Liu H，et al.The algorithm of high order finite difference pre－stack reverse time migration and GPU implementation［J］.Chinese Journal of Geophysics，2010，53（7）：1725－1733

［13］Yoon K，Marfurt K J.Reverse－time migration using the poynting vector［J］.Exploration Geophysics，2006，37（1）：102－107

［14］Antoine G，Bruno K，Biondo B.Least square attenuation of reverse time migration artifacts［J］.Expanded Abstracts of 76thAnnual Internat SEG Mtg，2006，2348－2352

［15］Liu F Q，Zhang G，Morton S A，et al.Reverse－time migration using one way wavefield imaging condition［J］.Expanded Abstracts of 77thAnnual Internat SEG Mtg，2007，2170－2174

［16］Zhang Y，James S.Practical issues of reverse time migration：true amplitude gathers，noise removal and harmonic source encoding［C］.CPS／SEG Beijing 2009International Geophysical Cofference ＆ Exposition，2009：5

［17］刘红伟，刘洪，邹振.地震叠前逆时偏移中的去噪与存储［J］.地球物理学报，2010，53（9）：2171－2180 Liu H W，Liu H，Zou Z，et al.The problems of denoise and storage in seismic reverse time migration［J］.Chinese Journal of Geophysics，2010，53（9）：2171－2180

［18］杨仁虎，常旭，刘伊克.叠前逆时偏移影响因素分析［J］.地球物理学报，2010，53（8）：1902－1913 Yang R H，Chang X，Liu Y K.The influence factors analyses of imaging precision in pre－stack reverse time migration［J］.Chinese Journal of Geophysics，2010，53（8）：1902－1913

［19］陈可洋.基于拉普拉斯算子的叠前逆时噪声压制方法［J］.岩性油气藏，2011，23（5）：87－95 Chen K Y.Pre－stack reverse－time noise suppressing method based on Laplacian operator［J］.Lithologic Reservoirs，2011，23（5）：87－95

［20］康玮，程玖兵.叠前逆时偏移假象去除方法［J］.地球物理学进展，2012，27（3）：1163－1172 Kang W，Cheng J B.Methods of suppressing artifacts in prestack reverse time migration［J］.Progress in Geophysics，2012，27（3）：1163－1172

［21］陈康，吴国忱.逆时偏移拉普拉斯算子滤波改进算法［J］.石油地球物理勘探，2012，47（2）：249－255 Chen K，Wu G C.An improved filter algorithm based on Laplace operator in reverse－time migration［J］.Oil Geophysical Prospecting，2012，47（2）：249－255

［22］陈可洋.标量声波波动方程高阶交错网格有限差分法［J］.中国海上油气，2009，21（4）：232－236 Chen K Y.High－order staggered－grid finite difference scheme for scalar acoustic wave equation［J］.China Offshore Oil and Gas，2009，21（4）：232－236

［23］陈可洋.地震波数值模拟中差分近似的各向异性分析［J］.石油物探，2010，49（1）：19－22 Chen K Y.Anisotropic analysis of difference approximation in seismic wave numerical modeling［J］.Geophysical Prospecting for Petroleum，2010，49（1）：19－22

［24］陈可洋.完全匹配层吸收边界条件研究［J］.石油物探，2010，49（5）：472－477 Chen K Y.Study on perfectly matched layer absorbing boundary condition［J］.Geophysical Prospecting for Petroleum，2010，49（5）：472－477

［25］陈可洋.边界吸收中镶边法的评价［J］.中国科学院研究生院学报，2010，27（2）：170－175 Chen K Y.Evaluation on the bordering method of the absorbing boundary condition［J］.Journal of the Graduate School of the Chinese Academy of Sciences，2010，27（2）：170－175

［26］陈可洋.网格剖分及其精度和计算量分析［J］.内陆地震，2011，25（1）：12－20 Chen K Y.Mesh Generation and its accuracy and computational amount analysis［J］.Inland Earthquake，2010，25（1）：12－20

［27］陈可洋.数值模拟的尺度调节机理［J］.内陆地震，2011，25（4）：321－328 Chen K Y.Scale adjusting mechanism on numerical simulation［J］.Inland Earthquake，2011，25（4）：321－328