异面预压铝蜂窝降低初始峰值力敏感性分析

王中钢，鲁寨军，夏 茜

（1轨道交通安全教育部重点实验室，长沙410075；2中南大学 交通运输工程学院，长沙410075）

蜂窝结构是理想的缓冲吸能材料，因优良的力学性能与较高的比吸能而深受工程人员青睐。目前国内外已针对蜂窝材料的力学行为[1－4］、吸能特性[5］、动态响应[6］等方面作了全面而系统的评估，并取得了相对可观的研究成果，为蜂窝产品的利用与开发奠定了坚实的基础，并已成功应用于车辆碰撞保护[7］、返回舱着陆器设计[8，9］等吸能相关工程中。作为缓冲吸能材料，它和常规的铝、钢、复合材料管件一样，在冲击力作用下发生塑性变形，将动能转化为结构变形能，吸收能量。然而，此类材料都有一个共同的特点，即在材料初始破坏时将产生一明显高于稳定段均值的初始峰值力，该力的反作用力是引起物件破坏与乘员伤害的直接原因之一。因此，有效抑制初始撞击力峰值大小，是保护结构设计的关键。通常可采用柔性结构和设置诱导式卸荷槽来降低初始撞击力峰值。柔性结构有橡胶、泡沫、棉被、薄铝等，但这种方法需要引入附加夹具，同时还可能引起碰撞偏心。因此，采用结构本身开设诱导式卸荷槽降峰方案成为众多工程人员的设计选择，这就相当于给结构预设了一初始“缺陷”。通常而言，蜂窝结构的内部缺陷对蜂窝结构的承载能力与吸能性能都会产生很大的影响[10］，而作为初始缺陷的一种，对蜂窝结构进行预压缩，却是降低初始撞击力峰值的有效途径之一。张安宁等[11］研究了预压缩处理后蜂窝纸板静态压缩特性，得出静态条件下峰值力明显减小的结论；尹汉锋等[12］将其应用于蜂窝装置的优化设计；美国著名蜂窝生产厂商Hexcel公司[13］也就其产品给出了预压缩处理的建议。预压缩处理方法已在准静态得到证实，对其动态条件下的力学行为有待深入，尤其是压缩深度、冲击速率等对预压结果的敏感性研究鲜见报道。认识并揭示动态条件下预压处理后铝蜂窝初始峰值力的特性变化是预压方法广泛推广的前提，因此，开展速率与压缩深度的敏感性分析具有重要的现实意义。

本工作通过建立预压蜂窝的全尺度显式非线性求解精细模型，研究不同预压深度的蜂窝在不同冲击速率下的峰值特性，为工程实际中蜂窝预压处理降低初始峰值力提供参考。

1 铝蜂窝结构特点及异面压缩力学特性

铝蜂窝是典型的二维周期性结构，其胞元通常可由胞元厚度t、边长h、边宽l以及内夹角θ四个参数来表达。本工作研究对象为正六边形蜂窝，在几何上自然满足h＝l，θ＝π／6。商用蜂窝多为粘胶后拉伸成形而得，这一工艺的必然结果是粘接边的胞壁的厚度是非粘接边的2倍，这也在细观上引起蜂窝结构的局部改变。其外观结构及胞元特点如图1所示。

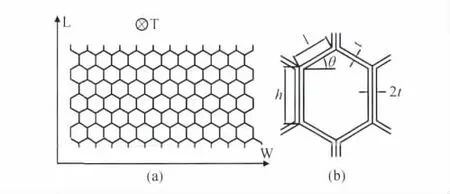
图1 铝蜂窝外观结构及胞元特点 （a）外观结构；（b）胞元Fig.1 Geometric characterization of aluminum honeycomb（a）appearance；（b）cell

铝蜂窝的共面压缩与异面压缩力学特性差异明显，但都会经历弹性（AB段）、塑性破坏（BC段）、渐近屈曲（稳定压缩CD段）、叠缩密实（DE段）四个基本过程。AC段胞元初始塑性破坏产生的峰值力是结构保护中不希望出现的，理想的吸能需求特性曲线应该是加载后直接进入稳定平台区段，即只有ACDE三段组成，其历程如图2所示。

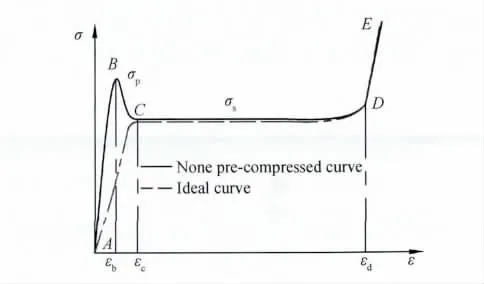
图2 蜂窝异面特性与理想需求曲线Fig.2 Curve of mechanical property and ideal one for honeycomb

2 预压缩数值模拟实现

2.1 预压缩数值模拟方法

蜂窝预压后，其预压部位几何形态各不相同，胞元信息错综复杂，直接借助建模工具构建其几何模型显然是不现实的，通过几何信息的再更新来实现是最合理的手段。具体方法如下：利用APDL快速构建蜂窝离散模型，通过设置预压阈值实现几何模型准静态预压缩，同时输出当前状态下蜂窝几何信息与单元信息；更新关键字文件（.k格式），去除预压后胞间预应力，重新设置加载方式与载荷大小等边界条件，进行动态求解，最后利用后处理软件提取计算结果。其具体流程如图3所示。

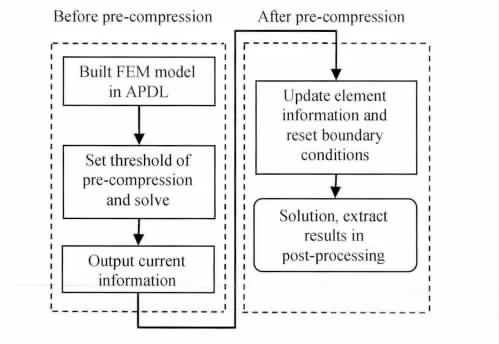
图3 蜂窝预压缩数值方法流程Fig.3 Process of numerical simulation method for pre－compressed honeycomb

2.2 预压缩数值模拟离散模型

所有的数值模拟工作均是在通用显式非线性软件包DYNA3D上完成的，仿真模型采用Belytschko－Tsay型壳单元构建蜂窝胞壁。为模拟动态冲击过程，仿真模型底端置于一固定的刚性墙上，另一移动刚性墙以恒定速率冲击仿真模型顶端；材料本构模型选用理想弹塑性模型[9，14］，选用 Cowper－Symonds模型[15］表达材料的应变率效应，选取因子分别为D＝1.7×106，p＝4。为防止胞间穿透，模型中所有边界均选用自动单面接触算法，摩擦因数为0.20。蜂窝基材为AL5052，其密度为2680kg／m3，弹性模量69.3GPa，泊松比0.33，屈服强度215MPa。文献[16］的胞元数敏感性分析结果表明当胞元数大于8×9以后其力学特性趋于稳定，故本工作选用9×11胞元数的蜂窝结构，其规格为t＝0.06mm，h＝l＝4mm，对应L方向宽90mm，W方向宽68mm，T方向高40mm。胞元每条边以及T向网格分别以胞元边长的1／8和1／10为离散长度进行离散，以精确捕捉异面压缩的褶皱；网格尺度对计算结果的影响已在允许范围之内。

2.3 预压效果实验对比

基于上述预压缩数值模拟方法，以恒定0.5m／s的速率模拟准静态加载的未预压、预压11mm两种试件，对比在万能材料力学性能试验机INSTRON上完成的同种蜂窝产品、同样几何尺寸、相同加载速率下预压缩11mm的结果，其应力－应变曲线如图4所示。本工作中应变计算的初始长度为预压后试件T方向的总高度，纵坐标皆为蜂窝强度，它由压缩载荷F与受载总面积S的比值计算得到，即σ＝F／S。蜂窝压缩的基本形态曲线均如图1所示，但为细观描绘峰值力变化特性，本文中所有图示均仅绘出压缩初始段及部分稳定段，以直观比较初始峰值的大小。实验结果与数值仿真结果如图4所示。

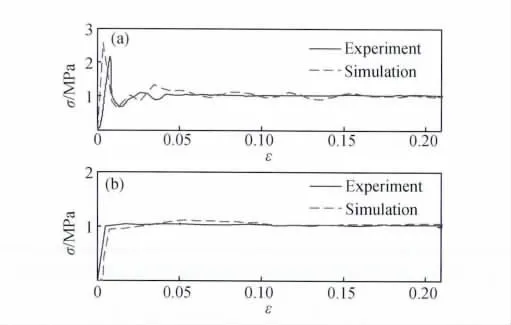
图4 准静态数值仿真与实验对比（a）未预压处理；（b）预压11mmFig.4 Comparison between numerical simulation and quasi－static experiment（a）none pre－compressed；（b）11mm pre－compressed

图4直观显现出预压缩处理在降低初始峰值力方面的良好效果，不仅维系了蜂窝稳定的平台区段，更主要是明显改观了初始撞击力峰值。预压后蜂窝的预压部位刚度减弱，引起蜂窝力流路径变化，蜂窝的初始峰值力明显消除，加载后直接进入到渐近屈曲段，直至密实。实验结果与数值计算结果的对比验证了数值模拟的可靠性。

3 预压缩敏感性分析

3.1 速率敏感性

铝蜂窝应用于不同的吸能场合时，其承受冲击的速率也不尽相同，预压缩后不同冲击速率下蜂窝动态响应特性有待评估。

选择与准静态实验一致的预压11mm的蜂窝试件进行不同冲击速率下的数值模拟，速率分别为代表准静态的0.5m／s，代表动态冲击的5，10，20，30，40m／s，分析冲击速率对预压后初始撞击力峰值的影响，模拟结果如图5所示。为直观比较，文中所有敏感性分析比较图示结果均对相应曲线进行了整体右移处理。

从图5可知，预压后蜂窝对速率十分敏感，准静态压缩与动态冲击时，其峰值特性差异明显。准静态条件下，预压后峰值力几乎不存在，而是直接进入了稳定压缩段。动态的5，10，20，30，40m／s依然出现了峰值力，但明显高于准静态加载情况，在速率高于20m／s后跃升尤为明显。

3.2 预压缩深度敏感性

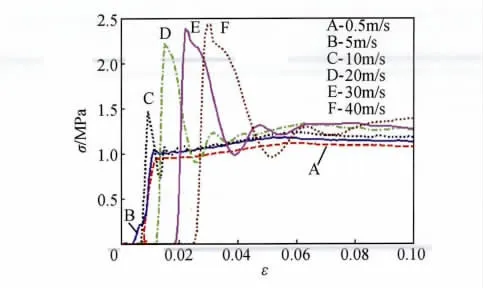
图5 不同冲击速率的初始峰值力比较Fig.5 Comparison between first peak forces at different velocities

对于异面压缩体现为渐近屈曲特性的蜂窝而言，其周期性褶皱必然引起力学特征量的周期性响应，因而预压量成为最为敏感的问题之一，不同预压程度的蜂窝能否出现初始压缩时刻的周期性力学响应，这需要开展压缩深度敏感性研究。从图4可知，蜂窝在ε＝0.15以后已明显进入稳定的渐近屈曲段。另一方面，对于胞壁而言，蜂窝的屈曲波长近似等于蜂窝胞元的边长[1］，对于t＝0.06mm，h＝l＝4mm的蜂窝产品，其屈曲波长近似等于4mm，因而预压缩量的样点选取从预压6mm至预压13mm区间段按1mm增量变化选取。图5结果表明冲击速率10m／s时，峰值特性变化明显，因而，压缩深度敏感性分析时采用10m／s的冲击速率，各计算结果如图6所示。

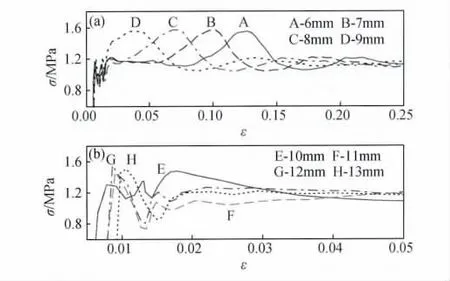
图6 不同预压量的比较（a）预压6～9mm；（b）预压10～13mmFig.6 Comparison between different pre－compressed honeycomb specimens（a）6－9mm pre－compressed；（b）10－13mm pre－compressed

由图6可知，不同预压量情况下，峰值特性不同。预压量低于10mm的蜂窝均出现二次峰值，且出现时刻对应的应变各不相同。而当压缩深度达到11mm及其以上时，在加载初始时刻即出现峰值力，继而进入稳定压缩段。观察各峰值发现，除预压10mm蜂窝峰值稍偏小外，其余试件峰值力近乎相等。预压量为10mm的蜂窝其初始峰值力出现了阶梯波动，处在两者的过渡阶段，其力学特性尚不稳定。而从6～13mm的整个预压过程来看，并未发现预压量与峰值力的周期对应现象，通过实验观测与数值模型发现（见图7），在蜂窝预压缩处理时，其局部刚度的改变不仅发生在紧随的压缩波周期内，还延拓至下一个屈曲周期，这与力学曲线反映结果相一致。由此可得，预压深度的理想周期性是不存在的。

图7 局部刚度减弱的延拓 （a）准静态实验；（b）数值仿真Fig.7 Continuation of local stiffness weakness（a）quasi－static experiment；（b）simulation

3.3 不同速率与预压量的整体敏感性

以上研究表明，预压后蜂窝的峰值力特性与预压缩量和冲击速率密切相关，因此，有必要研究不同预压量下不同速率冲击时，蜂窝的峰值力变化情况。分别以10，20，30，40m／s冲击未预压处理和预压缩量为6，7，8，9，10，11，12，13mm 的试件，其所得的应力－应变关系曲线如图8所示。

从图8可直观得到，所有预压后的峰值力均明显小于未预压前，预压13mm的蜂窝在40m／s冲击时峰值力仅为2.57MPa，明显小于未预压前40m／s的5.42MPa。不同预压量蜂窝其峰值力随冲击速率的增加总体呈增大趋势，尤其显现在10m／s跃升至20m／s时，其对应的峰值力增幅明显，20m／s后增幅变缓。在速率达到20m／s后，原来存在二次峰值的蜂窝，二次峰值依然存在，且在加载的初始时刻出现新的峰值力，并且该力已接近甚至高于二次峰值。此时，在吸能材料设计与选择的过程中需要考虑该峰值对结构产生的附加影响。在11mm以后蜂窝二次峰值消失，且压缩趋于稳定，建议按蜂窝胞元边长的3倍及其以上选取预压缩量。

4 结论

（1）铝蜂窝的预压缩数值模拟可通过几何信息与边界条件的再更新来实现，其对预压量与冲击速率两参数非常敏感。

图8 不同预压量下不同速率冲击应力－应变曲线（a）未预压；（b）预压6mm；（c）预压7mm；（d）预压8mm；（e）预压9mm；（f）预压10mm；（g）预压11mm；（h）预压12mm；（i）预压13mmFig.8 Stress－strain curves of different pre－compressed honeycomb at different impacting velocities（a）none pre－compressed；（b）6mm pre－compressed；（c）7mm pre－compressed；（d）8mm pre－compressed；（e）9mm pre－compressed；（f）10mm pre－compressed；（g）11mm pre－compressed；（h）12mm pre－compressed；（i）13mm pre－compressed

（2）预压后蜂窝在准静态与动态体现出不同的峰值特性；准静态加载时，蜂窝直接进入稳定压缩段，初始峰值力不复存在，预压处理效果明显。动态条件下，预压缩量的不同，预压后峰值特性也不同。若预压量低于某定值时，蜂窝先进入稳定压缩段，继而出现一相对较低的二次峰值，当达到或超过该定值后，峰值力特性趋于稳定，蜂窝二次峰值不再出现，但在加载初始时刻即出现峰值。蜂窝的预压缩过程中，局部刚度的改变不仅发生在紧随的一个压缩波周期内，还延拓至下一个屈曲周期中。理想的预压缩周期产生周期性峰值力的现象是不存在的。

（3）对出现二次峰值的预压蜂窝，二次峰值随冲击速率提高增加不明显，反而在速率达到20m／s后，在加载初始时刻出现新的初始峰值力，该力值甚至大于二次峰值。但二次峰值与预压后初始峰值均小于未预压处理的蜂窝初始峰值，峰值特性得到明显改观。

（4）考虑蜂窝作为主要吸能材料或结构时，应综合考虑速率条件与待保护物的耐受极限，选取合适的预压量，既确保峰值力在耐受极限内，又尽量避免二次峰值引起的附加破坏。建议按蜂窝胞元边长的3倍及其以上选取预压缩量。

[1]GIBSON L J，ASHBY M F.Cellular Solids：Structures and Properties[M］.Cambridge：Cambridge University Press，1997.93－169.

[2]WIERZBICKI T.Crushing analysis of metal honeycomb[J］.Int J Impact Eng，1983，1（2）：157－174.

[3]COTE F，DESHPANDE V S，FLECK N A，etal.The out－ofplane compressive behavior of metallic honeycombs[J］.Materials Science and Engineering：A，2004，380（1－2）：272－280.

[4]WU E，WU S.Axial crush of metallic honeycombs[J］.Int J Impact Eng，1997，19（5－6）：439－456.

[5]胡玲玲，余同希.惯性效应对蜂窝能量吸收性能的影响[J］.兵工学报，2009，30（增刊2）：24－27.HU Lin－lin，YU Tong－xi.Influence of inertia effect on the energy absorption of hexagonal honeycombs[J］.Acta Armamentarii，2009，30（S2）：24－27.

[6]王志金，邓子辰，周加喜.蜂窝夹芯圆柱壳在冲击内压作用下的轴对称动态响应[J］.西北工业大学学报，2010，28（3）：429－435.WANG Zhi－jin，DENG Zi－chen，ZHOU Jia－xi.Axisymmetric dynamic response of sandwich cylindrical shell with honeycomb core subject to internal shock pressure[J］.Journal of Northwestern Polytechnical University，2010，28（3）：429－435.

[7]ZINNO A，FUSCO E，PROTA A，etal.Multiscale approach for the design of composite sandwich structures for train application[J］.Compos Struct，2010，92（9）：2208－2219.

[8]陈金宝，聂宏，柏合民.月球着陆条件对铝蜂窝材料缓冲性能的影响[J］.机械工程材料，2008，32（1）：48－50，54.CHEN Jin－bao，NIE Hong，BAI He－min.Study of honeycomb on buffering performance of lunar lander[J］.Materials for Mechanical Engineering，2008，32（1）：48－50，54.

[9]王闯，刘荣强，邓宗全，等.铝蜂窝结构的冲击动力学性能的试验及数值研究[J］.振动与冲击，2008，27（11）：56－62.WANG Chuang，LIU Rong－qiang，DENG Zong－quan，etal.Experimental and numerical studies on aluminum honeycomb structure with various cell specification under impact loading[J］.Journal of Vibration and Shock，2008，27（11）：56－62.

[10]廖明顺，左孝青，潘晓亮，等.缺陷对蜂窝铝压缩变形机制及性能的影响[J］.材料导报，2005，19（12）：129－131.LIAO Ming－shun，ZUO Xiao－qing，PAN Xiao－liang，etal.Effect of defects on compression properties and deformation behaviour of aluminum honeycomb[J］.Materials Reviews，2005，19（12）：129－131.

[11]张安宁，童小燕，刘效云，等.预压缩处理蜂窝纸板静压缩特性试验研究[J］.包装工程，2006，27（6）：94－95，115.ZHANG An－ning，TONG Xiao－yan，LIU Xiao－yun，etal.Research on static compression properties of pre－compressed honeycomb paperboard[J］.Packaging Engineering，2006，27（6）：94－95，115.

[12]尹汉锋，文桂林，马传帅，等.蜂窝结构缓冲装置的优化设计[J］.中国机械工程，2011，22（10）：1153－1158.YIN Han－feng，WEN Gui－lin，MA Chuan－shuai，etal.Optimization design of cushion instrument of honeycomb structure[J］.China Mechanical Engineering，2011，22（10）：1153－1158.

[13]Hexcel Company.HexWeb®Honeycomb Energy Absorption Systems Design Data Report[R］.Stratford：Hexcel Company，2005.

[14]GUO X E，GIBSON L J.Behavior of intact and damaged honeycombs：a finite element study[J］.Int J Mech Sci，1999，41（1）：85－105.

[15]LU G X，YU T X.Energy Absorption of Structures and Materials[M］.Cambridge：Woodhead Publishing Limited，2003.268－278.

[16]SUN D Q，ZHANG W H，WEI Y B.Mean out－of－plane dynamic plateau stresses of hexagonal honeycomb cores under impact loadings[J］.Compos Struct，2010，92（11）：2609－2621.