2D－Cf／SiC复合材料缺口试件拉伸力学行为研究

郭洪宝，王 波，矫桂琼，刘永胜

（1西北工业大学 力学与土木建筑学院，西安710129；2西北工业大学 材料学院，西安710072）

连续纤维增强陶瓷基复合材料作为新一代高温热结构材料，在航空航天领域具有广阔的应用前景[1，2］，2D－Cf／SiC复合材料是其中具有代表性的一种超高温结构材料，它具有高比强度、比模量以及耐高温、热稳定性好等优点；克服了单一陶瓷材料脆性大的缺点，具有较好的断裂韧性，因此应用前景十分广阔[3］。随着Cf／SiC复合材料应用范围的扩大，为了满足复合材料构件连接的要求，需要在复合材料试件上开缺口，这势必会影响结构的力学性能；另外，Cf／SiC复合材料的制作工艺和力学性能与树脂基复合材料有较大的区别，因此需要对Cf／SiC复合材料缺口试件的力学性能进行研究。

大量研究者对2D－Cf／SiC复合材料的基本力学性能做了许多研究工作，熊伟等[4］、管国阳等[5］分别研究了2D－Cf／SiC复合材料的断裂韧性、失效判据；杨成鹏等[6］通过单轴拉伸和循环加卸载实验研究了2D－Cf／SiC复合材料的损伤演化过程和应力－应变行为，并建立细观力学模型对材料的损伤本构关系和极限强度进行了模拟预测。Wu等[7］通过高温真空环境下的拉伸蠕变实验，研究了不同温度对2D－Cf／SiC复合材料双边开半圆型缺口试件拉伸蠕变行为的影响；Ju等[8］通过影像相关实验和最小开方方法相结合得到了一种计算各向异性材料双边混合型缺口应力集中因子的简便实验方法；Ji等[9］通过三点弯曲实验研究了三维编织Cf／SiC复合材料单边缺口试件的断裂特性；侯军涛等[10，11］对2D－Cf／SiC复合材料双边开圆弧型缺口试件分别进行室温空气和高温真空环境下的单调拉伸和拉－拉疲劳实验，分析了环境温度对材料缺口敏感性、基体裂纹开裂应力、材料电阻和损伤断裂模式的影响以及试件在疲劳载荷作用下的S-N曲线、应力集中现象及损伤量变化情况。目前对2DCf／SiC复合材料双边缺口试件的拉伸力学行为研究还不多见，关于深入地讨论缺口试件应力应变集中问题的文献较少。

本工作通过实验分析和有限元模拟相结合的方法，研究了不同形状缺口对2D－Cf／SiC复合材料试件拉伸力学行为的影响，深入研究了不同形状缺口试件的应力应变集中现象、损伤演化进程和剩余强度影响因素。

1 试件和实验

1.1 试件

本工作所用的2D－Cf／SiC复合材料由西北工业大学超高温复合材料实验室制备，首先将T300炭纤维布叠层成二维编织预制体，经初步气相沉积（CVI）后，进行试件剪裁和开缺口加工，最后再经过多次CVI工艺沉积碳化硅基体，最终试件材料的密度约为2.0g／cm3。缺口试件长度为110mm，双边对称开缺口，缺口处最窄截面宽度均为6mm，厚度为3mm，每组试件各10件，标准拉伸试件采用狗骨型（实验段横截面宽度为10mm，厚度为3mm）。所有试件两端均粘贴铝制加强片防止试件夹持段被压溃。缺口试件具体几何形状和尺寸如图1所示。

图1 试件几何尺寸及应变片和引伸计位置（a）V型缺口；（b）半圆型缺口；（c）细线型缺口Fig.1 Specimens’geometry dimensions and locations of strain gauges and extensometer gauge（a）V shape；（b）half round shape；（c）hairline shape

1.2 实验

拉伸实验在INSTRON 5567试验机上进行，加载速率为0.3mm／min。通过在试件表面最小净截面方向上缺口边缘粘贴两枚1AA（应变电阻丝栅格长度和宽度均为1mm）应变片，用来采集拉伸过程中此局部区域材料的实时应变数据；试件缺口段材料整体变形通过引伸计测得，引伸计跨距为10mm。应变片粘贴位置和引伸计卡口位置如图1所示，两者测得的应变方向均与加载方向相同。

2 实验结果与分析

2.1 应力－应变行为

三种缺口试件和标准拉伸试件的拉伸应力－应变曲线如图2所示，其中应变数值均来自应变引伸计，应力数值取为最小净截面平均应力。图2中四条曲线的上升趋势各不相同，说明在相同应力水平下，三种缺口试件缺口段材料的拉伸变形大小不同，由小到大依次为：细线型、V型和半圆型，其中前两者相差不大，应力－应变曲线几乎重合；但是三种缺口试件的变形要明显小于标准拉伸试件。

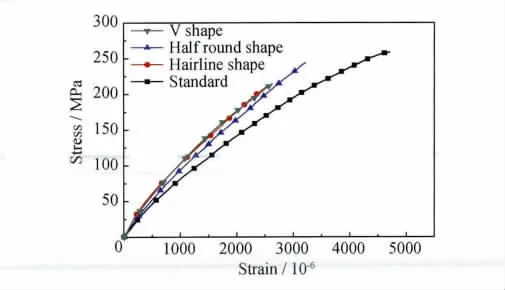
图2 拉伸试件应力－应变曲线Fig.2 Tensile stress－strain curves for specimens

缺口试件在拉伸过程中受最小净截面和应力应变集中的影响，试件轴向拉伸变形主要集中在最小净截面周围，其他区域材料变形较小。这是因为引伸计测得应变是位于卡口内材料的平均应变，因此测得的应变数值要小于同等应力水平下标准拉伸试件的应变值。同时因为应力集中的存在，拉伸过程中缺口边缘区域的材料会率先达到较高的应力水平，进而承担较大比例的拉伸载荷；而最小净截面上非缺口边缘区域材料的应力水平要略低于截面平均水平，此部分材料的轴向变形较小，也是造成引伸计测得的缺口试件拉伸轴向变形较小的原因。考虑到试件的CVI制备过程，缺口试件缺口段材料的表面积与体积的比值要远大于标准试件实验段材料对应比值，具有更有利的气相沉积环境，这会增加缺口段材料的基体密度和抗拉模量，也会减小其拉伸轴向变形。

2.2 应变集中及损伤失效分析

图3单独给出了三种缺口试件的拉伸应力－应变曲线，应变数值分别取自引伸计和1，2号应变片，应力数值为试件最小净截面平均应力。可以看出，在同一时刻，缺口边缘材料的应变数值要明显大于缺口段材料整体的应变水平，说明在整个拉伸过程中，缺口边缘存在明显的应变集中现象。

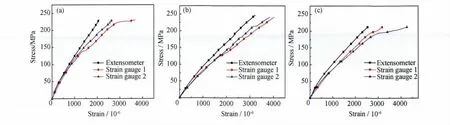
图3 缺口试件拉伸应力－应变曲线（a）V型缺口；（b）半圆型缺口；（c）细线型缺口Fig.3 Tensile stress－strain curves for notched specimens（a）V shape；（b）half round shape；（c）hairline shape

拉伸过程中，2D－Cf／SiC复合材料的应变数值与其损伤程度具有单调对应关系，所以通过试件局部材料的应变数据可以分析其损伤程度和损伤进程。由图3可见，在初始阶段，应变片对应两条曲线较光滑且基本重合，说明同一时刻1，2号应变片测得的应变值相差不大，双边缺口区域材料仍然保持着相同的应力－应变行为和损伤进程；当V型、半圆型和细线型缺口试件最小净截面应力分别达到102，125MPa和100MPa左右时，两条应变片曲线都开始出现不同程度的波动和偏差，但是曲线总体趋势基本相同。这是因为在实验初始阶段，虽然有应力集中的影响，但是缺口边缘区域材料的应力水平还比较低，并未发生严重的损伤破坏，对应的两条应力－应变曲线较光滑且基本重合。随着载荷的增大，缺口边缘区域的材料因为应力集中影响率先到达较高的应力水平而发生明显的损伤破坏，材料的应力、应变数值发生小范围突变，对应的曲线会出现相应的抖动。缺口处应力集中程度越高，其发生明显损伤破坏时对应的截面平均应力越低。拉伸过程中试件双边缺口周围材料的损伤失效进程基本同步，所以在实验后半段两条应变片曲线差异能够基本维持在一个恒定的范围内。随着载荷的不断增加，试件最小净截面上的材料损伤总量和损伤区域不断累加，最终贯穿整个截面，试件发生断裂破坏。

作为典型的连续纤维增韧陶瓷基复合材料，2DCf／SiC复合材料在损伤发生后，通过基体开裂、界面脱粘、纤维滑移和拔出等损伤模式会表现出非线性应力－应变行为，材料拉伸模量出现大幅下降[12］。受上述材料损伤特性的影响，当试件缺口边缘材料在应力集中作用下率先发生损伤时，将造成最小净截面上的应力重分布，降低率先损伤区域材料的应力水平[13］；这将有利于降低缺口边缘材料的应力集中程度，保证双边缺口周围材料损伤失效的同步性。

3 试件拉伸强度分析

试件尺寸和拉伸实验结果见表1。可以看到，缺口导致试件拉伸净强度出现了不同程度的下降。相比于标准试件，V型、半圆型和细线型缺口试件的拉伸净截面强度分别下降了20%，13.4%和21.3%左右。缺口试件强度数值的离散系数也略大于标准试件，这与其损伤失效过程的复杂程度有关，损伤失效过程越复杂，数据的离散性就越大。

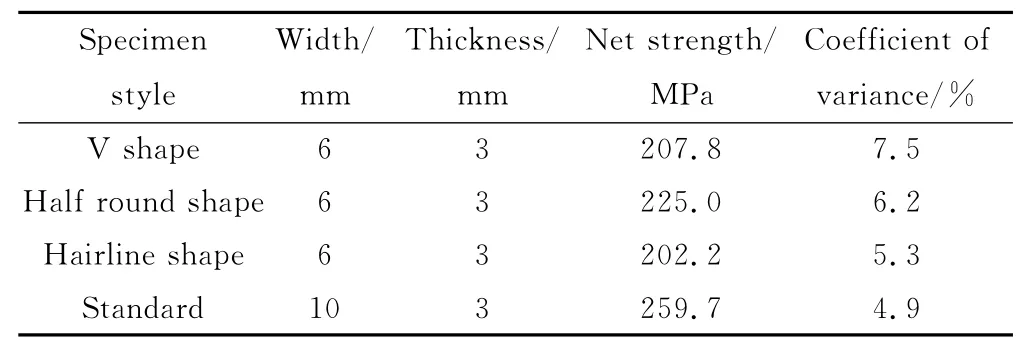
表1 试件尺寸和实验结果Table 1 Specimens’dimensions and experimental results

双边缺口的存在，使得缺口试件的损伤失效过程相比于标准试件变得更为复杂。通过缺口试件的应变分布情况可知，试件最小净截面上存在明显的应力集中现象，这将导致缺口边缘材料率先发生损伤和失效破坏。试件最小净截面上材料达到最大承载状态的非同步性，减小了试件的最终承载能力和拉伸净强度。同时，最小净截面使得试件存在确定的最弱截面，发生严重损伤破坏和断裂的材料区域主要集中在试件最小净截面。通过图4缺口试件的断口照片可以看出，断口与试件最窄截面基本重合，各层炭纤维布断裂位置基本一致，截面较平齐呈近似平面；经向纤维束拔出较短，断裂的位置都在临近纬向纤维束的边缘，拔出时也未携带纬向纤维束，说明试件损伤破坏过程受应力集中影响严重。

图4 缺口试件破坏断口（a）V型缺口；（b）半圆型缺口；（c）细线型缺口Fig.4 Fracture sections of notched specimens（a）V shape；（b）half round shape；（c）hairline shape

4 有限元模拟分析

通过模拟试件在实验初始阶段的应变场分布情况，可以表征试件拉伸过程中最小净截面上的应变分布情况。通过有限元软件ABAQUS建立缺口试件拉伸力学模型，采用等比例尺寸建模，材料类型为线弹性。材料力学性能利用9个工程弹性常数描述，参数数值通过材料基本性能实验及相关计算得到，数值大小如表2所示。试件模型一端固定，另一端采用面力加载方式，单元类型为C3D8R。图5中给出了V型、半圆型和细线型缺口试件沿载荷方向上的应变分量ε11的分布云图，对应的净截面平均应力均为50MPa。可以看出，半圆型缺口的应变集中影响区域最大，应变集中程度最低；V型缺口和细线型缺口的影响区域较小，且两者相差不大；细线型缺口引起的应变集中程度最严重。

表2 有限元模型材料工程弹性常数Table 2 The elasticity constants of the material in finite－element model

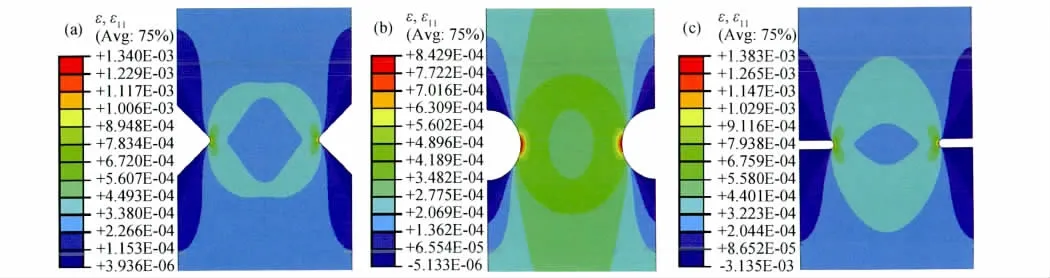
图5 缺口试件应变分布云图（a）V型缺口；（b）半圆型缺口；（c）细线型缺口Fig.5 Strain distribution of notched specimens（a）V shape；（b）half round shape；（c）hairline shape

依据有限元模拟结果，沿最小净截面方向上距离试件缺口边缘的距离设为X值，ε11设为Y值，得到试件最小净截面加载方向上的应变分布曲线如图6所示。将同等截面应力水平下的应变片测得数值与截面对应位置的模拟值进行对比发现，应变片测得数值与模拟结果偏差很小。微小偏差是因为有限元模型在计算过程中未考虑试件材料损伤的发生，而在实际情况中，试件材料在实验初始阶段就会出现轻微损伤。

图6 缺口试件最小净截面应变分布Fig.6 Strain distribution along the smallest net section of notched specimens

由图6可见，V型和细线型缺口试件的应变分布曲线基本重合，缺口边缘的应变数值很大，随着X的增大曲线快速下降并趋于平缓。半圆型缺口试件的应变分布曲线较为平缓，缺口边缘对应的数值较小，远离缺口处的数值要略高于前两者，此处模拟结果与实验引伸计测得结果吻合，即半圆型缺口段材料的拉伸变形要略大于V型和细线型缺口段材料。图6说明，在相同截面平均应力水平下，V型和细线型缺口试件最小净截面上受应变集中现象影响的区域要小于半圆型缺口试件，但是缺口边缘应变集中程度较高。通过最小净截面上最大应力（ε11max）与平均应力（ε11′）比计算得到V型、半圆型和细线型缺口试件的应力集中系数分别为3.02，1.84和3.09。由上可见，缺口引入的应力应变集中现象及其在试件最小净截面的分布情况，是影响试件损伤失效过程及拉伸净强度的决定性因素。

5 结论

（1）对于2D－Cf／SiC复合材料，双边缺口能够使试件产生明显的应变集中现象。在最小净截面具有相同平均应力水平下，缺口试件缺口段材料的轴向拉伸变形明显小于标准试件，其中V型和细线型缺口试件的轴向变形较小，半圆型缺口试件对应的轴向变形明显大于前两者。

（2）在拉伸过程中，细线型缺口试件缺口边缘区域材料率先发生明显失效损伤时对应的截面平均应力最低，V型缺口试件次之且与其相差不大，半圆型缺口试件对应应力值最高。2D－Cf／SiC复合材料在损伤发生后出现的非线性应力－应变行为和应力重分布，有利于降低缺口边缘区域材料的应力集中程度，保证双边缺口边缘区域材料损伤失效进程基本同步。

（3）相比标准拉伸试件，缺口试件因为缺口及其边缘应力集中现象的存在，使得其最小净截面整体材料损伤失效过程出现非同步性，试件最小净截面上的材料达到最大承载状态的非同步性是试件拉伸净强度下降的主要原因。

（4）通过有限元模拟发现，半圆型缺口引起的应变集中影响区域最大，应变集中程度最低；V型缺口和细线型缺口的影响区域较小，但是应变集中程度较高。试件缺口的应变集中程度越高，缺口边缘区域材料发生明显损伤破坏时对应的截面平均应力越低，对应的净截面拉伸强度值越小。

[1]邹武，张康助，张立同.陶瓷基复合材料在火箭发动机上的应用[J］.固体火箭技术，2000，23（2）：60－64.ZOU Wu，ZHANG Kang－zhu，ZHANG Li－tong.Application of ceramic matrix composite to rocket motor[J］.Journal of Solid Rocket Technology，2000，23（2）：60－64.

[2]张建艺.陶瓷基复合材料在喷管上的应用[J］.宇航材料工艺，2000，（4）：14－16.ZHANG Jian－yi.Ceramic matrix composite applications in nozzle[J］.Aerospace Materials and Technology，2000，（4）：14－16.

[3]李刚.二维编织C／SiC复合材料力学性能的试验研究[D］.西安：西北工业大学，2007.

[4]熊伟，矫桂琼，刘红霞.平纹编织C／SiC复合材料的断裂韧性[J］.硅酸盐学报，2008，36（8）：1057－1061.XIONG Wei，JIAO Gui－qiong，LIU Hong－xia.Fracture toughness of plain woven C／SiC composites[J］.Journal of the Chinese Ceramic Society，2008，36（8）：1057－1061.

[5]管国阳，矫桂琼，张增光，等.平纹编织C／SiC复合材料的失效判据[J］.硅酸盐学报，2005，33（9）：1100－1104.GUAN Guo－yang，JIAO Gui－qiong，ZHANG Zeng－guang，etal.Phenomenal failure criteria of a plain woven C／SiC composite[J］.Journal of the Chinese Ceramic Society，2005，33（9）：1100－1104.

[6]杨成鹏，矫桂琼，王波.2D－C／SiC复合材料的单轴拉伸力学行为及其强度[J］.力学学报，2011，43（2）：330－337.YANG Cheng－peng，JIAO Gui－qiong，WANG Bo.Uniaxial tensile stress－strain behavior and strength of plain woven C／SiC composite[J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43（2）：330－337.

[7]WU Xiao－jun，QIAO Sheng－ru，HOU Jun－tao，etal.Tensile creep behavior of notched two－dimensional－C／SiC composite[J］.Composites Science and Technology，2006，66（7－8）：993－1000.

[8]JU S H，CHUNG H Y，JHAO B J.Experimental calculation of mixed－mode notch stress intensity factors for anisotropic materials[J］.Engineering Fracture Mechanics，2009，76（14）：2260－2271.

[9]JI Gang－chang，QIAO Sheng－ru，DU Shuang－ming，etal.Threepoint bending fracture characteristics of three－dimensional－C／SiC with single－edge notch beam specimens[J］.Materials Science and Engineering：A，2008，483－484：123－126.

[10]侯军涛，乔生儒，韩栋，等.2D－C／SiC缺口试样的拉－拉疲劳损伤[J］.材料导报，2005，19（11）：140－143.HOU Jun－tao，QIAO Sheng－ru，HAN Dong，etal.Tensiontension fatigue damages of 2D－C／SiC notched specimens[J］.Material Review，2005，19（11）：140－143.

[11]侯军涛，乔生儒，韩栋，等.2D－C／SiC缺口试样的拉伸行为[J］.宇航材料工艺，2006，36（5）：44－49.HOU Jun－tao，QIAO Sheng－ru，HAN Dong，etal.Tensile behaviors of 2D－C／SiC notched specimens[J］.Aerospace Materials and Technology，2006，36（5）：44－49.

[12]熊伟.C／SiC复合材料断裂、损伤力学行为研究[D］.西安：西北工业大学，2009.

[13]HEREDIA F E，SPEARING S M，MACKIN T J，etal.Notch effects in carbon matrix composites[J］.J Am Ceram Soc，1994，77（11）：2817－2827.