船舶静态电场混合模型的逐步回归法优化求解

胡英娣，龚沈光，闫永贵

（1.海军工程大学兵器工程系，湖北 武汉 430033；2.海洋腐蚀与防护重点实验室，山东 青岛 266061）

0 引言

船舶水下静电场起源于船体不同材料之间的腐蚀电池及在船体上施行的各种防腐措施［1］，是船舶重要的目标特征信号，研究船舶静电场建模是实现电场深度换算和静电场隐身研究的基础，对船舶的探测和防护技术的发展有着重要意义。

由于船舶静电场的场源是船身及海水中的腐蚀与防腐电流，因此船舶腐蚀相关电磁场可以用位于船舶水下部分所占区域内的电偶极子产生的电磁场叠加来等效［2］，即目标船舶的静电场可以用若干个静态电偶极子产生的电场来模拟，这种建模方法称为等效源法。文献［3］采用位于船模纵向中心线上的一系列三分量电偶极子产生的电场来模拟船模水下静电场，此方法采用的模拟源数量很多，需要的测量数据量大，计算较为复杂。文献［4］提出可以采用一个水平电流线与若干个离散偶极子结合的混合模型对船模静电场进行了模拟，此模型较为简洁，具有较高的实用性，但是由于建模过程中模拟源的数量和位置往往难以确定，再加上测量信息不可避免存在误差，该文献中的模型求解方法通常不容易获得准确的解，极大影响建模精度。

本文针对此问题，提出基于逐步回归法的求解方法，对混合模型进行优化求解。

1 船舶静电场混合模型及逐步回归法

1.1 舰船静电场混合模型的典型形式

混合模型的形式为由一个线电流和若干个三轴电偶极子组成的阵列，每一个三轴电偶极子分别由x、y、z三个方向的电偶极子组成，因此每个位置上都会有三个相互垂直的电偶极距。它们在海水中的点Pj（xj，yj，zj）处产生的电场为各个模拟源产生的电场的叠加。

在已有的研究中，通常采用船舶静电场三分量场强数据来建模，研究表明，可以利用静态磁场的垂向分量实现船舶磁场的建模和定位［5］，类似的，可以只采用静电场的垂向分量来对船舶静电场进行建模，这样可以减少模型的维数，提高效率。因此模型方程可以表示为：

其中A表示方程组的系数矩阵，由于模型中任意方向偶极子源实际上是三个方向上的偶极子源的结合，因此矩阵A为M×（3 N＋1）维矩阵，即

X是待求的模拟源参数，即线电流的大小和各个偶极子的电偶极矩，构成3 N×1矩阵：

电场E是M×1矩阵

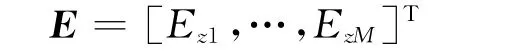
通过方程（2）求解出各个模拟源的参数是建模的关键，对于方程（2），由于船舶静电场建模中，测量数据向量长度通常大于模型向量长度，因此式（2）一般为超定方程，存在最小二乘解，

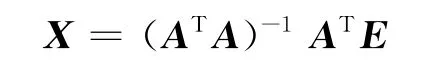
但是由于用模拟源法对船舶静电场进行建模时，通常是根据经验人为地设置模型中模拟源的个数和位置，而为了建模准确一般会选取尽量多的模拟源，因此模型中模拟源的个数有时会大于准确的模型所需要的模拟源个数，此时用最小二乘法求解的结果将包含冗余的模拟源，造成模型错误［6－7］。为避免这个问题，本文采用逐步回归法对模拟源的参数进行筛选再求解。

1.2 逐步回归法

逐步回归法［5］是以多元回归为基础，利用最小二乘法原理建立正规方程，求回归系数的一种回归方法。其基本原理是：将所要分析的n个自变量ai（i＝1，2，…，n）与因变量Y 的关系写为：

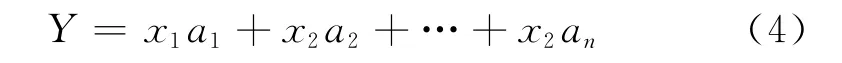
上式称为回归方程，逐步回归分析是在全部因素ai（i＝1，2，…，n）中按照对Y 作用的显著程度，由大到小逐个引入到回归方程（4）中，同时对回归的每一步进行显著性检验，因此当先引入的变量由于后面变量的引入而变得不显著时，则随时将其剔除，回归过程一直持续到没有显著的变量可以引入回归方程为止。

2 混合模型的逐步回归法优化

本文利用文献［4］提出的混合模型，在模型求解过程中用逐步回归法对模型中的模拟源进行选择优化，提高了模型的稳定性和准确性。

根据上文逐步回归法的原理，应用逐步回归法求解上述混合模型的步骤是：

1）计算式（3）中系数矩阵A的相关系数矩阵；

2）引入最显著的变量。计算（4）中各个变量ai与Y的相关系数，找出相关系数最大的变量，对它的偏回归平方和做显著性检验，若检验结果是显著的，则将其引入回归方程；

3）剔除不显著的变量。对回归方程（4）中已包含的变量逐个做显著性检验，若其偏回归平方和变为不显著，则剔除此变量，若显著性不变，则保留；

4）重复步骤2）和3），直到没有变量可以引入方程，也没有变量可以被剔除；

5）根据回归结果求解参数xi（i＝1，2，…，n）。

通过上述过程获得方程的解之后，代入方程中考察拟合误差，若误差较小则表明求解结果可用，若拟合误差仍然很大就说明建模失败，需要选择其他数据或重新建模。

3 仿真算例

为检验方法的性能，设计仿真实验，对一艘中型船舶进行建模。目标船舶的尺寸为：水线长117m，水线宽15.6m，吃水深度6.27m。该船舶船身涂层大致完好，只有铜制的螺旋桨和船头某处船壳有破损，船身上有4个对称布放的辅助阳极。由于船身产生腐蚀的区域主要是螺旋桨、船壳破损处及辅助阳极，因此将模型中线电流放置在船身纵向中心线上，长度为从螺旋桨到距离最远的辅助阳极的距离，偶极子均匀分布于线电流所在的直线上。在完成电场建模以后，分别采用最小二乘法和逐步回归法求解模型，并将结果与测量值相比较。在两个深度（h1＝10m，h2＝20m）上测量船舶在海水中的电场值作为仿真数据，由于客观条件限制，无法进行实船试验，因此静电场数据测量数据采用边界元法对目标船舶进行模拟的结果。边界元法通过分析船舶腐蚀和防腐情况，可以精确预测船舶腐蚀相关电磁场的分布，且已形成了成熟的商业软件，因此用边界元法模拟得到的数据相当于理想测量条件下的测量结果，可以用来进行换算和验证。

建立如图1所示的坐标系，以海平面为z＝0的平面，原点选在船舶的中心，z的正方向指向地心，x正方向指向船首，y正方向指向船的右舷。

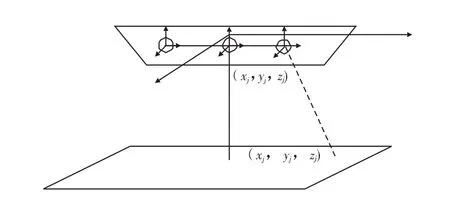
图1 电流线＋电偶极子建模Fig.1 Current line＋electric dipole modeling

假设模型中包含3个三轴电偶极子，那么混合模型由9个电偶极子和1个线电流源组成，用10m水深处的Ez数据建立模型并求解。在10m水深平面上选取平行于船舶纵向中心线的四条直线，直线坐标分别为y＝－6m，－2m，2m，6m，每条直线上选取12个测量点，一共48个测量点并用其Ez值建立模型。分别用最小二乘法和逐步回归法求解方程，解的误差如图2所示，图中实线表示电场测量值，＊号表示通过方程的解计算得到的电场值，可以看到对于此模型，用两种方法求解模型方程的结果都比较好。

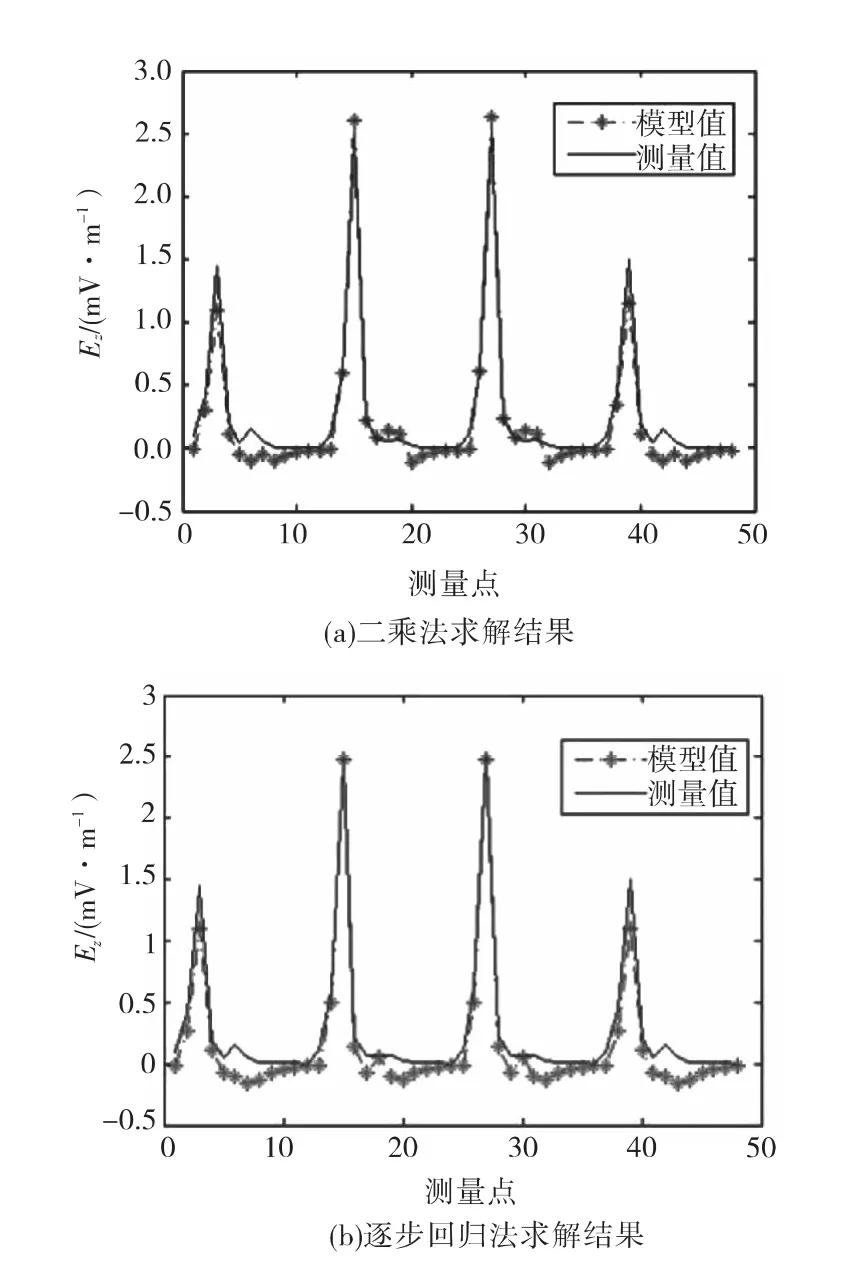
图2 模型求解误差示意图Fig.2 The fitting error curve of model

利用求得的模型计算20m深处一条直线（y＝－2）上的Ez，选取40个测量点的电场值作为第二组数据进行对比验证，将计算结果与测量值进行比较结果见图3。

图中可以看到两种方法求解模型并进行换算的结果与测量值符合较好，说明由3个三轴电偶极子和一个线电流组成的模型能很好地模拟目标船舶的静电场。这是由于测量点数据是由一个腐蚀情况较为理想的目标船舶所产生的，而模拟源的位置刚好位于船身腐蚀区域的位置。而在实际情况下，对船舶的静电场进行建模时往往并不清楚其腐蚀区域，而且像例子中的船舶这样，整个船身只有很小的一块区域被腐蚀的情形是不可能出现的，因此实际上对船舶静电场进行建模时往往采用尽量多的模拟源，以保证建模的精度。将模型稍作改进，增加偶极子源的数量，用上述两种方法求解模型并换算到第二组测量点处的值，换算值与测量值比较的结果如图4所示。当模型中包含5个均匀分布的三轴电偶极子即15个电偶极子，换算结果如图4所示，随着模型中偶极子数量的增加，用最小二乘法求解模型时，结果误差明显增大。这是由于最小二乘法求解的结果将包含了无效的模拟源，这就导致模型变得不准确。而逐步回归法则对模拟源进行筛选，剔除无效源，有效地保证了建模精度。

图3 Ez模型换算值与测量值对比曲线（3个三轴电偶极子）Fig.3 The contrsting curve of extrapolation result and theoretic result of Ez （the model of 3three components dipoles）

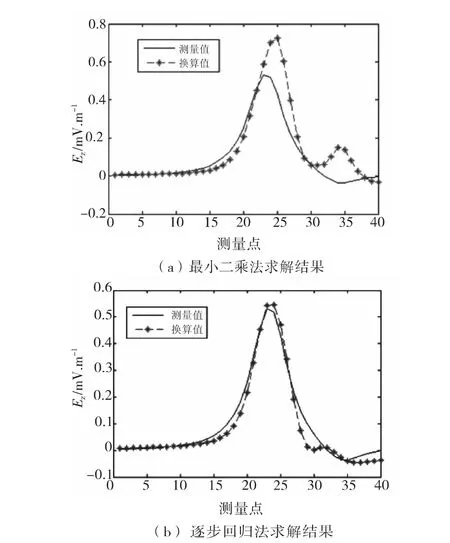
图4 Ez模型换算值与测量值对比曲线（5个三轴电偶极子）Fig.4 The contrsting curve of extrapolation result and theoretic result of Ez （the model of 5three components dipoles）

4 结论

本文基于逐步回归法提出了船舶静态电场建模的优化求解方法。该方法在模型求解过程中通过逐步回归法对偶极子的偶极矩参数进行优化选择，剔除对模型不重要的偶极矩，得到符合船舶静电场特征的模型，避免了人为设置静电场模型的弊端。

仿真结果显示逐步回归法结果在模型中模拟源数量较多时建模准确度远大于最小二乘法，表明本文的方法建模具有较高的精度。

［1］林春生，龚沈光.舰船物理场［M］.北京：兵器工业出版社，2007：237－242.

［2］彭祖赠.数学模型与建模方法［M］.大连：大连海事大学出版社，1997：237－242.

［3］刘胜道.舰船水下电场的测试技术与电偶极子模型研究［D］.武汉：海军工程大学，2002.

［4］陈聪，龚沈光，李定国.基于电偶极子的舰船腐蚀防腐相关静态磁场研究［J］.兵工学报，2010：31（1），113－118.CHEN Cong，GONG Shenguang，Li Dingguo.Research on the static magnetic field related with corrosion and anti－corrosion of ships based on the electric dipole model［J］.Introducing Journal of China Ordnance，2010，31（1）：113－118.

［5］陈聪，李定国，龚沈光.舰船水下标量电位的混合建模研究［J］.武汉理工大学学报（交通科学与工程版），2010：34（6），1117－1120.CHEN Cong，LI Dingguo，GONG Shenguang.The sduty of mixed modeling of ship's underwater electric potential［J］.Journal of Wuhan University of Technology（Transportation Science ＆Engineering），2010，34（3）：1117－1120.

［6］王金根，龚沈光，刘胜道.磁性目标的高精度建模方法［J］.海军工程大学学报，2001，13（3），49－52.WANG Jingen，GONG Shenguang，LIU Shengdao.High accuracy method for modeling magnetic object［J］.Journal of Naval University of Engineering，2001，13（3）：49－52.

［7］杨明明，刘大明，连丽婷.基于磁场梯度的船舶磁场模型［J］.舰船科学技术，2008，30（5）：95－97.YANG Mingming，LIU Daming，LIAN Liting.Vesselmagnetic field model based on magnetic gradient［J］.Ship Science and Technology，2008，30（5）：95－97.