基于最小二乘拟合的地磁场测量误差补偿方法

范淑瑞，王晓峰，张 合

（南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094）

0 引言

地磁场是天然存在的物理场，在地球近地空间连续分布且非常稳定，可作为载体导航和姿态检测技术的理想基准。磁传感器作为测量地磁场的敏感元件，具有体积小、响应快、成本低、抗高过载等优点，因此地磁导航技术在军事领域和国民经济生活中都得到非常广泛的应用［1－4］。

地磁场是矢量场，需要采用多个正交配置的磁传感器，才能够测量出地磁场矢量的大小和方向。但是，由于制造技术和工艺水平的限制，各个磁传感器之间不可能完全正交，并其各自的性能也存在差异，从而导致地磁场的测量中不可避免地存在着误差。文献［5］和［6］针对磁罗盘中的三轴磁传感器误差，建立了误差模型，并研究了其误差补偿方法，但是其必须依赖高精度无磁转台提供方向基准。文献［7］虽然省去了转台，但是其需要依赖磁罗盘的六个立方体平面提供方向基准。这两种方法都无法摆脱对外部基准的依赖，不可避免地引入对准误差和安装误差，并且补偿过程也较为复杂。

为了能够不依赖外部基准，准确方便地实现对地磁场测量系统误差的补偿，提出了基于最小二乘拟合的地磁场测量误差补偿方法。

1 三轴地磁场测量误差模型

1.1 地磁场测量误差分析

以霍尼韦尔公司的磁阻传感器HMC1021和HMC1022构成一个组合式三轴正交的磁传感器，三轴地磁场信号由模拟数字转换器进行采样，然后发送到上位机。

3轴地磁场测量系统的误差主要有非正交误差、标度误差和偏移误差等。非正交误差是由于HMC1021的敏感轴与HMC1022的两个敏感轴之间以及HMC1022的两个敏感轴之间不完全正交而引起的误差。标度误差是由于3个敏感轴方向上的灵敏度和模拟电路的增益不一致而引起的误差。偏移误差是由于磁传感器和模拟电路的电气参数不对称导致输出信号发生偏移而引起的误差［8－9］。

1.2 地磁场测量误差模型

以HMC1021的轴分别作为X轴，HMC1022的两个轴分别作为Y轴和Z轴，理论上这三个轴应相互正交，实际上这三个轴并非完全正交。假设磁传感器的X轴与理想测量方向一致。如图1所示，OXYZ为磁传感器的理想坐标系（正交坐标系），三个坐标轴方向为磁传感器的理想测量方向；OXsYsZs为磁传感器的实际坐标系（非正交坐标系），三个坐标轴方向为磁传感器的实际测量方向；坐标系原点O为磁传感器的中心，OXs与OX 重合。u1、u2和u3为地磁传感器的三个非正交误差角，其中u1为OY与OYs的夹角，u2为OZs在OYZ面的投影与OZ的夹角，u3为OZs与该投影的夹角。

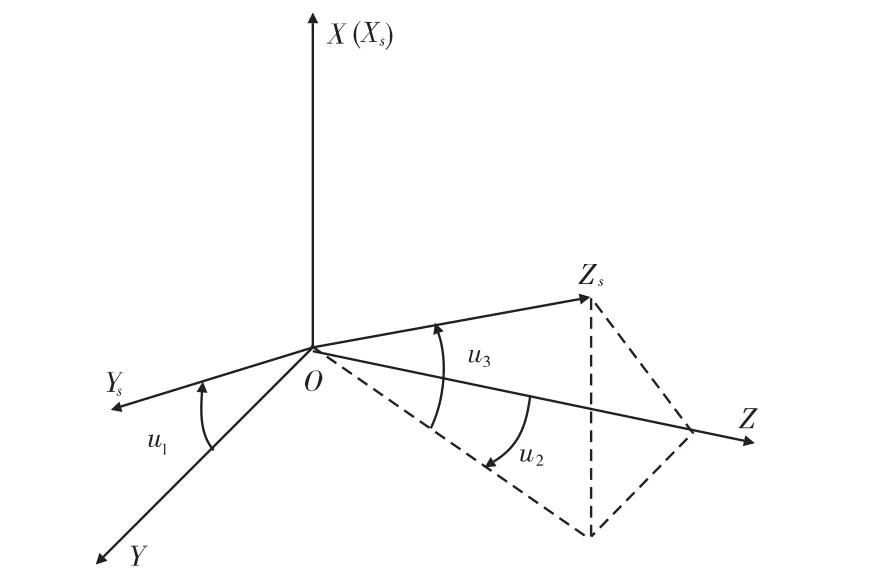
图1 磁传感器坐标系图Fig.1 The megnetic sensor coordinate system

假设地磁场矢量在OXYZ坐标系中为H，磁传感器输出的矢量为Hs，那么H与Hs转换关系［8，10］

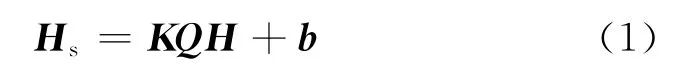
式（1）就是组合式三轴地磁场测量系统的误差模型。

矩阵K和Q通常均为可逆矩阵，如果已知模型中与磁传感器偏移误差、标度误差和非正交误差有关的9个误差系数，便可以得到真实的地磁场矢量

式中P＝ （KQ）－1＝Q－1K－1。

对于三轴地磁场测量系统的误差系数的求解，通常需要借助外部参考基准进行。利用外部设备提供精确的姿态信息，通过测量若干不同姿态下的三轴地磁场分量，然后根据不同姿态间的夹角关系，直接计算出磁传感器的误差系数。文献［5］和［6］依靠三轴转台提供姿态信息，文献［7］则依靠立方体的6个平面提供姿态信息，由于外部姿态角的基准信息与误差系数的计算结果直接相关，因此这种方法对外部设备的精度和地磁场测量系统的装配精度都有很高的要求，需要非常专业的设备或工具才能进行。

地磁场是稳定的均匀磁场，在某点附近可以认为地磁场矢量是恒定不变的，若能将外部参考基准转化为地磁场强度，便可在没有外部参考信息的条件下实现对地磁场测量系统误差的补偿。如果的地磁场强度为H，那么＝H。我们可以将式（2）转化为［11－12］

式中D＝PTP为对称矩阵。

令磁传感器输出的地磁场矢量Hs＝［x y z ］T，对式（3）展开并进行整理可得［12－13］

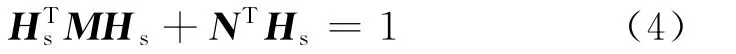
2 地磁场测量误差补偿方法

如果磁传感器的一组测量数据为［xiyizi］T， 其 中 i ＝ 1，…，n， 令 υ ＝［a b c d e f gh k ］T和ri＝［xi2yi2zi22xiyi2xizi2yizixiyizi］，那么可将椭球方程式（4）转化为一般形式

式（5）符合最小二乘法的基本方程形式，利用最小二乘拟合方法可以得到矢量υ，也就等于得到式（4）中的各个系数，由此可以得到

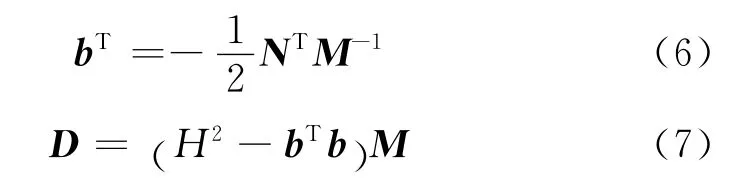
式中地磁场强度H可利用国际地磁参考场（International Geomagnetic Reference Field，IGRF）模型计算得到。然后，由式（6）可以计算出磁传感器的3个偏移误差系数。对式（3）中的D＝PTP进行展开，并结合式（7），可以通过代数运算可以得到与标度误差和非正交误差相关的6个系数。已知磁传感器的9个自身误差系数，根据式（2）便可以对地磁场测量系统进行误差补偿。

地磁场测量误差补偿的具体步骤可以归纳为：

1）数据采集：采集的地磁测量系统输出数据，同时把地磁场的采样数据实时发送到上位机。

2）拟合误差系数：利用三轴磁传感器的采样数据，根据式（5）（6）（7）采用最小二乘拟合方法进行计算式（4）中与误差系数相关的9个矩阵系数。

3）误差校正：根据已知的矩阵系数，计算地磁场测量系统误差模型中的9个误差系数，然后利用式（2）对地磁场测量系统进行误差补偿。

可以看到，在地磁场测量系统误差补偿的整个过程中，误差系数的求解与系统的姿态信息并没有任何关联，因此该补偿方法不需要依赖外部参考基准。

3 地磁场测量系统实验

为了验证补偿方法的有效性，建立地磁测量实验系统，将组合式三轴地磁场测量系统放置于均匀纯净的地磁场环境中，上电之后，分别绕不同的方向转动地磁场测量系统，同时把地磁场的采样数据实时发送到上位机。

将采集输出地磁测量系统的三路输出信号（每个方向为1 000个采样点），根据第2章中的补偿方法，得到地磁测量系统的3个标度误差系数分别为1.087、1.062和0.945，3个偏移误差系数分别为－443nT、386nT和－364nT，3个非正交误差角的角度值分别为1.43°、0.54°和1.12°。

将得到的9个误差系数装载到地磁场测量系统的内部程序中，对地磁场采样数据进行误差补偿，并将补偿前后的数据全部发送到上位机，在地磁测量系统绕不同方向旋转时，补偿前后的地磁场强度变化如图2所示。由图2可以看到，在补偿之前，由于存在较大的误差，测量的地磁场强度波动非常大，而补偿之后，地磁场强度大幅地减小，基本变成一条直线，与实际情况一致。通过对地磁场测量系统进行误差补偿，其地磁场强度的均方根误差由补偿前的4267nT减小到补偿后的224nT。

由此表明，地磁场测量系统的补偿方法能够快速有效减小其自身存在的各种误差，并且不需要依赖外部基准。

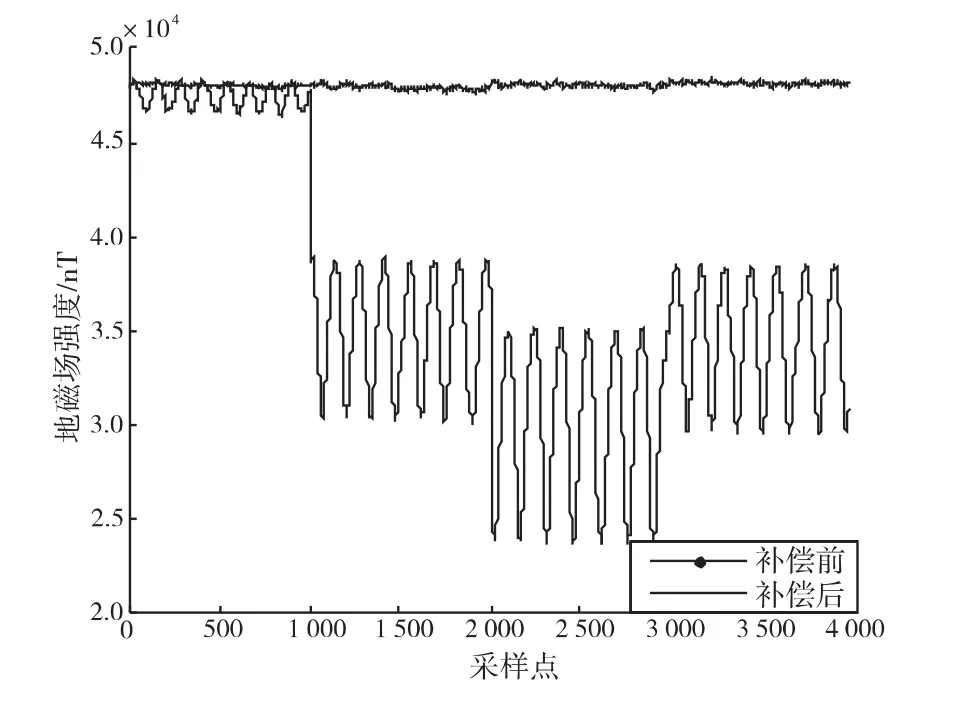
图2 补偿前后的地磁场强度Fig.2 The megnetic field strength before and after compensation

4 结论

针对地磁场测量系统需要依赖外部基准来进行误差补偿的问题，提出了了基于最小二乘拟合的地磁场测量误差补偿方法。该方法首先建立地磁测量误差模型，然后利用最小二乘法拟合得到地磁误差的椭球系数，最后将椭球系数转化成矩阵系数并对地磁测量数据进行校正。实验表明，利用最小二乘方法拟合得到能够准确计算出地磁场测量系统误差模型的9个系数，不需要依赖外部基准，便能准确、方便、快速地对地磁场测量系统进行误差补偿。

［1］杨云涛，石志勇，关贞珍，等.地磁场在导航定位系统中的应用［J］.中国惯性技术学报，2007，15（6）：686－692.YANG Yuntao，SHI Zhiyong，GUAN Zhenzhen，et al.Application of geomagnetic field in navigation and localization system［J］.Journal of Chinese Inertial Technology，2007，15（6）：686－692.

［2］杨荣军，王良明，修观，等.基于磁强计测量的滚转弹药姿态估计［J］.海军工程大学学报，2011，23（5）：108－112.YANG Rongjun，WANG Liangming，XIU Guan，et al.Attitude estimation of rolling－munitions using magnetometer［J］.Journal of Naval University of Engineering，2011，23（5）：108－112.

［3］Johnson，Lyle H.Kurschner，Dennis L.Roll orientation using turns－counting fuze［P］.EP，1813905，2007－08－01.

［4］Caruso.Michael J.Applications of magnetoresistive sensors in navigation systems［EB／OL］.［2013－04－08］http：／／www.docin.com／p－4543666316.html.

［5］Vcelak J，Ripka P，Kubík J，et al.AMR navigation systems and methods of their calibration［J］.Sensors and Actuators A.2005，123－124：122－128

［6］Vcelak J，Ripka P，Platil A，et al.Errors of AMR compass and methods of their compensation［J］.Sensors and Actuators A.2006，129（1－2）：53－57.

［7］孙宏伟，房建成，李艳.椭圆拟合方法在磁罗盘罗差校准中的应用［J］.光学精密工程，2009，17（12）：3034－3039.SUN Hongwei，FANG Jiancheng，LI Yan.Application of ellipse fitting method to calibration of magnetic compass deviation［J］.Optics and Precision Engineering，2009，17（12）：3034－3039.

［8］彭建飞，高启孝，夏学知.应用两步回归迭代算法校正数字式磁罗经误差［J］.舰船电子工程，2006，26（1）：137－140.PENG Jianfei，GAO Qixiao，XIA Xuezhi.Using two－step regression iterative algorithm in calibrating digital magnetometer＇s error［J］.Ship Electronic Engineering，2006，26（1）：137－140.

［9］黄学功，王炅.地磁信号检测系统误差分析与补偿方法研究［J］.兵工学报，2011，32（1）：33－36.HUANG Xuegong，WANG Jiong.Error Analysis and Compensation Methods for Geomagnetic Signal Detection System［J］.Acta Armamentarii，2011，32（1）：33－36.

［10］Honeywell Inc.1－and 2－Axis Magnetic Sensors［EB／OL］.［2013－04－08］http：www.Magnetic.sensors.com.

［11］Dorveaux E，Vissière D，Martin A，et al.Iterative calibration method for inertial and magnetic sensors［C］／／Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference.Shanghai.2009：8296－8303.

［12］Foster C，Elkaim G.Extension of a two－step calibration methodology to include nonorthogonal sensor axes［J］.Aerospace and Electronic Systems.2008，44（3）：1070－1078.

［13］Munschy M，Fleury S.Scalar，vector，tensor magnetic anomalies：measurement or computation［J］.Geophysical Prospecting，2011，59（6）：1035－1045.