ARIMA模型在地区GDP预测中的应用研究

刘明鼎

(青岛理工大学 琴岛学院，山东 青岛 266106)

ARIMA模型在地区GDP预测中的应用研究

刘明鼎

(青岛理工大学 琴岛学院，山东 青岛 266106)

在时间序列分析理论的基础上，以山东省2007年第一季度到2011年第四季度的GDP总值为基础,利用SPSS软件，对数据进行时间序列分析，建立时间序列分析模型，并对模型进行检验。利用建立的模型对山东省在2012年的GDP的增长趋势做出预测。

时间序列分析；ARIMA模型；GDP；预测

一 ARIMA模型的建立和检验

1.模型的描述。

ARIMA(p,d,q)模型对GDP进行预测本质上是先对非平稳的GDP历史数据Yt进行d次差分处理得到新平稳数列Xt，将Xt拟合到ARMA(p,q)模型中，然后再还原d次差分，这样便可以得到Yt的预测数据。其中，ARMA(p,q)的一般表达式：

Xt=φ1Xt-1+…+φpXt-p+εt-θ1εt-1-…

-θqεt-q,(tZ)

(1)

式中，前半部分为自回归部分，p(p≥0)为自回归阶数，φ1,φ2,…φp为自回归系数；后半部分为滑动平均部分，q(q≥0)为滑动平均阶数，θ1,θ2,…θq为滑动平均系数；Xt为GDP数据相关序列[4]。

当q=0时，该模型成为AR(p)模型：

Xt=φ1Xt-1+…+φpX1-p+εt,(tZ)

(2)

当p=0时，该模型成为MA(q)模型：

Xt=εt-θ1εt-1-…-θqεt-q,(tZ)

(3)

2.GDP增长预测建模流程。

(1)取基本数据并进行数据处理。

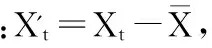
(2)ARMA模型的识别。

(4)

(5)

根据上面方法得到的计算结果，并依据下表的模型识别原则，确定X't符合的模型。

表1 ARIMA(p,q)模型识别原则

(3)参数估计和模型定阶。

参数估计和模型定阶是建立GDP预测模型的重要环节，二者相互影响。在模型识别的基础上，利用最小二乘估计法或极大似然估计法等对ARMA(p,q)模型的未知参数，即自回归系数、滑动平均系数和白噪声方差进行估计，得出结果后利用AIC、BIC准则进行模型定阶。

(4)模型检验。

首先要检验模型是否满足平稳性和可逆性，也就是要符合下面的式(6)和式(7)的要求：

(6)

(7)

然后再判断模型的残差序列是否为白噪声，若不是，则需要重新进行模型识别；若是，则通过检验，从而得出合理的预测模型：

(8)

(5)GDP预测。

根据得到的预测模型对X'进行预测，并考虑前面所进行的d次差分，还原为GDP数据Yt的预测结果。

二 基于ARIMA 模型预测山东经济发展前景

1．数据处理。

在山东统计信息网上，可以得到从2007年到2011年山东省各个季度的GDP数据。

利用spss软件可以得到数据的散点图，并找出数据的近似变化曲线，如图1：

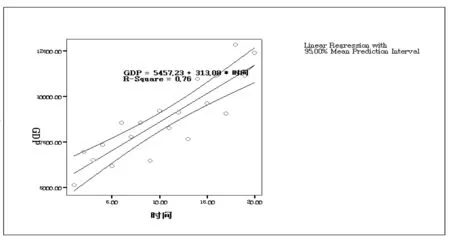
图1 散点图

从图1中，可以看出该时间序列的数据比较分散，图中给出了在95%的置信区间内的回归方程：GDP=5457.23+313.08*时间，根据方程求得2012年各季度的GDP为：

表2 2012年各季度的GDP

通过计算结果可以看出，所得到的GDP数据各季度的增长速率在3%左右，而我们通过在山东统计信息网上得到的以前各季度GDP的增长速率为10%左右，该回归方程可能不适合我们对时间序列进行预测，偏差比较大，所以需要对时间序列进行基本数据处理，利用ARIMA模型对时间序列进行分析和预测。利用Eiews软件对时间序列GDP绘制线形图(图2)：

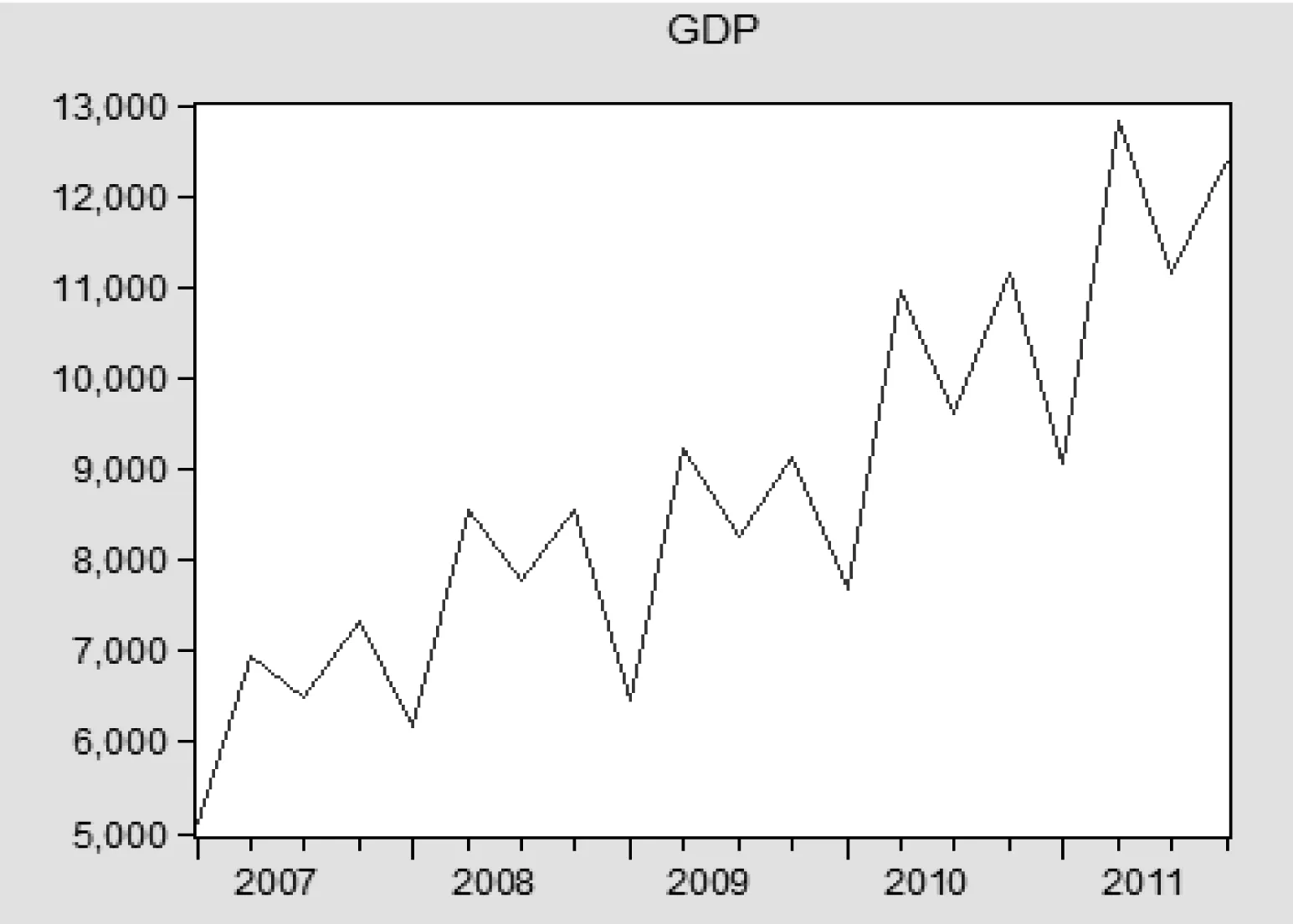
图2 线形图

从线形图可以发现，该时间序列具有明显的线性趋势，是非平稳的，而ARIMA模型建模的基本条件就是要求待预测的时间序列满足平稳的条件，即个体值要围绕序列均值上下波动，不能有明显的上升或下降趋势，如果出现上升或下降趋势，需要对原始序列进行差分平稳化处理，因此需要对被测时间序列进行平稳化处理。在Eviews中对时间序列GDP进行一阶差分分析并对所得到的数据进行线性分析，得到一阶差分曲线图3：

图3 一阶差分曲线图

由一阶差分曲线图可以看出：预测数列经过一阶差分后的图形显示基本消除了趋势性的影响，趋于平稳化，满足ARIMA模型建模的基本要求。

2． ARIMA模型中p和q的确定及模型的估计。

时间序列预测模块的自相关分析包括对自相关系数和偏相关系数的分析，通过对比分析从而实现对时间序列特性的识别。用Eiews软件对数据进行ADF检验，通过比较可以得出：经过一阶差分后，在95%的置信水平下，时间序列dap通过了ADF检验，Prob.小于0.05达到平稳状态。然后进一步对时间序列进行分析，用Eviews软件绘制一阶差分序列的自相关函数以及偏自相关函数：

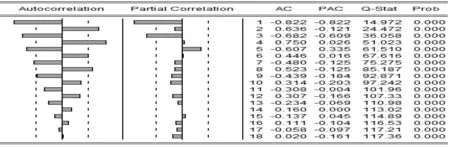
图4 一阶差分序列自相关及偏自相关函数图

由图我们可以看出，它们都是拖尾的，因此可设定为ARMA过程。从它的自相关函数以及偏自相关函数的表可以看出，GDP时间序列的自相关函数在1-6阶都是显著的，并且在6阶以下变化不大，因此可以设定q值为4,5,6；偏自相关函数在3阶以后逐渐减小，且变化不明显，因此先设定p的值为3。于是对于时间序列GDP可以建立三种可能的模型ARIMA (3,4)或ARIMA(3,5)或ARIMA(3,6)模型。

根据变换数列的自相关函数和偏自相关函数的特点，并经过反复测试，通过Eviews软件对模型进行分析，从而确定最终的模型。从Eviews软件得出的三种模型结果对比可以看出ARMA(3,5)模型的参数估计结果(表5)中，AIC与SC值比较小，拟合优度R-squared=0.9908,DW=1.8269,且各系数均通过了显著性检验，因此用ARIMA(3,5)模型来拟合数据。用Eviews软件对ARIMA(3,5)模型进行分析和参数估计，得到模型的回归结果如表3：

表3 ARMA(3,5)模型回归结果

3． 模型的检验和诊断。

为了进一步确定模型的合理性和可靠性，用Rviews软件作出ARIMA模型对该时间序列的残差序列图和自相关函数和偏自相关函数图。

图5 残差序列图

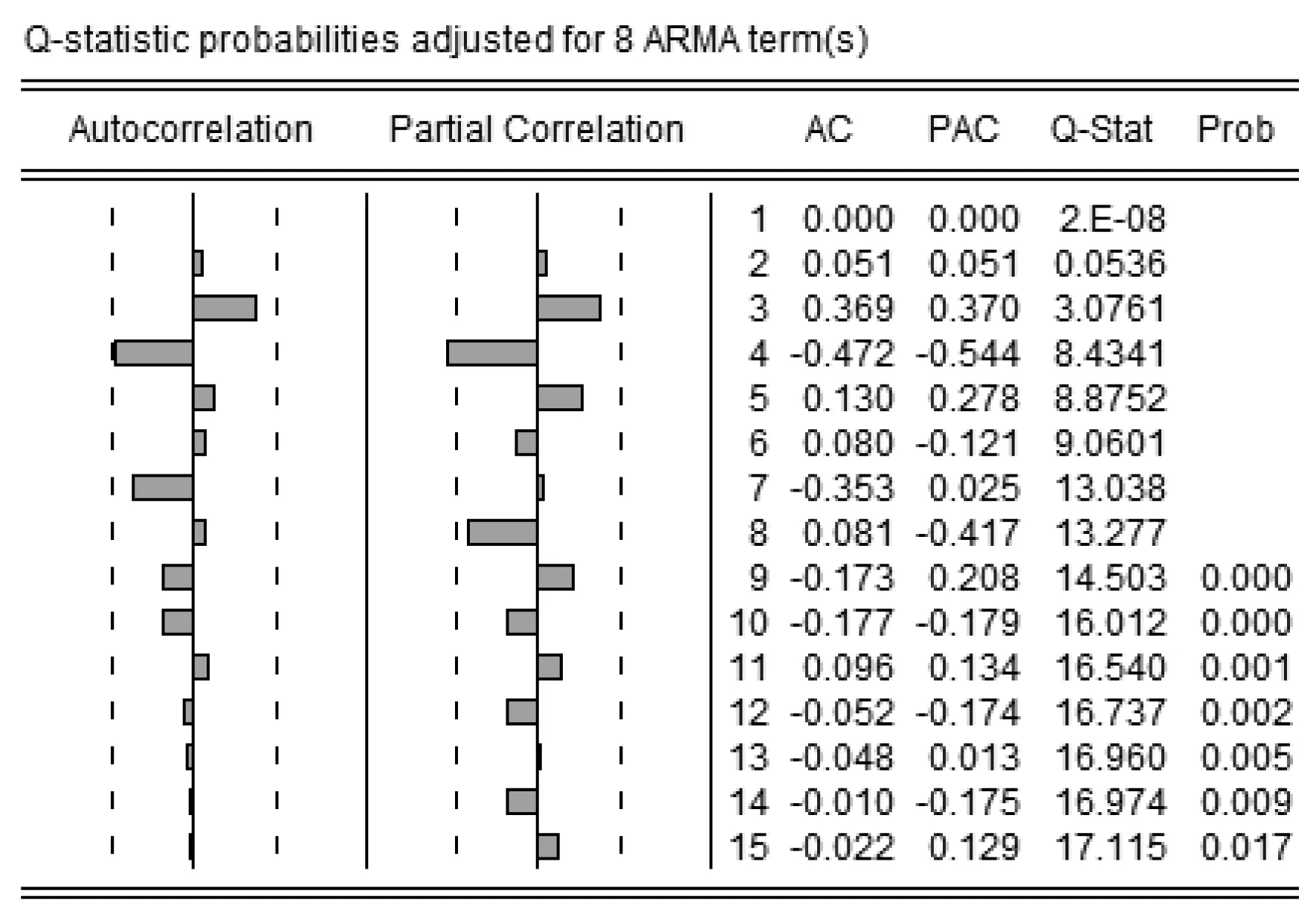
图6 自相关和偏自相关函数图

由残差序列图5可以看出，模型的拟合结果较好，预测值与真实值之间相关指数达到了98%，残差大部分随机分布于置信区间内波动，可得模型效果比较好；在对模型对应残差进行Q统计量检验，得到自相关函数和偏自相关函数图6，从图中可看出残差的自相关函数和偏自相关函数均在置信区间内，且Q-统计量值大于0.05，从而认为残差序列属于白噪声序列，证明所建立模型比较合理，可以用于预测。

4.模型的预测和分析。

在Eviews软件中，我们利用“Dynamic”预测方式对时间序列GDP在2012年的发展趋势进行预测，得到结果如图7。

在图中，实线代表的是时间序列的预测值，两条虚线则提供了2倍标准差的置信区间，由此我们可看出GDP的增长趋势较高。从评价预测的标准可以看到，不相等系数Theil inequality coefficient为0.11，表明模型的预测能力较好；且方差比例较小，说明实际序列的波动较小。用软件单独做出2012年的GDP增长情况，如图8。

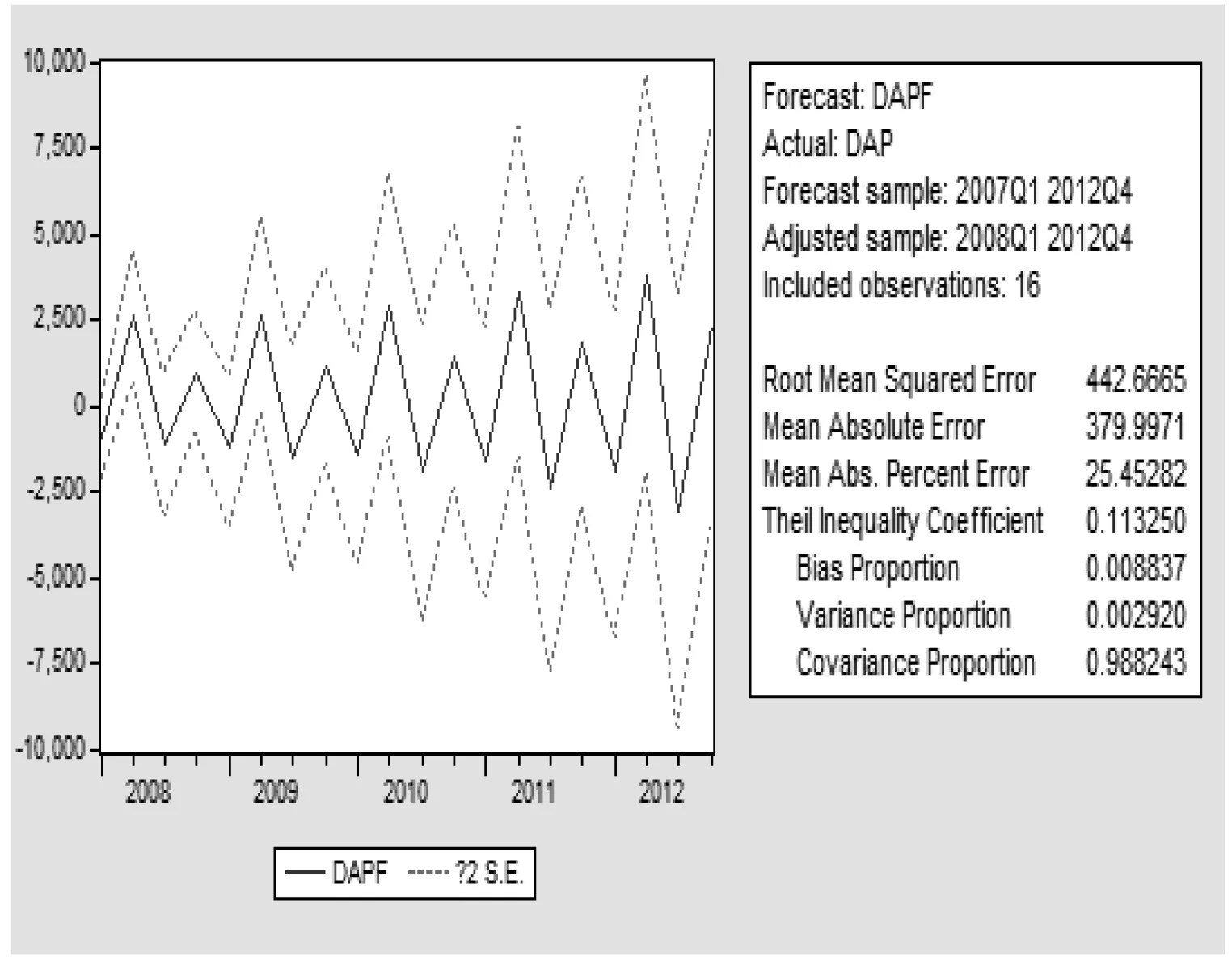
图7 GDP在2012年的发展趋势图

图8 2012年GDP增长情况

从图中可以看出，2012年的GDP增长的趋势远大于降低的趋势，由此可得出结论：2012年山东省总体的GDP将继续增长。

[1]张卫国.以ARIMA模型估计2003年山东GDP增长速度[J].东岳论丛，2004,25(1):79-81.

[2]赵盈.我国GDP时间序列模型的建立与实证分析[J].西安财经学院学报，2006.

[3]王丽娜，肖冬荣.基于ARIMA模型的经济非平稳时间序列的预测分析[J].交通科学与工程，2004,28(1):133-136.

[4]俞天贵，邓文平.基于ARIMA模型的中国煤炭量增长预测[J].统计与决策，2008,24:89-91.

ClassNo.:F222.33DocumentMark：A

(责任编辑：郑英玲)

OntheApplicationofARIMAModelinForecastingRegionalGrowthofGDP

Liu Mingding

(Qindao College，Qingdao Technological University, Qingdao, Shandong 266106，China)

Based on the time series analysis theory, the paper made an analysis of time series of the total value of GDP produced during the year from the first quarter of 2007 to the fourth quarter of 2011 in Shandong Province , and build a time series analysis model to examine the data resulted from the time series analysis . The paper made a prediction of growth trend of GDP in Shandong province in the year of 2012 with the model of time series analysis built.

time series analysis; ARIMA model; GDP; forecasting

刘明鼎，硕士，讲师，青岛理工大学琴岛学院基础部。研究方向：数学模型应用。

1672-6758(2013)07-0068-3

F222.33

A