舰船电缆耦合的有损传输特性分析预测＊

王子磊 聂玉强 阎毓杰

（1.海军驻北京地区舰船设备军事代表室 北京 100176）（2.海军装备部舰船技术保障部 北京 100841）（3.武汉第二船舶设计研究所 武汉 430064）

1 引言

舰船电缆耦合所带来的电磁干扰问题日益突出，在设备或系统因电磁干扰而导致性能降级或功能不正常时，往往要从电缆耦合开始来排查故障原因［1］。电缆耦合［2］已成为工程电磁兼容（electromagnetic compatibility，EMC）中最为迫切需要解决的重要问题之一。

在系统或设备的设计阶段，通过计算提早进行电缆耦合预测，并运用预测结果对电缆的敷设状况、接地、屏蔽等采取相应量化措施，就能够大大减少电磁不兼容的问题。由于电缆耦合的传输线计算通常都是采用无损的理想传输线模型［3］，而实际情况下传输线都是有损的，因此电缆耦合的有损传输特性分析计算成为了开展电缆耦合预测的关键。在此背景下，通过建立相应的电缆耦合等效电路模型，并进行有损传输分析，是实现电缆耦合有损传输特性预测的最佳途径。

本文针对工程中电缆耦合的有损传输问题，着重开展了电缆耦合的有损传输特性分析及预测。主要运用多导体传输线的理论建立电缆耦合的等效电路模型，并分析了有损传输线上的电压电流分分布。在此基础上，仿真分析了电缆耦合的影响因素以及耦合干扰传输特性，从而实现了对电缆耦合的有损传输特性数值预测。

2 电缆耦合的数学建模

对电缆耦合建立多导体传输线的模型需要忽略电缆导体的损耗和周围媒质的损耗［4］，并且假定传播的是横电磁波［5］，即电场、磁场都在与能量传播方向相垂直的横截面上［6］。

2.1 耦合计算模型

在实际工程应用中大量碰到的是多芯电缆或是多根电缆所构成的传输线系统，为此有必要将两电缆耦合的分析方法推广到对n个电缆耦合情况的分析。考虑由n根导线组成的n＋1根导线系统（其中一根为参考导线），单位长度的分布参数矩阵可表示为

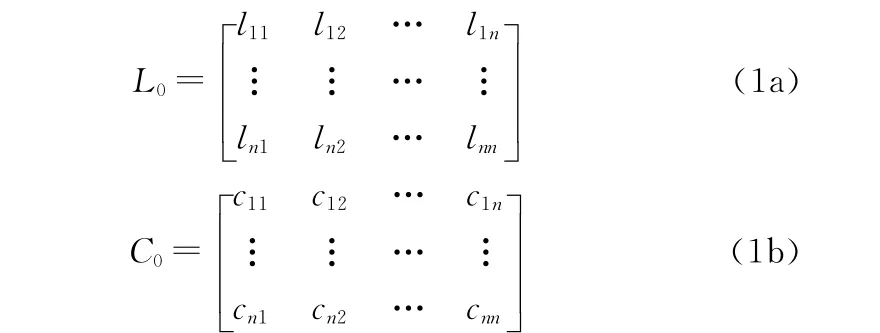
L0、C0是对称、对角占优的正定矩阵。其中，矩阵里元素下标ii代表了自电感或自电容，下标ij则代表了互电感或互电容。按照三导体传输线［7］的分析方式，得到多导体传输线上电压和电流的正弦稳态解如下：

由上式可确定受扰导线上耦合到的电压和电流值。其中，β为相位常数，Λ为n阶单位对角矩阵。

2.2 有损传输特性分析

均匀传输线的原始参数可用每单位长度的线路参数来表示［8～9］。均匀传输线上连续分布的电阻R0和电感L0分别引起相应的电位降致使线间电压沿线变化；均匀传输线导线间连续分布的漏电导G0和电容C0分别在线间引起相应的泄漏电流和位移电流，致使电流沿线变化。在相当宽的频率范围内四个参数内都是恒定的，即可认为它们均为常量。

图1为二线均匀传输线的集中参数电路，选择传输线始端（激励源端）作为计算距离的起点。x轴的正方向由始端指向终端。传输线上的电压u及电流i的参考方向如图1所示。

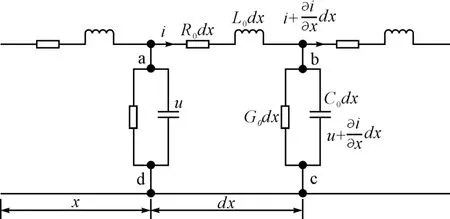
图1 有损均匀传输线的集总参数电路

对结点b列写KCL方程，对回路abcda列写KVL方程，约去dx并略去二阶无穷小量，得到一组偏微分方程：

由于传输线方程是偏微分双曲型方程组，在给定的初始条件边界条件下，可以唯一地确定u（x，t）和i（x，t）。若始端电源为角频率ω的正弦时间函数。在电路达到稳态的情况下，沿线的电压和电流是同一频率的正弦时间函数［10］，用相量法［11］求解可得有损传输线的正弦稳态解为

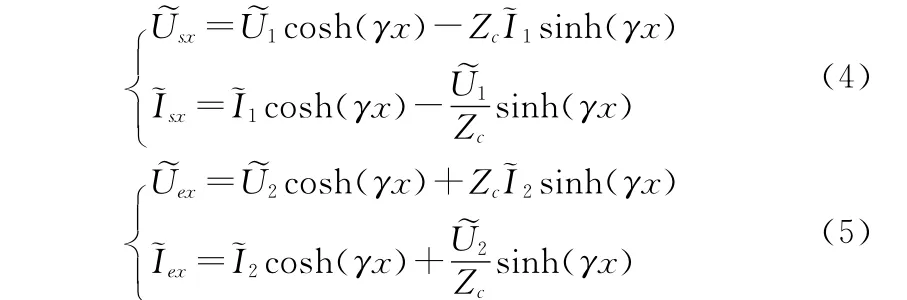
3 仿真

仿真系统由三条信号电缆和一条地线构成：用G表示产生干扰的电缆（干扰电源电压为1V，频率1MHz），用R1、R2表示被干扰的两条电缆。它们的长度均为300m，并排放置在距地高度h为200mm的地方。每条电缆的截面半径为10mm，其中导线表皮绝缘层（εr＝3.6）的厚度为4mm，电缆G与R1的间距为100mm，电缆G与R2的间距为200mm。

仿真不同频率下R1，G的耦合系数以及R2，G的耦合系数的情况，如图2所示。

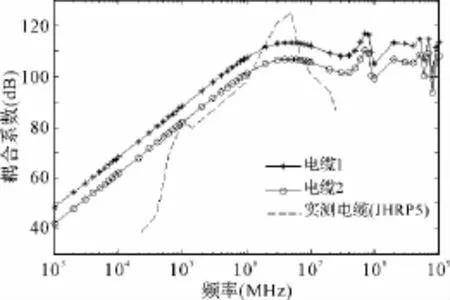
图2 电缆耦合系数的频率响应

如图2，在“电大”情况下高频耦合响应受到分布参数效应的影响，从而形成多个模式驻波所构成的震荡。图2中的第三条虚线是根据某工程电缆分类敷设试验的实测数据描点得到的，可以看到，它与预测结果曲线的趋势基本吻合。

接下来，针对首先电缆的有损传输特性，设置受扰电缆线路原参数R0＝0.06Ω／m，L0＝1.40×10－3H／m，G0＝3.75×10－8S／m，C0＝9.0×10－9F／m。终端为一480Ω的电阻负载，始端的电压为220V。通过搭建仿真电路，仿真得到负载电压的幅频特性曲线如图3，当电源的频率在45Hz～55Hz变化时，负载电压幅值在215.1°～216.6°变化；当电源的频率为50Hz时，负载电压是215.8V。图4仿真了受扰电缆的始端电压和终端电压的相位差，图中V（R1：1）是负载电压，V（V1：＋）是电源电压，可见负载电压滞后于电源电压，其滞后角度可根据时间差计算得到。

图3 负载电压的幅频特性曲线

进一步考察受扰电缆上有损传输的电压幅频特性。仿真计算传输线路中点与负载端的电压幅频特性，如图5所示。可以看到传输线中点处上电压幅频曲线与负载端的电压幅频曲线变化趋势一致，只是电压幅值要高一些，这也正好反映了有损均匀传输线的传输特性。

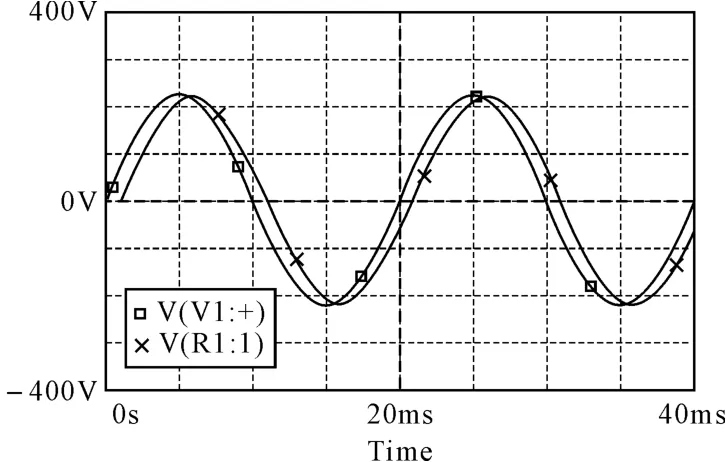
图4 始末端电压正弦稳态波形

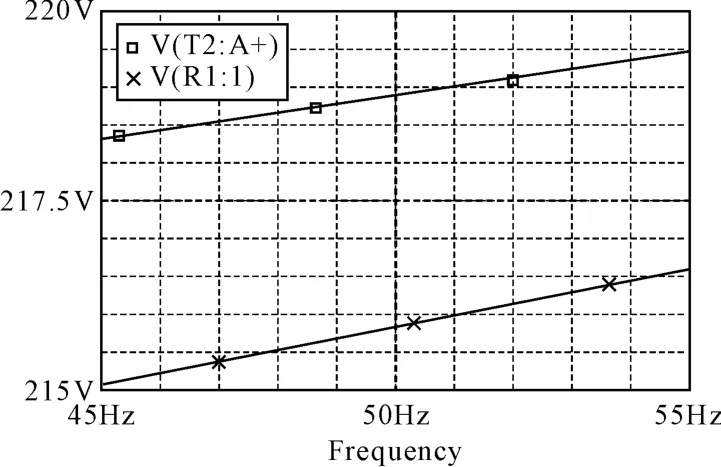
图5 传输线中点与负载电压的幅频特性曲线对比

4 结语

本文针对工程中的电缆耦合的有损传输问题，着重开展了电缆耦合的有损传输特性分析及预测。主要运用多导体传输线的理论建立电缆耦合的等效电路模型，并分析了有损传输线上的电压电流分分布。在此基础上，仿真分析了电缆耦合的影响因素以及耦合干扰传输特性，从而实现了对电缆耦合的有损传输特性的数值预测。

［1］毕季明，黄小华.海军舰船电磁兼容控制技术与措施［J］.舰船电子工程，2007，27（2）：201－203.

［2］Levin B.M.Calculation of Crosstalks in Multiple－Conductor Cables［C］／／Proceeding of DIPED'07，2007：211－214.

［3］Paul C.R.Analysis of Multiconductor Transmission Lines［M］.New York：John Wiley Interscience，1994.

［4］Vance E F.Coupling to shielded cables［M］.New York：John Wiley ＆Sons Press，1978.

［5］Clayton R.Paul.Solution of the Transmission－Line Equations Under the Weak－Coupling Assumption［J］.IEEE Transactions on Electromagnetic Compatibility，2002，44（3）：413－423.

［6］Michel A，Mircea I，Lin C C.Transient electromagnetic field coupling to long shielded cables［J］.IEEE Trans.on Electromagnetic Compatibility，1980，22（4）：276－282.

［7］Feliziani M，Maradei F.Full－wave analysis of shielded cable configurations by the FDTD method［J］.IEEE Trans.On Magn.，2002，38（2）：761－764.

［8］Pignari S，Canavero F.G.A Transmission Line Simulator for EMC in Complex Electronic Systems［J］.International Journal of Numerical Modelling：Electronic Networks，Devices and Fields，1997，10：13－34.

［9］Clayton R.Paul.Computation of Crosstalk in a Multiconductor Transmission Line［J］.IEEE Transactions on Electromagnetic Compatibility，1981，23（4）：352－358.

［10］Savage J.S.，Smith W.T.Capacitance Calculations for Cable Harnesses using the Method of Moments［J］.IEEE Transactions on Electromagnetic Compatibility，1995，37（1）：131－137.

［11］Gavrilakis A.，Al－Asadi M.M.，Duffy A.P.，et al.Method for Prediction of Capacitance of Shielded Transmission Lines［J］.IEEE Electronics Letters，2001，37（23）：1424－1425.