价格收敛于价值吗——对价值规律作用形式的证明
2013-11-27朱殊洋中共广州市委党校经济学教研部广东广州510070
□ 朱殊洋(中共广州市委党校 经济学教研部,广东 广州510070)
价值规律作为经济系统的基本规律,其作用形式如何?马克思对于价值规律的作用形式给出了简要的描述:“一般说来,一切商品的价值,只是由于不断变化的市场价格趋于平衡才能实现,而这种趋于平衡又是供给和需求不断变化的结果。”[1]
对于上述观点,马克思只进行了描述性的分析,而没有给出严格的证明。因此,学术界对于价值规律的作用形式,出现了两种不同的观点。一种观点认为,价值规律作用形式是价格围绕价值变动,但是价格并不收敛于价值;另一种观点认为,价格围绕价值变动,而且价格收敛于价值。两种观点都是基于马克思的论断而提出的。但无论哪一种观点,都没有对价值与价格的动态关系给予严格的数理描述和证明。本文尝试运用规范的数理分析方法,对价格动态趋势进行考察。
一、符号与假设
符号设定上,本文模型用D表示价格,d表示需求,s表示供给,D0表示均衡价格即价值。分析假设上,为了分析价格的收敛性,我们首先需要指出价格函数的性质。首先,价格函数是短期价格函数累加,考虑长期函数是一种质点分析,故而每个短期函数之间存在过渡函数,也就是长期函数是连续的,这样根据文献[2],长期价格函数可以表示为初等函数。其次,马克思将长期价格定义为供求差额的函数,即D=D(d-s),且它是这一差额的增函数[3]。于是做一个坐标系,纵轴为长期价格,横轴为供给和需求。如果供给不变,则得到长期价格对需求的变化曲线,这一曲线向右上方倾斜;如果需求不变,则得到长期价格对供给的变化曲线,这一曲线向左下方倾斜。两条曲线的交点为均衡点,在这一点,供求相等,且长期价格不受供求影响。现在的问题是,马克思长期价格曲线收敛于均衡点吗?答案是肯定的。为了证明这一结论,我们需要给出一个引理。
二、长期价格函数的一个形式
引理:马克思长期价格函数可以表示为ΔD=k(d-s),其中k为常数。
证明:对长期价格函数,我们假定该函数可微,这样就可以借助于微元法将曲线近似化为直线从而导出结果。分为两种情况,第一种初始点为均衡点,第二种初始点不在均衡点。
第一种情况:初始点在均衡点的情况。虽然这是一种特殊情况,但是却是证明一般情况的基础,也就是说,为了证明一般情况总是要设法将一般情况转化为特殊情况。这就是我们证明的基本思路。
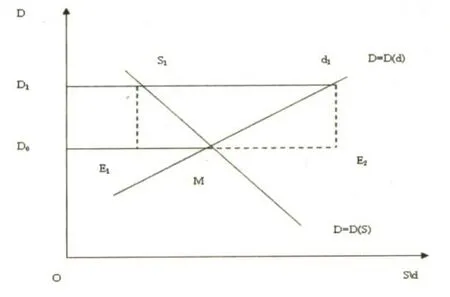
图1 初始点为均衡点下D的变动
首先作图1,即与S、d的关系图。图1中,D=D(S)为D随S变化的长期曲线,D=D(d)为D随d变化的长期曲线,相交处为均衡点M。M点的横坐标D0为长期价格均衡点,M点的纵坐标是供求均衡S0=d0点。设t0在时刻供求开始变化,因而长期价格也发生了变化,由原来的D0上移到D1。令D1-D0=ΔD。D=D1与S、d曲线的交点分别是 S1、d1。过点S1、d1分别作垂直于D=D0的直线,交D=D0及其延长线 E1、E2两点,则S1E1=d1E2=ΔD
由图1可知
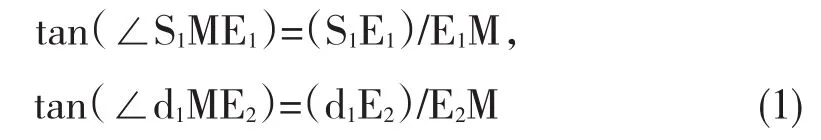
因为两个角不变,所以其正切为常数,令tan(∠S1ME1)=λ1,tan(∠S2ME2)=λ2,将其代入(1)得
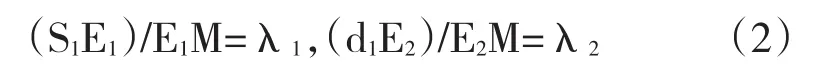
即
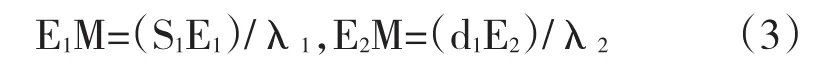
上两式两边相加得
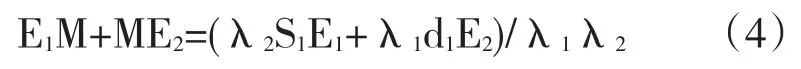
因为E1M+ME2=d-S,S1E1=d1E2=ΔD,所以上式为
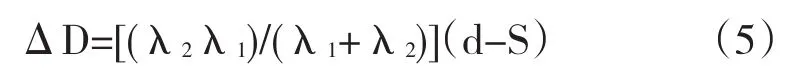
取 k=(λ2λ1)/(λ1+λ2),则得到ΔD=k(d-S)。这就是第一种情况下长期价格随供求变化的规律。
考察第二种情况:初始点不在均衡点的一般情况。作图2。图2中,假设初始点位于均衡点之上的D1处,从某一时点开始因为供求变化,价格D1向上移动到D2的位置,这一位置高于均衡点。设 D=D1与 D=D(S)、D=D(d)曲线分别交于S1、d1,D=D2与S、d曲线分别交于S2、d2,均衡价格为 D0。令 D1-D0=ΔD1,D2-D1=ΔD2。过S1点作垂直于D=D1的直线,分别交D=D2、D=D0于 F1、E1;过 d1点作垂直于 D=D1的直线,分别交 D=D2、D=D0延长线于F2、E2。
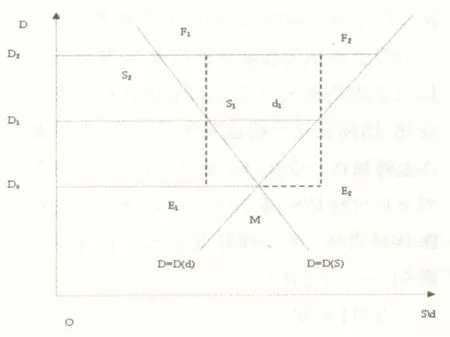
图2 初始点不是均衡点下D的变动
根据平行线比例线段定理,得
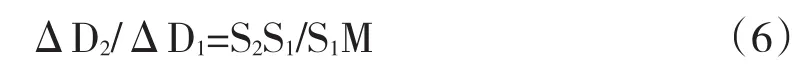
又因为三线平行,即D=D0PD=D1PD=D2,所以Δ d2MS2∽Δd1MS1,因此有
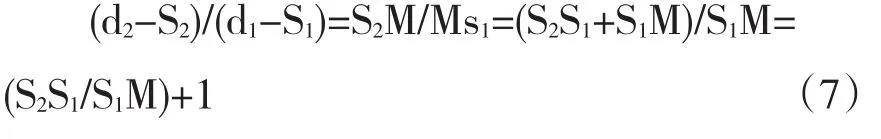
结合(6)、(7)得
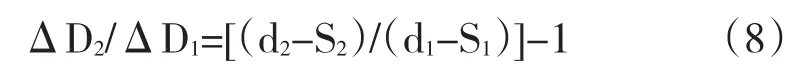
由上式得
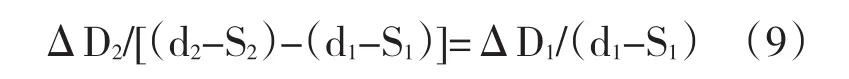
由第一种情况的证明可知,ΔD1/(d1-S1)=λ,所以
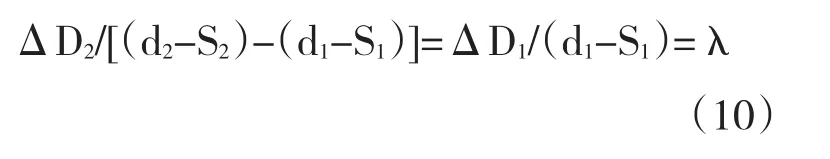
由此得
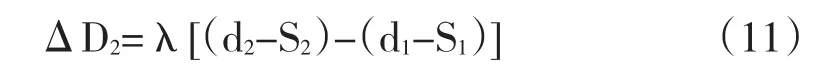
又因为ΔS2F1S1∽ΔME1S1,Δd2F2d1∽ΔME2d1,所以
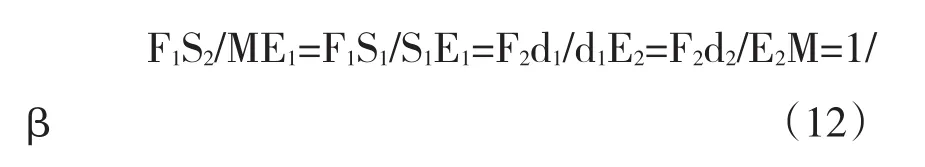
其中β为比例常数。由(12)得
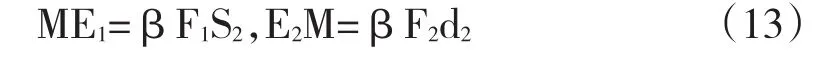
上两式两边相加得
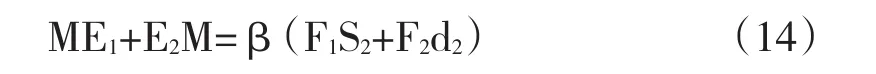
由图2可知
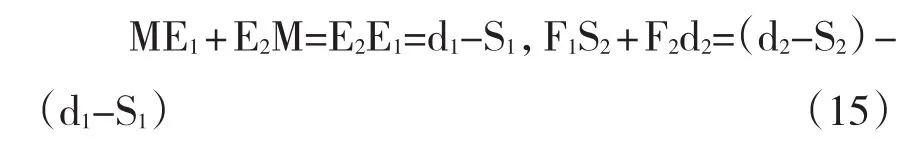
将(15)代入(14)得
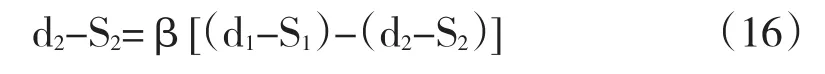
即
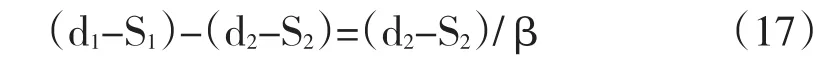
将上式代入(11)得
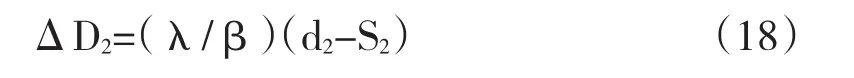
取k=λ/β,则得到ΔD2=k(d2-S2)。
结合两种情况得到长期价格函数的微元形式ΔD=k(d-S)。证毕。
三、收敛性分析
定理:长期价格函数是大范围稳定的。在其均衡点处供求相等,因而长期均衡价格不受需求的影响。也就是说,价格围绕价值变动且最终收敛于价值。
证明:做李雅普诺夫能量函数

其中ρ为大于零的常数,供给S也是常数。由(19)可见能量函数大于等于零,因而只在零点处平衡。对能量函数(19)求时间的导数得
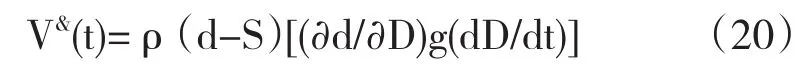
由引理的结果ΔD=k(d-S)代入上式得

由引理∂d/∂D<0知,所以有
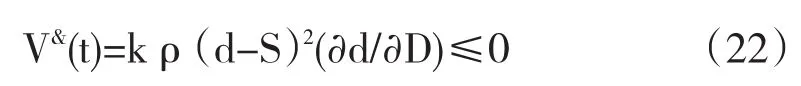
对于(22),只有当d-S=0时,V&(t)=0,否则均有V&(t)<0。这意味着,尽管价格不在均衡点,但是由于能量函数会逐渐变小进而趋于零,从而导致价格一定会大范围收敛于均衡点,且在均衡点处供求是相等的,因此在均衡点处价格不受需求的影响。证毕。
做图3以便形象地说明收敛过程。设D的初始点位于D1的位置,这时有d1<S1,由此导致生产者减少产量,需求者扩大需求,于是D曲线上移至D2,这时 d2>S2,于是又出现生产者增加产量、需求者减少需求的调整,于是价格下移。如此下去最终D曲线趋于D0。D=D0就是长期价格均衡轨线,在D0点处,d=S。
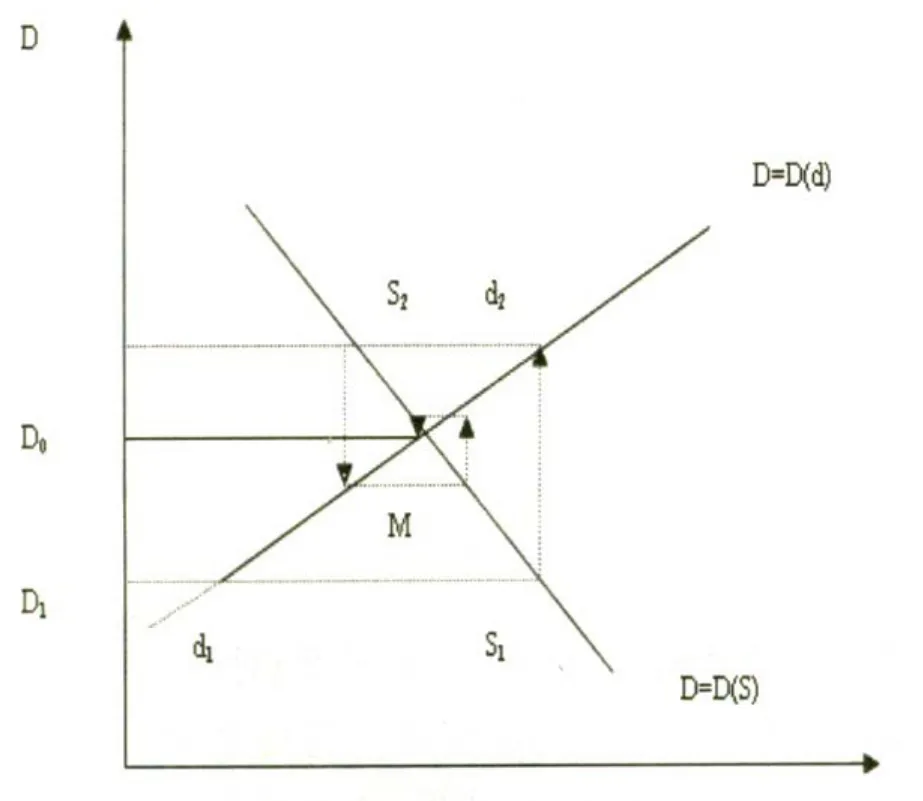
图3 长期D曲线的收敛
四、小结
本文通过规范的数理分析和证明,尽管价格与价值的瞬时相等是偶然的,而且价格总是围绕价值进行波动,但是从长期看,这一波动是收敛的,即价格围绕价值变动,而且从长期看价格收敛于价值。因此,价格围绕价值变动且收敛于价值恰恰是价值规律作用的表现形式。本文模型为马克思关于价值规律作用形式的观点提供了一个数理阐释。
[注 释]
[1]马克思恩格斯全集,第16卷(中译本)[M].北京:人民出版社,1964.162.
[2]龙洪波、伍毅.用初等函数表示一类分段函数的方法[J].数学通讯,1994,(11).12—14.
[3]马克思.资本论,第三卷(中译本)[M].北京:人民出版社,2008.211.
[1]朱殊洋.单位商品价值量与劳动生产率的关系[J].马克思主义研究,2011,(5).
[2]朱殊洋.社会必要劳动时间是怎样形成的[J].海派经济学,2011,(2).
[3]郑志国.劳动力价值新探[J].岭南学刊,1995,(3).
