基于免疫粒子群算法的闭塞分区划分优化设计

康 宁，陈永刚，林俊亭，曹 岩

(1.兰州交通大学自动化与电气工程学院，兰州 730070;2.兰州交通大学电子与信息工程学院，兰州 730070)

目前，我国铁路线路里程正在不断的增加，同时要保证在自动闭塞制式下，不同列车在通过相隔数个闭塞分区时，能实现同一区间内的安全追踪运行。列车相隔分区数目越少，追踪间隔时间则越短。而根据列车扣除系数经验公式，追踪间隔时间越短，列车通过能力就越大［1］。因此，为了保证行车安全，提高列车运输能力，需要对闭塞分区划分问题进行进一步的优化。

近年来，在闭塞分区划分问题研究方面，有关学者都取得了一定的成果。国外学者曾使用梯度搜索算法［3］、DE(differential evolution)算法［4］、遗传算法［5］、最大-最小蚁群算法［6］等人工智能算法针对城市轨道交通系统进行了闭塞分区的划分研究;而在国内方面，2011年刘剑锋等人对准移动闭塞方式下列控系统为CTCS2级的铁路区间通过信号机布置设计了启发式仿真算法［7］;卫和君通过对人控驾驶模式下列车追踪间隔时间的计算方法，实现了对客运专线CTCS-3级列控系统的闭塞分区划分［8］。但这些研究都很少将优化算法应用于干线铁路自动闭塞分区划分中，干线铁路所要考虑的约束条件更多且更为复杂。而免疫粒子群算法通过按比例复制高亲和度抗体，添加变异算子，为新个体产生提供途径，增加了种群多样性，可实现闭塞分区快速、准确划分。

1 闭塞分区划分模型

1.1 模型定义

如图1所示，设两站间信号机的架数Nsignal，每架信号机的位置为 xi(i=1，2，…，Nsignal);x0、xNsignal+1分别为两车站间出站信号机、进站信号机的位置坐标，则计算闭塞分区长度是

图1 变量定义描述

1.2 目标函数

闭塞分区划分问题是在保证行车安全及具体施工要求的约束条件下，找出划分节点，求得最短追踪间隔。它是一个复杂的多目标多约束问题，为此，本文建立两种策略下的划分模型。

“效率”策略是指在列车制动距离和闭塞分区有效长度满足的情况下，通过最小化追踪列车间隔时间得到最大的列车通过能力，进而提高自动闭塞区段上的列车运行数目。其目标函数为

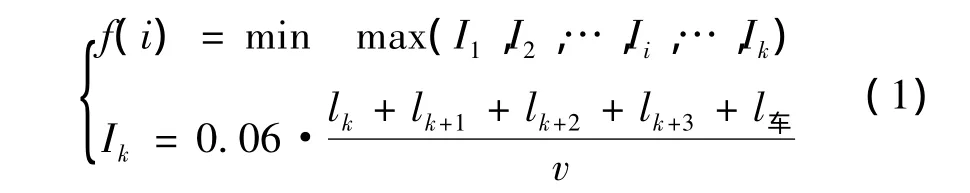
其中，Ik为列车追踪间隔，在四显示自动闭塞制式下前后行列车应间隔4个闭塞分区追踪运行;v为列车运行的速度;i为在闭塞分区范围内划分节点数目，i=1…n;max(I1，I2，…，Ii，…，Ik)为由出站信号机经 k+2架通过信号机至进站信号机最长追踪间隔。

“经济”策略是指在列车追踪间隔时间确定的前提下，最小化信号机的数目。其目标函数为

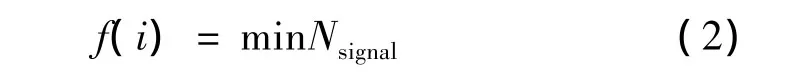
其中，Nsignal表示两站间信号机的架数即划分。

1.3 约束条件

闭塞分区实际划分时要考虑多个约束条件，如式(3)所示，包括列车紧急制动距离、轨道电路长度、区间最小分区数目等，其中lmin为工程人员由现场实际情况确定的闭塞分区的最短长度，lcircuit为轨道电路极限长度，划分节点数n=N+1，H为预先设定追踪间隔时间。制动距离Sb和附加距离S附长度之和为闭塞分区长度 li，max Sb(vi，vi+1，ij)为列车自坡道值 ij处从高速度等级vi+1降至相邻低速度等级vi的最大制动距离。

1.4 适应度函数

构造适应度时引入罚函数法，将一个足够反映约束条件的惩罚项包含到适应度函数中，对复杂的约束优化问题进行无约束处理，通过惩罚因子大小的选取调节适应度函数的惩罚力度，从而影响算法的收敛速度。

效率策略下适应度函数为

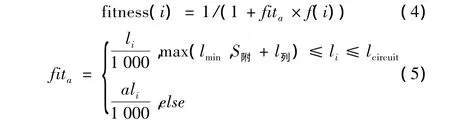
在式(4)和(5)中，a为惩罚因子，取值范围为10～20。公式(5)说明闭塞分区长度不满足实际轨道电路极限长度和紧急制动距离时，适应度值减小。

经济策略下的适应度函数为

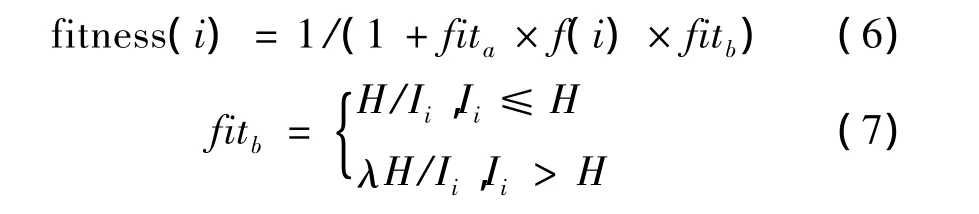
在式(6)和(7)中，λ为惩罚因子，取值范围为10～20。公式(7)说明追踪间隔大于给定追踪间隔时，适应度函数值减小。

2 免疫粒子群算法优化过程

2.1 免疫粒子群算法总流程图

IA－PSO算法可分为两部分，如图2所示，一为基本PSO算法，用于控制基本的优化迭代过程。当算法在运行过程中，某一粒子发现最优解，其余粒子就会聚集，种群多样性降低，如果发现其为局部最优解，粒子群无法再在解空间继续搜索，陷入早熟收敛。二为引入人工免疫机理，经过克隆复制，柯西变异，克隆选择算子，加大种群多样性，增强全局搜索能力。

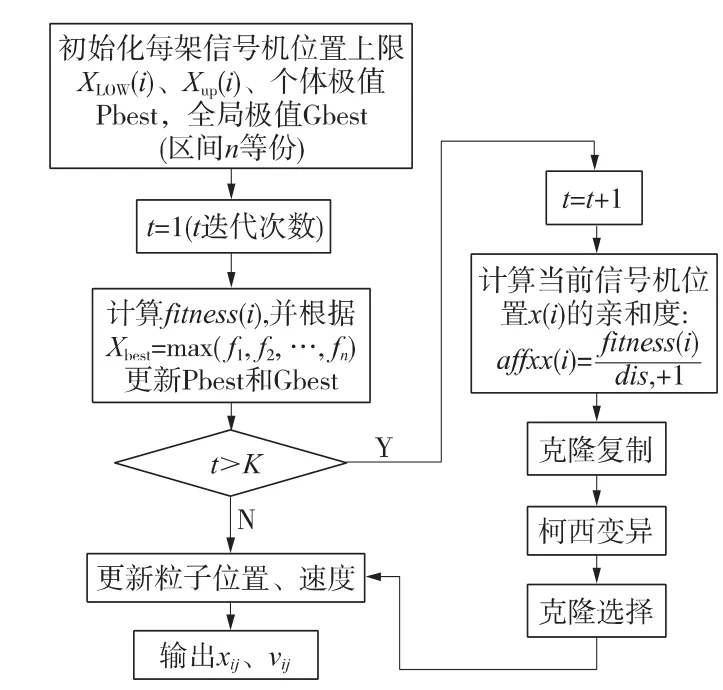
图2 免疫粒子群算法流程

2.2 算法设计

Step1 根据式(2)确定种群数目，即信号机数目n，将区间n等份，线路上第i架信号机位置取值下限:XLow(i)=X(i)－300，取值上限:Xup(i)=X(i)+300，个体极值 Pbest，全局极值 Gbest，维度范围 j∈(1，p)。

Step2 根据约束条件对划分结果影响设计的不同策略下的适应度函数式(3)、(4)、(5)、(6)，求解各粒子适应度值;由极值更新策略Xbest=max(f(1)，f(2)，…，f(n))得到个体极值 Pbest、全局极值 Gbest。

Step3 根据t值是否超过设定阈值K判断是否陷入局部最优解，若Gbest没有更新，累加全局最优解迭代次数t=t+1，t未达到给定阈值K，转向step4，否则，t清零。

Step4 将粒子看做抗体，计算亲和度

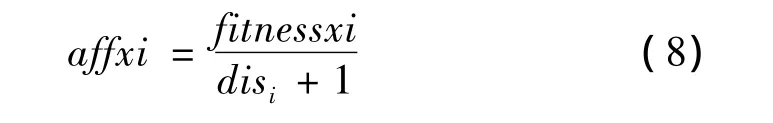
其中，disi为第i个粒子与全局最优粒子gbest在第j维度上的距离，即待优化长度与全局极值的距离。

Step5 第i个粒子被克隆复制的数目

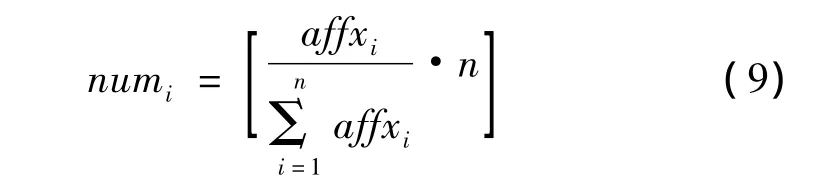
通过抗体抑制原理，亲和度值越小，被克隆数目越少，基因优良性越保持。

Step6 进行柯西变异，对于每个克隆个体，根据父代个体亲和度变化采用变异操作。柯西变异的范围随着t值的减小而缩小，当t值确定，父代种群的亲和度连续δ代不发生变化时，选取t(k+1)=0.8*t(k)，为抗体x的父代变异体，参数η控制柯西随机变量ijcauchy(t)的衰减。

Step7 进行克隆选择，采用轮盘赌(Roulette wheel)方法将父代适应度函数进行排序，从父代个体中选出适应度最高的粒子作为下一代个体，淘汰适应度较低个体。

Step8 对粒子位置坐标xij和速度vij(即追踪间隔时间)进行更新。其中，学习因子c1、c2为固定值，r1，r2∈[0，1]，Pij为当前信号机位置坐标最优解，Pgj信号机位置坐标经亲和度值升序排列后选出的最优位置。

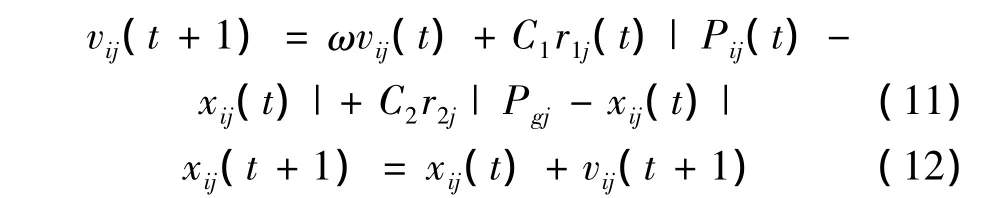
Step9 若满足迭代次数，算法停止，输出xij，vij值，否则转向step2。

3 闭塞分区划分检验

闭塞分区划分检验分为列车追踪间隔检验、列车起动检验，列车停车检验，特殊线路条件检查。主要通过对信号机位置调整，使信号机间的列车追踪间隔小于给定的间隔时间，并通过对速度参数控制，不断计算列车牵引和制动性能并设定制动触发点，根据动能公式、动量定理，牵引时保证列车能够在坡段起动需使列车起动牵引力满足:Fq≥ [Gq(+iq)+P(+iq)]g×103;制动时，在列车达到最大速度前提下，制动距离在闭塞分区划分的范围内，满足:L闭≥(Sb+la)/(M－2)，并考虑特殊线路的限制因素，如坡道、曲线半径等，检验模型如图3所示。

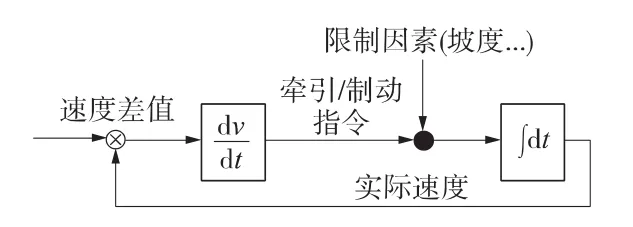
图3 划分检验模型

4 案例分析

选取A站—B站为待布置通过信号机的区间，A站出站信号机位置为270.746 km，B站进站信号机位置为284.026 km，则区间全长13.28 km，设列车在区间平均运行速度为100 km/h，列车长度为800 m，按四显示自动闭塞布置，设闭塞分区最小长度为1 000 m，最大闭塞分区长度为1 400 m，初始种群20个，优化10次，每次最大迭代次数250次，取最优的优化结果输出。图4所示为两种策略下，算法的各代群体平均适应度与最大适应度的变化趋势。

从图4中可以看出，随着迭代次数的增加，群体的平均适应度和最优适应度波动减小，表明算法可以维持种群的多样性，避免早熟收敛发生。在效率策略和经济策略下，算法运行到接近200代群体的平均适应度和最优适应度的减小趋势已较为缓慢，可将算法250代时的计算结果作为最终的布局方案。运行结果见表1，经济策略下追踪间隔为min max(I1，I2，…，Ik)=3.96 min，效率策略下追踪间隔为3.25 min，预先设定的列车追踪间隔为5 min，并且经检验所有信号机满足制动距离要求，说明算法是有效的。

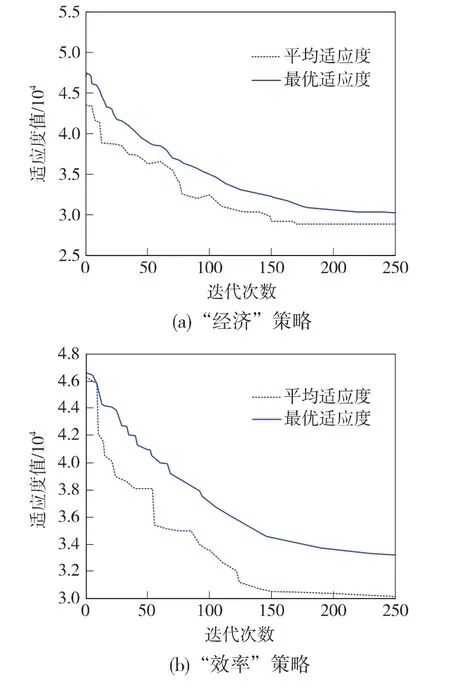
图4 群体适应度变化曲线

表1 基于免疫粒子群算法的优化结果

评价算法性能时，Ef为波动率，反映了初始条件下逼近最优解的程度，如图5所示，其值越小，说明算法的鲁棒性越好。

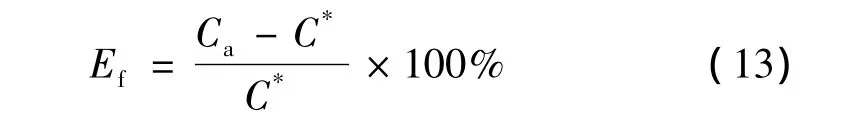
式中，C*为问题的期望最优值;Ca为算法多次运行所得的平均值。

图5 波动率曲线

Ef1、Ef2分别为“经济”和“效率”下的波动率。试验结果表明，IM-PSO法运行到250次得到最优解，波动率小，算法鲁棒性好。

5 结语

使用免疫粒子群算法对信号机的数目和位置进行初始化，并对种群进行克隆、变异、选择等操作，完成列车追踪间隔检验和列车起停车检验，实现闭塞分区的快速、准确划分。最后通过实际案例，考虑“经济”、“效率”等因素对该算法进行验证，结果表明该算法确实能改善闭塞分区的优化划分。

［1］董昱.区间信号与列车运行控制系统［M］.中国铁道出版社，2008.

［2］Gill D C，Goodman C J.Computer-based optimization techniques for mass transit railway signaling design［J］.IEE Proc-B，1992，139(3):261-275.

［3］Chang CS，Du D.Improved optimization method using genetic algorithms for mass transit signaling block-layout design［J］.IEE Proc-Electr.Power Appl.，1998，145(3):266-272.

［4］Ke B.R，Chen M C，Lin C L.Block-layout design using MAX-MIN ant system for saving energy on mass rapid transit systems［J］.IEEE Transactions on Intelligent Transportation System，2009，10(2):226-235.

［5］卫和君.客运专线CTCS-3级列控系统牵引计算与闭塞分区划分技术［J］.铁路技术创新，2010(5):24-28.

［6］于宗艳，韩连涛.免疫粒子群优化算法及应用［J］.计算机仿真，2008(12):208-211.

［7］雷德明，严新平.多目标智能优化算法及其应用［M］.北京:科学出版社，2009.

［8］刘澜，杜文.多信息自动闭塞列车速度——间隔控制模型及算法［J］.铁道学报，2000(6):8-12.

［9］毛保华.列车运行计算与设计［M］.北京:人民交通出版社，2008.

［10］卫和君.铁路自动闭塞分区划分技术展望［J］.长沙铁道学院学报，2003，21(4):99-102.

［11］薛长虹.青藏铁路关角特长隧道内自动闭塞设计探讨［J］.铁道标准设计，2012(4):127-130.

［12］傅世善.自动闭塞设计的新理念［J］.铁道通信信号，2004，40(5):16-18.