改进的多进制LDPC码的EBF算法

佟宁宁，赵旦峰，吴宇平

1)哈尔滨工程大学信息与通信工程学院，哈尔滨150001;2)黑龙江工程学院电气与信息工程学院，哈尔滨150050

低密度奇偶校验码 (low-density parity-check codes，LDPC)码与Turbo码［1］是迄今为止纠错性能最好的信道编码技术.多进制LDPC码具有高可靠性、快速收敛性及较强抗突发错误能力［2-7］，并可提高通信系统的有效性［8-14］，因此成为近年的研究热点.LDPC码的校验矩阵构造方法可以分为结构构造方法［15-20］和随机构造方法.结构构造的LDPC码的优势在于它具有低复杂度的编译码器结构，从而可降低编译码器的硬件实现复杂度，但选择码长和码率等参数不够灵活，兼容性较差.而在码长趋于无穷时，随机构造的LDPC码与结构构造的LDPC码相比更接近Shannon限，码长、码率等参数选择灵活，但其优越性能是以高编译码复杂度为代价的，阻碍了其实际应用.因此，降低随机构造多进制LDPC码的编码复杂度，使其进一步实用化具有重大意义.本研究针对随机构造多进制LDPC码编码复杂度高的缺陷，基于具有线性编码复杂度的多进制LDPC码迭代编码方法，提出一种改进多进制LDPC码随机构造算法——改进的扩展比特填充(extended bit-filling，EBF)构造算法.与原EBF算法相比，本研究提出的算法可在不损失编码增益的情况下，降低系统的编码复杂度.

1 多进制LDPC码的迭代编码算法

王鹏［21］提出的基于二元LDPC码的迭代编码算法，很容易被转变成适用于多进制的LDPC编码方法.若多进制LDPC码的校验矩阵具有如图1的下三角结构，其中对角线的位置上全为有限域GF(q)上的非0元素，而其余的非0元素均在对角线的左边，则可直接采用迭代编码算法进行编码.设码字符号向量为c∈Fn，将其分为信息位符号向量s∈Fn－m和校验位符号向量p∈Fm两部分，即c∈(s，p)，则该编码算法为

其中，l∈［0，n － k －1］;Hi，j表示校验矩阵H的第i行，第j列上的元素，且k=n－m.由式(1)可见，该编码过程就是利用校验矩阵H各行的约束关系，采用后向迭代的方法，依次计算每个校验位符号值.

图1 具有下三角结构的校验矩阵Fig.1 The parity check matrix with lower triangle structure

多进制迭代编码方法与二进制迭代编码方法的原理基本相同，区别在于:在二进制迭代编码运算过程中，采用的是二进制的与以及异或运算，而用多进制迭代编码方法运算时，采用的是GF(q)域上的乘加运算;多进制迭代编码运算过程中引入了GF(q)域上除法运算，与二进制迭代编码算法相比，增加了编码复杂度.为简化运算量，可令对角线上的元素全为1，此时，式 (1)可写为

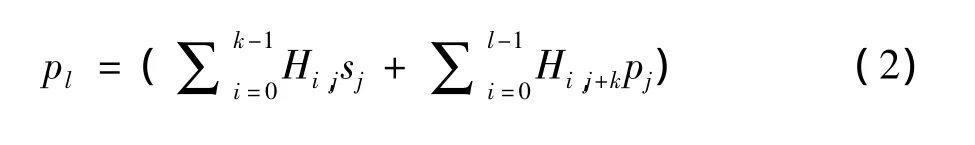
2 改进的扩展比特填充构造算法

针对随机构造多进制LDPC码的高编码复杂度，基于线性编码复杂度的迭代编码算法，本研究提出一种直接构造具有下三角结构的非规则多进制LDPC码的方法——改进的多进制EBF算法，从改进编码方案和构造校验矩阵方面降低算法复杂度.

EBF算法的基本原理，是在保持给定的girth约束条件下，将GF(q)域上的非0元素依次填充到校验矩阵 H中［22］.在整个算法的执行过程中，girth约束一直都是变化的.在算法最初执行时保持girth约束的最大值g，直到不降低girth约束就不能给校验矩阵中填充非0元素时为止.这时girth约束可降低 (以2递减)，算法在保证新的girth约束条件下继续.如此循环，当所有的非0元素都成功填充到校验矩阵中，或girth约束低于给定的最小值g时，算法停止.本研究提出的改进多进制LDPC码的EBF算法与无改进的EBF算法流程基本相同，改进点包括:

改进1 按列号由大到小依次排序，将GF(q)域上的非0元素添加到校验矩阵H的每一列.

校验矩阵的环分布是决定LDPC码纠错性能好坏的关键，因此构造校验矩阵H时，如何消除短环(4环和6环)就显得十分重要［23］.由于EBF是随机构造方法，每次填充GF(q)域上非0元素时，填充位置具有随机性.为使校验矩阵构造算法具有低编码复杂度，所构造的校验矩阵需具有图1的下三角结构，即与EBF构造算法相比，改进的EBF算法构造的校验矩阵具有一定的结构约束.在下三角区域，随着列号的增大，非0元素可填充的位置数量逐渐减少.若填充是沿着列号由小到大依次进行，则填充下三角区域时，随着列号的增大，可填充非0元素的位置数量越来越少，构成4环和6环等小环的可能性越来越大，从而影响构造算法性能.该点算法的改进主要是克服上述问题，随着列号的减小，构造非下三角区域时，对于每列来讲，非0元素可填充的位置因无结构束缚而有更多选择，从而降低4环和6环等短环的形成，从而提高了改进的EBF算法的纠错性能.

改进2 构造校验矩阵H的下三角部分的列时，每一列的首个GF(q)域上的非0元素必须添加在对角线的位置上，其余非0元素需添加在对角线下方.

该点对EBF算法的改进可保证所构造的矩阵具有如图1的下三角结构，矩阵中的GF(q)域上非0元素或分布在对角线上，或分布在对角线下方的区域，从而可采用具有线性编码复杂度的迭代编码方法进行编码，是改进EBF构造算法较EBF算法具有更低编码复杂度的关键.

改进3 按列重 (每列非0元素个数)递减的顺序依次将GF(q)域上的非0元素添加到校验矩阵H的非下三角部分的列中.

该点算法主要是保证改进的EBF算法构造的校验矩阵H具有更大的围长，从而提升纠错性能.对于校验矩阵来说，变量节点的度反映校验矩阵中每列非0元素的数量.对于非规则LDPC码，每列(行)中的非0元素数不同，即列重不同.列重越大，非0元素数量越多.由于该矩阵构造算法是逐次按列随机构造矩阵算法，若按照列重由小到大的顺序填充非下三角区域，随着列号的减小，每列中要填充的非0元素数量越来越多，又要保证填充的位置要满足girth约束条件，则等价于可填充非0元素的位置数量越来越少，构成4环和6环等小环的可能性越来越大，从而影响所构造算法的性能.该点算法的改进主要是为了克服上述问题，构造非下三角区域时，按照列重递减顺序添加H的每列，与列重由小到大的顺序相比，随着列号的减小，每列中非0元素的数量越来越少，在满足girth约束条件下，每列中可选择填充非0的位置数量要更多，从而避免4环和6环等短环的形成，因此可提高改进的EBF算法的纠错性能.

由于随机校验矩阵构造方法所构造的校验矩阵没有一定的结构性，因此本研究以式 (3)的64进制校验矩阵H8×16为例，说明所提出的改进的EBF算法构造出的校验矩阵的结构为

其中，比特节点的度分布序列为

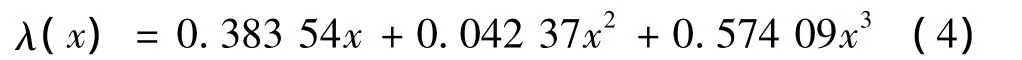
由于构造的矩阵具有下三角结构，构造时在满足式 (4)度分布的基础上，需将矩阵中最后一个比特节点的列重设为1.由式 (3)可见，最终构造的校验矩阵具有如图1的下三角结构，校验部分对角线上的元素均为1，对角线以上的元素均为0.因此可直接利用式 (1)进行迭代编码.

3 仿真结果及分析

图2是BEF构造算法中提出的改进1和改进3对改进的EBF算法的误码率性能的影响，即纠错性能的影响.其中，码率r=1/2;进制数q=64;信息位长为768 bit，即符号长为128，译码采用置信传播 (belief propagation，BP)译码算法，为给硬件实现提供参考，最大译码迭代次数取为32，调制方式为二进制移相键控 (binary phase shift keying，BPSK)调制，信道为高斯白噪声信道，比特节点服从式 (4)的度分布.图2中的4条仿真曲线分别为采用无改进的EBF、采用改进1、采用改进3及采用本研究提出的混合改进EBF算法 (改进1和改进3同时进行)的误码率曲线，3种改进EBF算法构造的校验矩阵均满足具有下三角结构 (满足改进2).由图2可见，在低信噪比(Eb/N0)的情况下，4条误码率曲线基本重合，表明纠错性能基本一致，但随着信噪比的增加，误码率出现明显差异.改进1、改进3和混合改进的EBF算法与未改进的EBF构造算法相比，对信噪比增益都有一定程度改善.其中，混合改进的EBF算法的编码增益提高最显著.当误码率为10－5时，有约为0.75 dB的编码增益.

图2 改进的EBF算法的误码率性能Fig.2 The bit error rate performance of improved EBF algorithm

上述4种LDPC码编码性能的差异是直接由构造的校验矩阵中短环的数量决定的.表1分别列出了4种矩阵中长度为4环和6环的数量.从表1可见，本研究提出的混合改进的EBF算法构造的矩阵的4环和6环平均数量最小，无任何改进构造的校验矩阵中4环和6环的平均数量最大.从图2可见，矩阵中的4环和6环的平均数量越少，所构造的LDPC码性能越佳.

表1 矩阵中的短环分布Table 1 Short loop distribution in the matrix

图3和图4分别显示了EBF及改进的EBF构造算法构造的多进制LDPC误码率和误帧率性能仿真曲线.其中，码率r=1/2;q分别为16和64;LDPC码的信息位长均为768 bit，即信息位的符号长度分别为192和128，译码采用BP译码算法，为给硬件实现提供参考，最大译码迭代次数取32，调制方式为BPSK调制，信道为高斯白噪声信道，比特节点服从式 (4)的度分布.EBF构造算法采用基于高斯消去的编码算法，而改进的EBF构造算法采用迭代编码算法.从图3和图4可见，采用改进EBF构造方法与直接应用EBF构造方法构造出的LDPC码的误码率、误帧率曲线基本重合，表明两个LDPC码编码增益基本一致，即本研究提出的改进的EBF算法与EBF算法构造的码字具有相同的纠错性能.

图3 改进的EBF与EBF构造方法构造的LDPC码的误码率性能Fig.3 The bit error rate performance of improved EBF and EBF algorithm

图4 改进的EBF与EBF构造方法构造的LDPC码的误帧率性能Fig.4 The frame error rate performance of improved EBF and EBF algorithm

4 编码复杂度分析

由对EBF算法的第2点改进可知，改进的EBF算法所构造的校验矩阵具有下三角结构，因而具有线性的编码复杂度，致使改进后的EBF算法在硬件实现上较原EBF算法更容易.EBF算法和改进的EBF算法的编码复杂度如表2.

表2 编码复杂度分析Table 2 Analysis of coding complexity

其中，n为码长;w为生成矩阵平均列重;k为信息位长.EBF算法构造的LDPC码的码字可采用基于高斯消去的编码算法，编码复杂度由两个部分构成，预处理的运算复杂度为o(n3)，编码复杂度为o(n2).而本研究提出的改进的多进制EBF构造算法可采用具有线性编码复杂度的迭代编码，当w相对于n可看作很小的常数时，该编码算法就具有线性复杂度.综上可知，由于两种算法的校验矩阵结构和采用的编码算法不同，系统的复杂度也不同.我们认为，这是由于高斯消去编码算法的复杂度取决于生成矩阵的稀疏性，虽然EBF算法构造的LDPC码校验矩阵非常稀疏，但其生成矩阵的非0元素密度大，因而编码复杂度正比于码长的平方.本研究提出的改进多进制LDPC码的EBF算法所构造的校验矩阵具有下三角结构，因而可以使用具有线性编码复杂度的迭代编码算法编码.

因此，本研究提出的改进EBF算法可在不损失LDPC码纠错性能的前提下，使系统的编码复杂度降低至线性.

结 语

本研究基于LDPC码的具有线性编码复杂度的迭代编码算法，提出了一种多进制LDPC码的EBF构造算法，通过改进编码方案和校验矩阵的构造来降低复杂度，并分别对改进的EBF和无改进的EBF算法所构造的多进制LDPC码进行了计算机仿真.结果表明，该改进EBF构造算法构造的LDPC码字与EBF构造算法构造的码字相比，可在不损失纠错性能的前提下，大幅降低系统的编码复杂度，从而为进一步的硬件实现提供了理论参考.但EBF算法属于随机构造LDPC码校验矩阵的构造算法，虽然具有纠错性能强于结构构造算法构造的码字的优点，但由于构造的矩阵具有随机性，因此硬件实现复杂度高于结构构造算法.虽然本研究提出的改进的EBF算法结合迭代编码算法可大大降低LDPC码的编码复杂度，但更适合于LDPC中短码的硬件实现.而对长码的硬件实现，复杂度仍然较高，此时可通过牺牲LDPC码一定的纠错能力，采用LDPC码校验矩阵的结构构造算法结合迭代编码算法来降低硬件实现复杂度.

/References:

［1］ Xue Rui，Zhao Danfeng，Xiao Chunli.Design of a receiver for LDPCC-CPM system based on Turbo principle［J］.Journal of Shenzhen University Science and Engineering，2010，27(3):301-305.(in Chinese)薛 瑞，赵旦峰，肖春丽.基于Turbo迭代算法的LDPCC-CPM系统接收机设计 ［J］.深圳大学学报理工版，2010，27(3):301-305.

［2］ Bennatan A，Burshtein D.Design and analysis of non binary LDPC codes for arbitrary discrete-memoryless channels ［J］.IEEE Transactions on Information Theory，2006，52(2):549-583.

［3］ Chen Chaoyu，Huang Qin，Chao Chichao，et al.Two low complexity reliability based message passing algorithms for decoding non-binary LDPC codes［J］.IEEE Transaction on Communications，2010，58(11):3140-3147.

［4］ Yu Y，Chen W.Design of low complexity non-binary LDPC codes with an approximated performance-complexity tradeoff［J］.IEEE Communications Letters，2012，16(4):514-517.

［5］ García-Herrero F，Canet M J，Valls J，et al.Serial symbol-reliability based algorithm for decoding non-binary LD-PC codes［J］.IEEE Communications Letters，2012，16(6):909-912.

［6］ Chen Xiaoheng，Lin Shu，Akella V.Efficient configurable decoder architecture for nonbinary quasi-cyclic LDPC codes［J］.IEEE Transactions on Circuits and Systems，2012，59(1):188-197.

［7］ He Kai，Sha Jin，Wang Zhongfeng.Nonbinary LDPC code decoder architecture with efficient check node processing［J］.IEEE Transactions on Circuits and Systems，2012，59(6):381-385.

［8］ Bennatan A，Burshtein D.On the application of LDPC Codes to arbitrary discrete-memoryless channels ［J］.IEEE Transactions on Information Theory，2004，50(3):417-438.

［9］ Li G，Fair I J，Krzymien W A.Low-density parity-check codes for space-time wireless transmission［J］.IEEE transactions on wireless communications，2006，5(2):312-322.

［10］ Wang Xuepeng，Bai Baoming，Ma Xiao.A low-complexity joint detection-decoding algorithm for nonbinary LDPC-coded modulation systems［C］//Proceedings on IEEE International Symposium on Information Theory.Austin(USA):Institute of Electrical and Electronics Engineers，2010:794-798.

［11］ Guo F，Hanzo L.Low complexity non-binary LDPC and modulation schemes communicating over MIMO channel［C］//The 60th Vehicular Technology Conference.Los Angeles(USA):Institute of Electrical and Electronics Engineers，2004，60(2):1294-1298.

［12］ Arabaci M，Djordjevic I B，Xu Lei，et al.Nonbinary LDPC-coded modulation for high-speed optical fiber communication without bandwidth expansion ［J］.IEEE Photonics Journal，2012，4(3):728-734.

［13］ Arabaci M，Djordjevic I B，XU Lei，et al.Nonbinary LDPC-coded modulation for rate-adaptive optical fiber communication Without bandwidth expansion［J］.IEEE Photonics Technology Letters，2012，24(16):1402-1406.

［14］ Lin Changyu，Djordjevic I B，Zou Ding，et al.Nonbinary LDPC-coded mode-multiplexed coherent optical OFDM 1.28-Tbit/s 16-QAM signal transmission over 2000 km of few-mode fibers with mode-dependent loss［J］.IEEE Photonics Journal，2012，4(5):1922-1929.

［15］ Zhou Bo，Kang Jingyu，Lin Shu，et al.High performance non-binary quasi-cyclic LDPC codes on euclidean geometries ［J］. IEEE Transactions on Communications，2009，57(5):1298-1311.

［16］ Arabaci M，Djordjevic I B，Saunders R，et al.Nonbinary quasi-cyclic LDPC-based coded modulation for beyond 100 Gb/s transmission ［J］.IEEE Photonics Technology Letters，2010，22(6):434-436.

［17］ Chen Chao，Bai Baoming，Wang Xinmei.Construction of nonbinary quasi-cyclic LDPC cycle codes based on singer perfect difference set［J］.IEEE Communications Letters，2010，14(2):181-183.

［18］ Zhang Li，Huang Qin，Lin Shu，et al.Quasi-cyclic LDPC codes:an algebraic construction，rank analysis，and codes on Latin squares［J］.IEEE Transactions on Communications，2010，58(11):3126-3139.

［19］ Zeng Linqi，Lan Lan，Tai Yingyu，et al.Constructions of nonbinary quasi-cyclic LDPC codes a finite field approach ［J］. IEEE Transactions on Communications，2008，56(4):545-554.

［20］ Kang Jingyu，Huang Qin，Zhang Li，et al.Quasi-cyclic LDPC codes:analgebraicconstruction［J］.IEEE Transactions on Communications，2010，58(5):1383-1396.

［21］ Wang Peng，Wang Xinmei.Study of efficient encoding of LDPC codes［J］.Journal of Xidian University Natural Science，2004，31(6):934-938.(in Chinese)王 鹏，王新梅.LDPC码的快速编码研究 ［J］.西安电子科技大学学报自然科学版，2004，31(6):934-938.

［22］ Campello J，Modha D S.Extended bit-filling and LDPC code design［C］//IEEE Global Telecommunications Conference.San Jose(USA):IBM Almaden Research Center，2001，2:985-989.

［23］ Tarokh V，Jafarkhani H，Calderbank A R.Space-time block coding for wireless communications:performance result［J］.IEEE Journal on Selected Areas in Communications，1999，17(3):451-460.