非平衡集成迁移学习模型及其在桥梁结构健康监测中的应用

于重重，吴子珺，谭励，涂序彦，田蕊

(1.北京工商大学计算机与信息工程学院，北京100048;2.北京科技大学 计算机与通信工程学院，北京100083)

随着智能监测方法与评估技术的不断发展，桥梁结构健康监测及状态评估的研究逐渐成为热点.为了对桥梁的安全和维护提供有力保障，通常需要连续监测桥梁静应变、沉降等数据，同时必须保证监测数据的真实可靠.但通常存在一些干扰因素，如传感器损坏、异常受力、天气条件恶劣等，会造成监测数据的间断性异常或缺损，从而无法对所获得的监测数据进行有效的数据分析［1-2］.因此，利用相似的辅助测点数据，实现对有效数据量少的目标测点的建模与分析，是解决上述问题的重要思路.

迁移学习是一种强调在相似但不完全相同的领域、任务和分布之间实现知识转化的学习方式.本文针对桥梁监测数据的间断性异常或缺损的特点，将迁移学习引入到桥梁结构健康监测领域，通过建模分析，解决目标测点实测有效数据过少时的数据分类和预测问题.文中提出了一个改进的迁移模型，首先通过对原始监测数据进行预处理，得到能够表征数据变化规律的训练数据集，然后再利用相似性度量函数，完成对具有相似数据变化规律的测点聚类，最后运用非平衡集成迁移学习算法(the unbalanced integrated transfer learning algorithm，UBITLA)［3］建立桥梁结构健康监测的分类模型，利用过往监测数据模型的迁移对新数据进行预测，以达到对监测数据的类别划分和评定桥梁结构损伤级别的目的.

1 迁移学习的基本理论

迁移学习作为机器学习和人工智能领域研究的新方向，近年越来越受到关注.迁移学习强调的是区域、任务、分布相似但不相同的知识的传递［4-5］，其突破了传统数据挖掘的两大假设:一是训练数据与测试数据必须同概率分布;二是两者必须同特征空间.然而，随着对迁移学习的研究，不同学者对迁移学习中存在的一些缺陷，提出了很多解决问题的算法，并得到了有效的应用.如运用基于EM的跨语言文本分类算法用以解决跨特征空间的迁移学习问题［6］，基于朴素贝叶斯分类器的支持跨领域文本分类的分类器实现了不同领域文本之间知识的迁移问题［7］，基于TrAdboost算法解决对称的二分类问题等［8-9］.这些成功的应用推动了迁移学习在处理新任务中标记数据量小的问题中的迅猛发展.

在桥梁结构健康监测领域，监测数据存在以下特点:

1)不同类别的样本分布极度不平衡，差异大;

2)辅助数据中存在大量的与目标数据集不相似的冗余信息;

3)桥梁实际监测的表征结构健康的正数据和表征结构损伤的负数据分布极度不平衡，负样本数量远远小于正样本，但负样本对于桥梁健康监测影响很大.因此，对于桥梁结构的损伤判定可以将其看作是一个非对称的二分类问题.

本文将迁移学习引入到桥梁结构健康监测领域，利用已有监测点数据，基于非平衡集成迁移学习算法(UBITLA)，提出了一种改进的迁移学习模型，该方法能够有效地解决桥梁结构健康监测中存在的实际问题.

2 改进的迁移学习模型在桥梁结构健康监测中的应用

2.1 改进的迁移学习模型描述

本文提出的迁移学习模型总体思路如下:1)将桥梁结构健康监测系统中监测到的原始数据进行预处理，其中包括信息筛选、去冗余、去噪声以及去除重复数据;2)对预处理后的监测数据，根据测点间的相似度，对具有相似变化规律的测点进行聚类;3)对聚类结果使用非平衡集成迁移学习算法，建立针对目标测点的数据分类模型，对目标数据集中的无标签数据进行预测分类，以实现对监测数据进行类别划分，评定桥梁各级损伤情况的目的.总体流程图如图1所示.

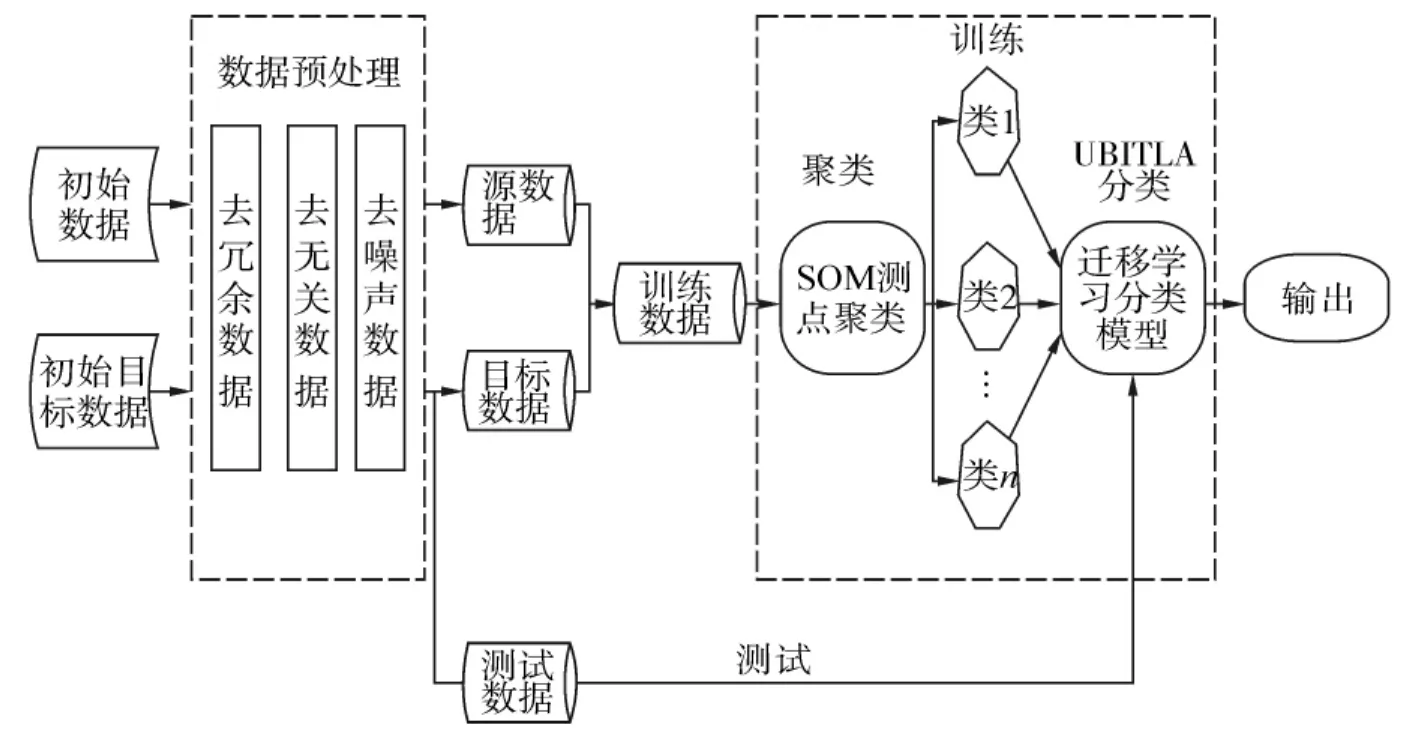
图1 改进的迁移学习模型Fig.1 Improved transfer learning model

2.2 基于相似测点的SOM聚类

相似度函数是聚类的前提条件，这是由于分类是将相似的模式样本聚为一类.因为数据存在不同的类型，所以有不同的方法计算相似度，如欧氏距离、切比雪夫距离、曼哈顿距离、明氏距离、加权的明氏距离、马氏距离、夹角余弦函数等［10］.在自组织映射(self-organizing map，SOM)算法中经常使用相似度函数作为分类的基础.SOM算法是一个由全连接的神经元阵列组成的无导师的自组织、自学习网络，是神经网络用于解决聚类问题的典型应用［11-12］.

由于桥梁结构健康监测系统所获得的监测数据受突发应力与异常负载等影响，经常会出现个别监测点数据存在异常，如果使用上述方法难以有效克服个别维度的干扰，且易受到高维特性的干扰，若存在2个数据的个别维度上的值差异过大或过小，这会影响整体度量效果，使数据间的相似信息被这少数维度的过大差异所淹没［13-14］.因此为减小这些异常数据对整体数据的影响，对传统的距离度量函数进行修改，从根本上解决传统的相似度度量函数在高维数据空间中存在的不足，有效地缓解大差异个别维度对相似度的影响，具体如下.

定义1 设有d维数据向量X=(x1，x2，…，xd)及 Y=(y1，y2，…，yd)，则相似度度量函数(similarity measurement points clustering，SMPC)如式 (1)所示:

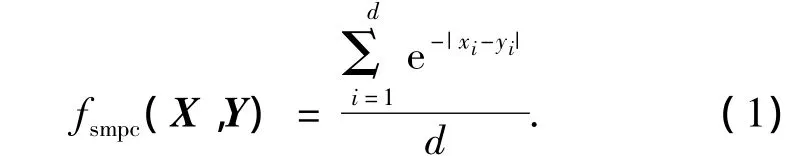
改进后的相似度度量函数通过引入指数e，实现了在xi与yi大差异的情况下，分子数值变小的需求.通过对比计算发现，改进后的相似度度量函数SMPC对比于传统的相似性度量函数，具有如下性质:

1)新函数充分考虑了2个数据向量间的所有维度，使大差异维度的贡献率降低;

2)新函数的最大值为1，代表X和Y在所有维度上的值都相等，此时X和Y在d维空间上是完全重合的，相似度最大.若最小值为0，则代表X和Y在每个维度上的差异均接近于无穷大，此时X和Y相似度最小.

通过基于SMPC相似度度量函数的SOM网络，完成对桥梁监测点的聚类，其具体训练步骤如下:

1)初始化SOM网络结构，对神经元权值向量随机赋初值;

2)随机选择输入样本;

3)计算各神经元之间的相似度，选择具有最大相似度的神经元作为获胜神经元;

4)使用单调递减函数对获胜神经元及其邻域范围内的神经元的权值进行调整;

5)对算法的收敛性进行判断，若不满足收敛条件则重复上述步骤3)直至算法达到收敛.

2.3 UBITLA 算法

针对桥梁结构健康监测系统表征桥梁结构健康与否的正、负数据分布极度不均衡，若对其施行相同的权值调整策略会由于稀缺类样本权值的迅速减小而导致训练的失败问题，因此模型采用非平衡样本分类的集成迁移学习算法UBITLA进行处理.算法在TrAdaboost算法的基础上，通过改变稀缺类样本权值的调整策略，使其不会迅速变小，从而保证这部分样本对模型建立的贡献率;另外该算法还引入冗余数据动态剔除策略，适时剔除辅助训练数据集中的冗余数据，以确保训练数据的高质.UBITLA算法流程如图2所示.

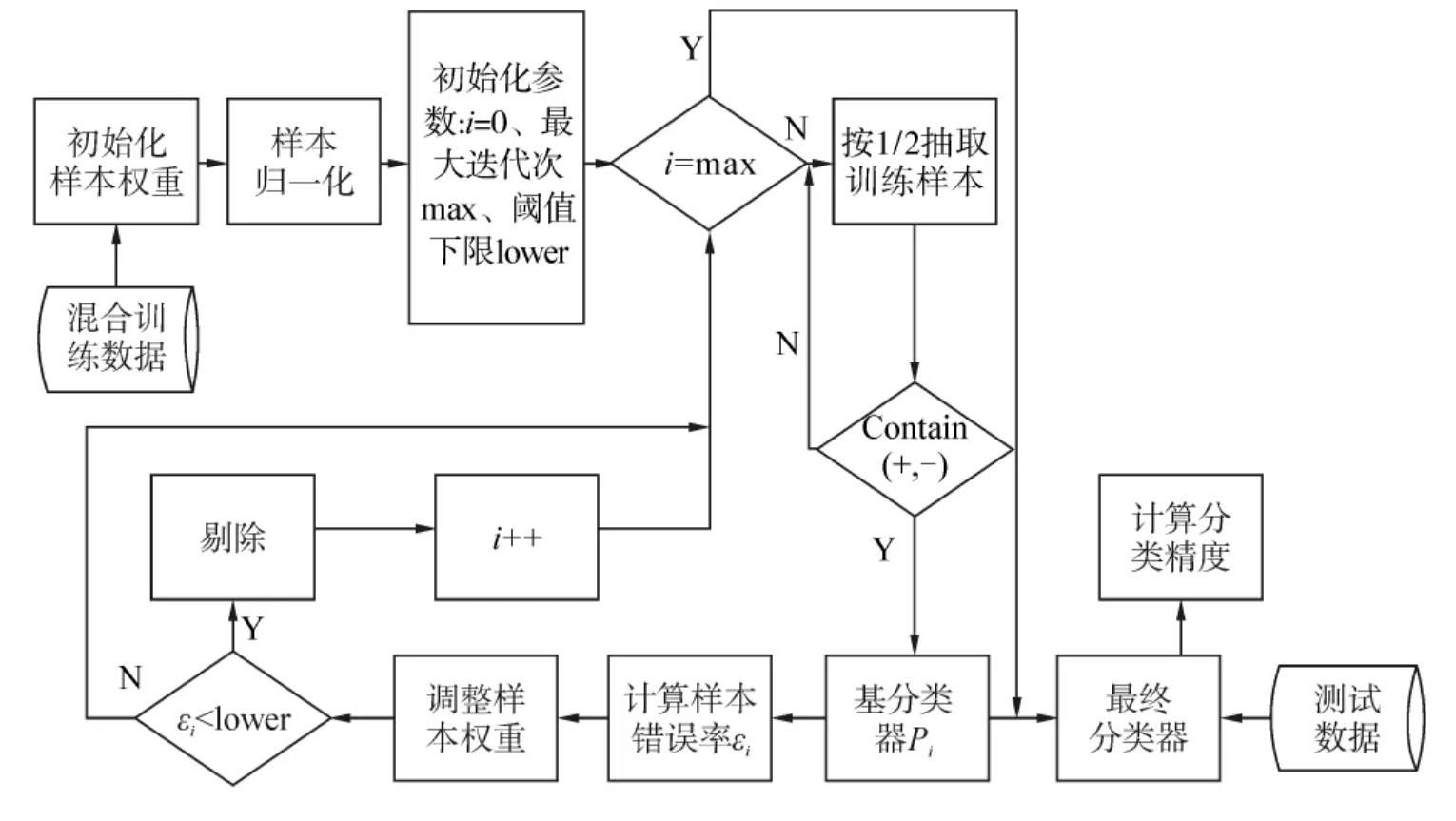
图2 UBITLA算法Fig.2 UBITLA algorithm

UBITLA算法的主体思想为:将迁移辅助数据集A与目标数据集O按比例抽取部分数据后混合成训练数据集C，并通过初始化样本权重与归一化样本完成对原始样本的预处理;然后在每次的训练结果中选择误差最小的弱分类器ht，经T轮迭代后得到弱分类序列h1，h2，…，ht;最终将多个弱分类器叠加起来得到一个强分类器.

3 实验结果与分析

3.1 实验样本数据

实验采用已有2年监测历史的杭州湾大桥作为研究对象，选用某天6:00—20:00共20个测点所测得的相邻时段的数据差值作为实验数据，其中包含了早、中、晚3个高峰时段，以及上、下午低峰时段的数据变化情况，并分别从各数据类型中抽取一定数目的数据按比例组成初始数据集S1和初始目标数据集S2，其具体组成如表1所示.

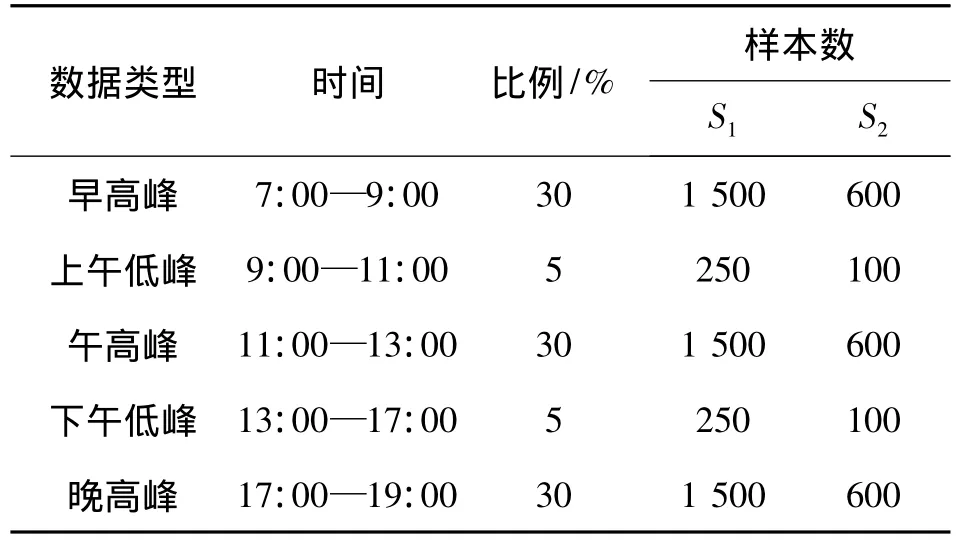
表1 实验数据组成描述Table 1 Description of the experimental data

其中，正负样本比例为5∶1;输入数据为以1 h为监测周期，采集当日从6:00—20:00共14 h的静应变数据，并组成具有14维的属性向量(其包含监测数据在1 d内的变化情况).在训练过程中从S1内随机抽取1/2的数据，经数据预处理后作为源数据集Y1，同样从S2内分别随机抽取1/2的数据，经数据预处理后作为目标数据集G1与测试数据集T1，并通过由源数据集Y1与目标数据集G1所组成的训练数据完成对迁移学习模型的训练，实现对目标数据集T1中无标签数据的预测分类，这样就可以通过监测数据的类别来评定桥梁的级别损伤.

3.2 结果与分析

3.2.1 不同距离函数

通过对训练数据采用不同的相似度距离函数的SOM网络完成对监测点的聚类，其聚类结果如表2所示，其中 D(2)(x，y)为欧式距离的相似性度量函数.

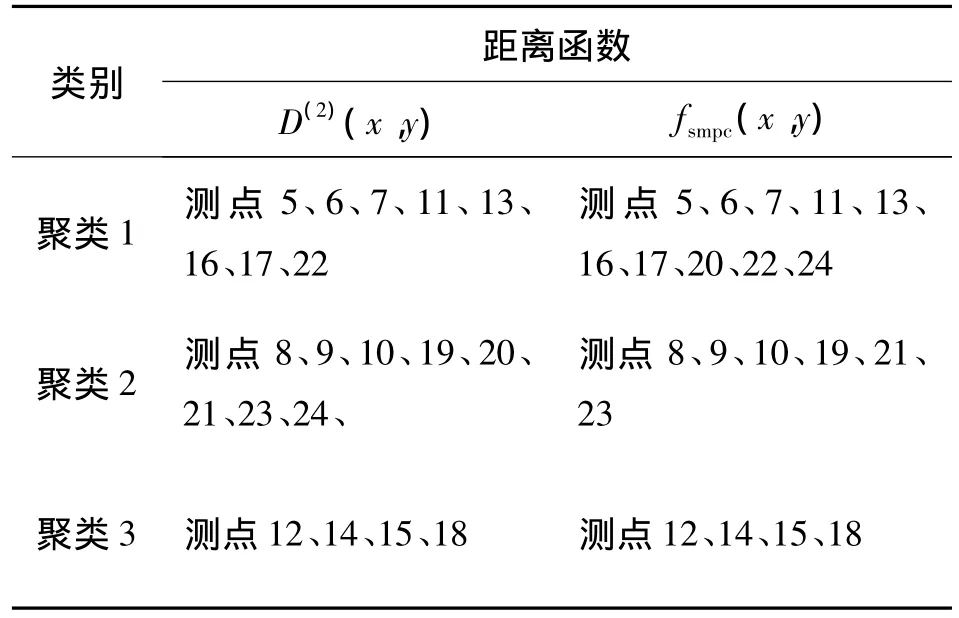
表2 杭州湾大桥沉降数据监测点聚类Table 2 Hangzhou Bay Bridge settlement data monitoring points clustering

然后将上述2种不同的聚类结果，应用UBITLA迁移学习算法建立针对目标数据的分类模型，完成对目标数据中无标签数据的预测分类.采用欧式距离作为相似度距离函数与采用SMPC相似度距离函数的SOM网络聚类结果，对迁移学习模型分类精度的影响如图3所示.

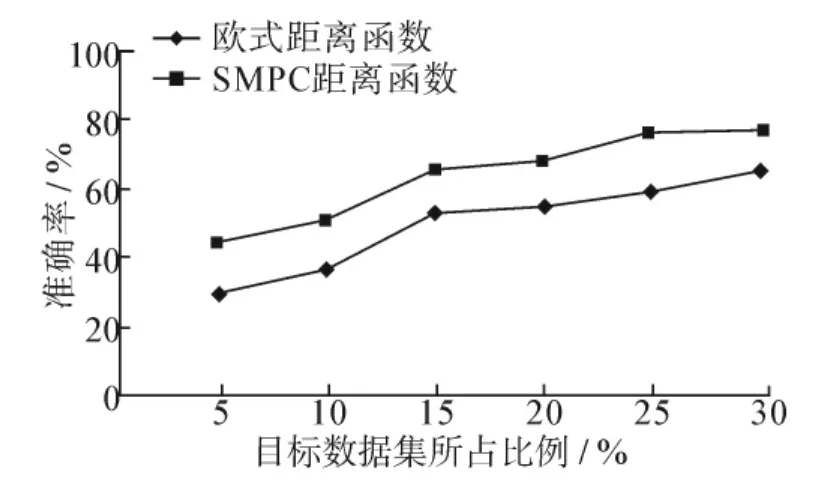
图3 2种不同的距离函数对迁移学习模型分类精度的影响Fig.3 Effects of two different distance functions on migration learning model classification accuracy

从上述的结果来看，2种度量函数的总体聚类效果基本相近，但是对于个别测点，如杭州湾大桥的20号测点，在采用欧式距离作为相似度距离函数的SOM网络的聚类结果中将其分入了类别2中，而在采用SMPC相似度距离函数的SOM网络的聚类结果中将该测点分入了类别1中.通过对该测点和所在类别特点的进一步分析发现，该测点只是在某2个维度上的数据波动较大而在其余的12个维度的波动均比较小.由于传统的距离函数将所获得的14维数据向量都均等看待，放大了个别维度中异常数据所造成的影响，因此影响了整个聚类结果的合理性;但是本文提出的SMPC距离函数克服了传统度量函数的这一缺陷，使得聚类结果更接近实际.因此，采用SMPC距离函数所获得的迁移学习模型分类精度高于传统的欧式距离函数.

3.2.2 辅助数据集的加入

选择杭州湾大桥测点20作为目标分类测点，分别选择同类辅助测点5和异类辅助测点8作为辅助训练测点，代入UBITLA算法进行训练.辅助数据集对迁移学习模型分类精度的影响如图4和5所示.

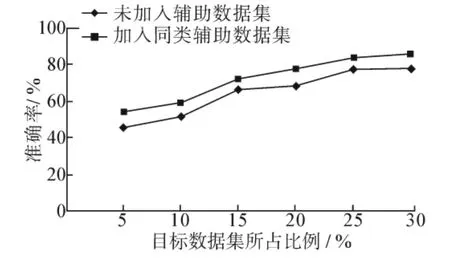
图4 同类辅助数据集的加入对迁移学习模型分类精度的影响Fig.4 Effects of similar auxiliary data sets on migration learning model classification accuracy

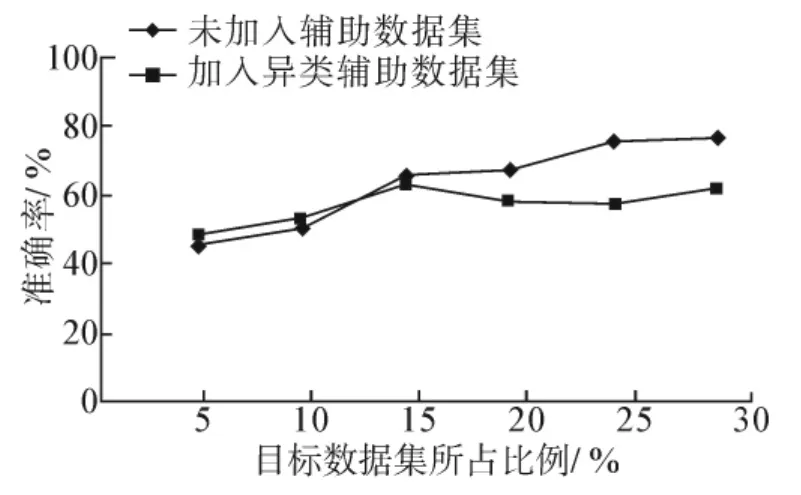
图5 异类辅助数据集的加入对迁移学习模型分类精度的影响Fig.5 Effects of heterogeneous auxiliary data sets on migration learning model classification accuracy

实验结果表明，同类辅助数据集的加入可以有效地帮助目标数据的学习，随着目标数据集比例的增加，迁移学习模型分类精度不断提高;异类辅助数据集的添加，有时会对目标数据的学习起到促进作用，但是随着目标数据集所占比例的增加会出现相反的情况，这可能是由于异类辅助数据集数据与目标数据差异性较大，对迁移学习模型分类精度造成了一定的消极影响，导致分类精度下降.总之，引入同类辅助数据集能够有效地在辅助数据与目标数据间进行知识迁移，提高对目标数据的学习效率和迁移学习模型分类的准确性.

4 结束语

本文围绕迁移学习的基本理论和在数据分类问题中的应用，针对桥梁健康监测中监测数据存在的问题，提出了一个改进的迁移学习模型，并且介绍了模型总体思路和关键技术.通过对现役桥梁的监测数据的实验，证明了该模型的有效性.随着技术的创新、方法的完善，迁移学习在不久的将来会应用在不同的领域上，期待其有更好的创新.

［1］刘永前.大型桥梁结构健康监测技术研究与应用［D］.北京:北京交通大学，2007:1-12.LIU Yongqian.Research and application on structural health monitoring of long-span bridge［D］.Beijing:Beijing Jiaotong University，2007:1-12.

［2］李鹏飞，吴太成.桥梁健康监测技术研究综述［J］.建筑监督检测与造价，2010，7(7):28-31，40.LI Pengfei，WU Taicheng.A review of health monitoring techniques of bridge［J］.Supervision Test and Cost of Construction，2010，7(7):28-31，40.

［3］于重重，田蕊，谭励，等.非平衡样本分类的集成迁移学习算法［J］.电子学报，2012，40(7):1358-1363.YU Chongchong，TIAN Rui，TAN Li，et al.Integrated transfer learning algorithmic for unbalanced samples classification［J］.Acta Electronica Sinica，2012，40(7):1358-1363.

［4］许至杰.迁移学习理论与算法研究［D］.上海:华东师范大学，2012:4-10.XU Zhijie.Research about the theories and algorithms of transfer learning［D］.Shanghai:East China Normal University，2012:4-10.

［5］戴文渊.基于实例和特征的迁移学习算法研究［D］.上海:上海交通大学，2008:14-21.DAI Wenyuan.Instance-based and feature-based transfer learning［D］.Shanghai:Shanghai Jiao Tong University，2008:14-21.

［6］UNKELBACH J，YI S，SCHMIDHUBER J.An EM based training algorithm for recurrent neural networks［J］.Proceedings of the 19th International Conference on Artificial NeuralNetworks. Berlin/Heidelberg:Springer-Verlag，2009:964-974.

［7］DAI Wenyuan，XUE Guirong，YANG Qiang，et al.Transferring naive Bayes classifiers for text classification［C］//Proceedings of the 22nd National Conference on Artificial Intelligence.Vancouver，Canada，2007:540-545.

［8］RAINA R，BATTLE A，LEE H，et al.Self-taught learn-ing:transfer learning from unlabeled data［C］//The Twenty-fourth International Conference on Machine Learning.Corvallis，USA，2007:759-766.

［9］刘伟，张化祥.数据集动态重构的集成迁移学习［J］.计算机工程与应用，2010，46(12):126-128.LIU Wei，ZHANG Huaxiang.Ensemble transfer learning algorithm based on dynamic dataset regroup［J］.Computer Engineering and Applications，2010，46(12):126-128.

［10］邵昌昇，楼巍，严利民.高维数据中的相似性度量算法的改进［J］.计算机技术与发展，2011，2(2):7-10.SHAO Changsheng，LOU Wei，YAN Limin.Optimization of algorithm of similarity measurement in high-dimensional data［J］.Computer Technology and Development，2011，2(2):7-10.

［11］杜俊卫，李爱军.一种基于聚类的文本迁移学习算法［J］.计算机系统应用，2010，19(12):238-241.DU Junwei，LI Aijun.Transfer learning algorithm for text classification based on clustering［J］.Computer Systems ＆ Applications，2010，19(12):238-241.

［12］戴群，陈松灿，王喆.一个基于自组织特征映射网络的混合神经网络结构［J］.软件学报，2009，20(5):1329-1336.DAI Qun，CHEN Songcan，WANG Zhe.Hybrid neural network architecture based on self-organizing feature maps［J］.Journal of Software，2009，20(5):1329-1336.

［13］王戒躁，钟继卫，王波.大跨桥梁健康监测系统设计构成及其进展［J］.桥梁建设，2009(增刊2):11-16.WANG Jiezao，ZHONG Jiwei，WANG Bo.Designed components and development of health monitoring systems for long span bridges［J］.Bridge Construction，2009(S2):11-16.

［14］于重重，杨扬，涂序彦，等.DBSCAN算法在桥梁健康监测预测模型中的应用［J］.计算机工程与应用，2008，44(12):224-227.YU Chongchong，YANG Yang，TU Xuyan，et al.Application of DBSCAN algorithm in bridge-health monitoring prediction model［J］.Computer Engineering and Applications，2008，44(12):224-227.