改进的萤火虫算法求解阻塞流水线调度问题

郭丽萍，李向涛，谷文祥，2，殷明浩

(1.东北师范大学计算机科学与信息技术学院，吉林长春130117;2.长春建筑学院基础教学部，吉林长春130607)

流水线调度问题是一类重要的组合优化问题，阻塞流水线调度问题作为其中的一个重要分支，由于具有很强的工程背景和实际意义，而得到了越来越多学者的关注，目前人们已经证明包含2台机器以上的阻塞流水线调度问题的计算复杂性为NP-hard［1］.该问题的解决方法主要分为构造性启发式方法［2-3］和元启发式方法［4-7］.萤火虫算法［8］是由剑桥大学的Yang在2008年提出来的一个模拟自然界中萤火虫发光行为的仿生算法，目前该算法在函数优化方面表现出较优的性能［9］.为了使萤火虫算法适用于求解阻塞流水线调度问题，本文对萤火虫算法进行了一些改进，加强了算法的搜索性能，且避免了萤火虫算法早熟的问题.

1 阻塞流水线调度问题

阻塞流水线调度问题可以描述为:n个作业J1，J2，…，Jn要在 m 台机器 M1，M2，…，Mm上运行，每个作业包含m道工序，每个作业的工序必须按照统一顺序在m台机器上执行，每个作业在每台机器上的运行时间是固定的，要求协调不同作业的执行顺序，使得某种生产性能指标达到最优.阻塞流水线调度问题的约束条件包括如下:

1)每个作业在每台机器上只能加工1次;

2)每台机器每次最多只能加工1道工序;

3)每台机器上的作业加工顺序相同;

4)作业的某道工序在某台机器上的加工一旦开始，便不能终止;

5)一个作业完成某道工序后，该作业将在当前机器上滞留直到下游机器变为可用为止.

在该问题中，用 π ={π1，π2，…，πn}表示一个调度序列，oj，k(j=1，2，…，n;k=1，2，…，m)表示作业j在机器k上执行一个无间断的工序，其所需时间为 pj，k(j=1，2，…，n;k=1，2，…，m)，ej，k(j=1，2，…，n;k=0，1，…，m)表示第j个作业在第k台机器上的离开时间.则有:

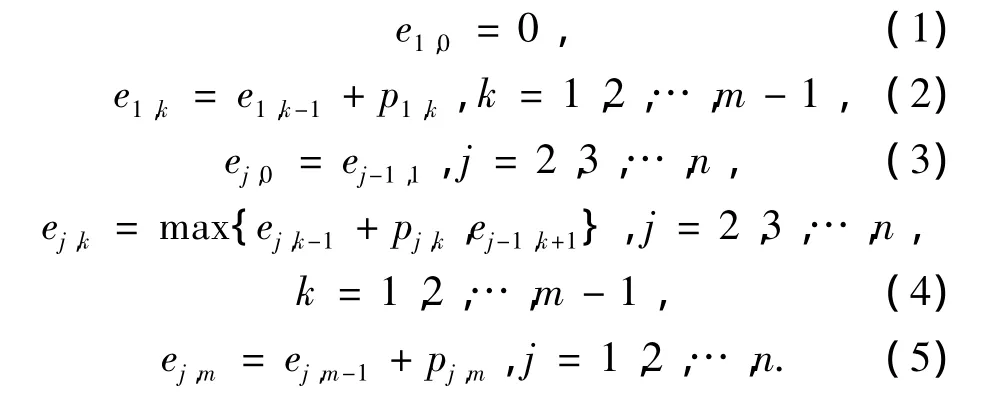
本文选取最大完工时间最小为优化指标，那么最大完工时间Cmax(π)=en，m，且它的计算复杂性为O(mn).

以3个作业J1、J2、J3为例，下面举例说明如何求解阻塞流水线调度问题，3个作业在3台机器上运行所需时间如表1所示.第1个作业在第1台机器上运行所需要的时间为3，第1个作业在第2台机器上运行所需要的时间为4，依此类推.

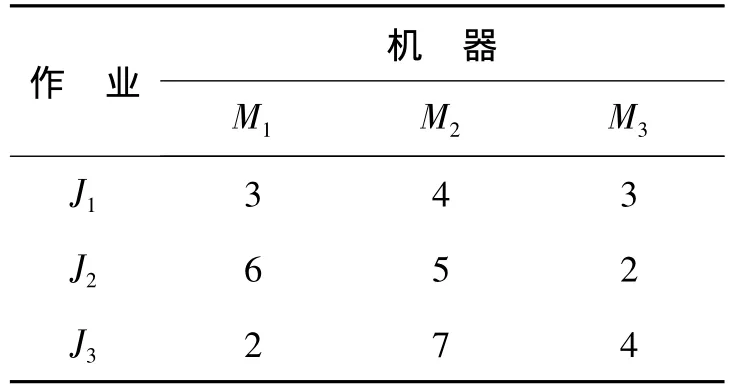
表1 时间矩阵Table 1 Time matrix of an example

由式(1)～(5)可以计算出该问题的最大完工时间的最小值 e3，3为21，对应的作业执行顺序为{J3，J2，J1}，如图 1 所示.

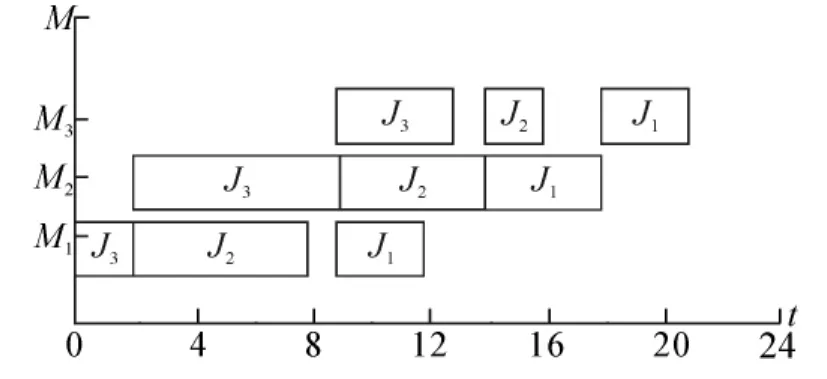
图1 问题的甘特图表示Fig.1 The Gantt chart of the example

2 萤火虫算法

萤火虫算法是一种通过模拟自然界中萤火虫发光行为的仿生算法.目前，人们对自然界中萤火虫的发光行为的意义还存在很多争议，不过有2点是确定的:吸引配偶和吸引潜在的猎物.

一般情况下，可见光的强度随着当前位置到光源距离的增大而减小，另外，空气还要吸收一部分光源.因此，萤火虫发出光只在一定的距离范围内可以被其他萤火虫看见.萤火虫算法约定［9］:1)萤火虫之间不存在性别之分，每只萤火虫都可以吸引其他的萤火虫，也可以被其他的萤火虫吸引;2)萤火虫的吸引力和它们发出的光的亮度成正比，因此，对于任意2只萤火虫来说，亮度较弱的萤火虫会朝着亮度较强的萤火虫飞行;如果当前可见光距离范围内，没有比自己更亮的萤火虫时，则该萤火虫实行随机飞行策略;3)光的亮度一般由求解问题的目标函数决定.

在萤火虫算法中，每只萤火虫称为一个“个体”，每个个体包含亮度、吸引力、位置等属性.在该算法中，个体在某个固定位置的亮度I是固定的，该变量的设定取决于具体问题的目标函数.其他个体看到该个体的亮度则随着它们之间距离的增大而减小，此外，传播介质也会吸收一部分光线，因此，个体在距离当前位置r处的亮度还和介质的吸收率有关［9］.一般把一个个体在距离该个体r处的亮度表示为

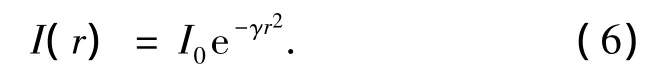
式中:I0为个体在当前所处位置的亮度，γ为介质的吸收率.有时，为了减小个体亮度变弱的速率，式(6)也可用如下公式代替:

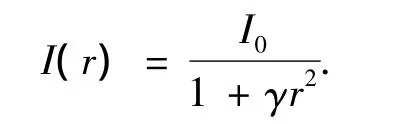
每个个体对其他个体的吸引力β也是相对的，它随着2个个体之间距离的增大而减小;此外，吸引力还和介质的吸收率有关［9］.因此把个体在距离该个体为r的位置对其他个体的吸引力定义为

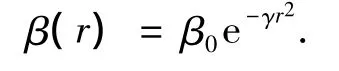
式中:β0表示2个个体距离为0时，当前个体对另外1个个体的吸引力，γ为介质的吸收率.

在该算法中，2个个体之间的距离r采用欧式距离.个体i向着比它更亮的个体j进行更新的公式定义为

式中:xi和xj分别表示个体i和个体j在整个种群更新之前的位置，x'i表示个体i朝着比自己更亮的个体j更新之后的位置，rij代表个体i和个体j之间的距离，β0e－γr2ij表示个体 j对个体 i的吸引力，α 是一个［0，1］内的随机数，R为一个随机数生成函数，生成［0，1］内的随机数.

3 改进的萤火虫算法求解阻塞流水线调度问题

虽然萤火虫算法在函数优化方面表现出了较好的计算性能，但是，它在求解阻塞流水线调度问题中仍然存在早熟现象，为了提高算法的寻优性能，本文对萤火虫算法进行了一些改进.

萤火虫算法应用于求解阻塞流水线调度问题时，首先遇到的问题就是如何将实数编码离散化.本文提出一种最小排序方法，这种方法可以将个体的实数编码形式转化成离散的调度序列.该方法对初始化后的实数序列从小到大进行排序，它们的排序序号构成一个离散序列，将这个序列作为该实数序列对应的离散调度序列.如表2所示，0.43是实数编码序列中最小的实数，从小到大排序后，它的序号应该为1;同理，0.91是实数序列中最大的，因此其序号为5.新生产的序列{4，2，5，1，3}作为实数序列{0.85，0.56，0.91，0.43，0.76}对应的离散调度序列.

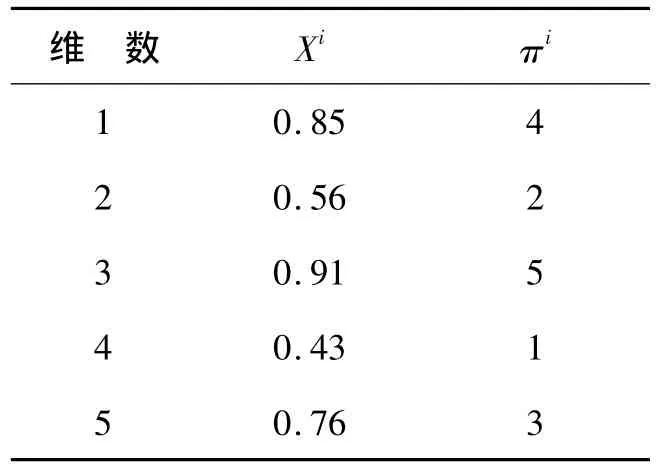
表2 个体表示形式Table 2 The presentation of an object

其次，在种群初始化时，本文设计了一种双重初始化方法:分别生成2个种群，计算2个种群中每个个体的最小完工时间.让2个种群中的个体按序号两两进行比较:种群1中的第1个个体和种群2中的第1个个体进行比较，选择其中最小完工时间较小的个体，作为新种群的第1个个体;种群1中的第2个个体和种群2中的第2个个体进行比较，选择其中最小完工时间较小的一个，作为新种群的第2个个体;依此类推，新种群作为初始化种群.此外，由于 NEH(Nawaz-Enscore-Ham)［10］启发式算法是目前求解流水线调度最有效的启发式方法之一，因此，在初始化种群时还引入了NEH的思想.种群的第1个个体由NEH启发式方法生成，其他个体由双重初始化方式生成，从而使得算法有一个较好的初始化环境.

目前，人们已经发现很多昆虫存在莱维飞行(Lévy flights)［11-12］，且莱维飞行已经应用于优化领域，并取得了预期的良好效果.为了增强算法的全局搜索性能，避免种群陷入局部最优，在萤火虫算法的搜索过程中，如果当前个体找不到比自己更优的个体时，选择莱维飞行代替原算法中的随机飞行.此外，对于那些种群中非最优的个体，对它们的飞行公式进行改进:当它们发现比自己更亮的个体时，首先由系统产生一个随机数q，如果q小于0.5，则按照式(8)进行更新;否则，仍采用式(7)对个体的位置进行更新.

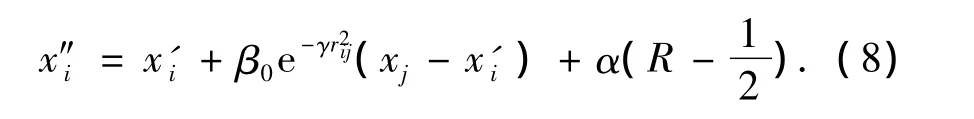
式中:xj仍然表示个体j在整个种群更新之前的位置，x'i表示的是第i个个体朝着前j－1个体中比自己亮的个体更新之后的新位置，x″i表示x'i朝着比自己亮的个体j更新之后的位置，rij代表个体i和个体j之间的距离，β0e－γr2ij表示个体 j对个体 i的吸引力.可以看出，式(8)是实时更新的，式(7)仅仅依赖于整个种群移动之前的个体位置.这样的飞行更新方式能够增加飞行的随机性，有利于保持种群的多样性，增大种群搜索空间.

为了加速种群的收敛，本文还提出了一种α的更新方式，使得α随着迭代次数逐渐减小，更新公式为

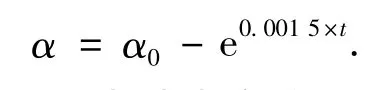
式中:α0选用0.9，t为迭代次数.

对于一个调度序列而言，目前主要有3种产生新序列的方法:插入、交换和逆序［6］.其中，插入方法被证明为最适合产生一个新序列的方法.为了加强萤火虫算法的局部搜索能力，本文引入了一个局部搜索算法.局部搜索算法可以描述如下［7］:

2)i=i+1，如果 i＞n，则 i=i－n.

3)把πr赋给中间序列U，把序列U中的第i个作业从U中去除，将插入U中所有可以插入的位置，选取其中最好的调度序列πbest.

4)分别求解序列πbest和序列U的最小完工时间 f(πbest)和 f(U)，如果 f(πbest)＜f(U)，则 U=πbest，j=0;否则 j=j+1.

5)如果 j≤n，转步骤2);否则，算法结束，πr=U.

在这个算法中，i和j用来控制循环次数，没有实际意义，n是作业的数目，也是解的维数.

这种局部搜索算法的好处在于:首先，局部搜索策略并没有直接对所选序列进行修改，而是应用于一个中间序列U，避免算法陷入局部最优;其次，在每次搜索过程中，只有找到更好的解时，才对中间序列进行更新，有利于算法逐步向更优的解靠近.因此，局部搜索算法在一定程度上加强了萤火虫算法的局部搜索能力.

改进后的萤火虫算法和原算法相比，初始化部分使得算法有一个较好的搜索域，局部搜索算法又进一步提高了算法的搜索性能.改进后的萤火虫算法求解阻塞流水线调度问题的步骤如下:

1)初始化种群，包括迭代次数t=0、最大迭代次数tmax、随机参数 α0、个体吸引力 β0、介质吸收率γ、局部搜索概率p.

2)按照式(1)～(5)计算每个个体的最小完工时间.

3)萤火虫算法.

①更新α;

②对当前个体，如果有比自己更亮的个体，则按照改进后的更新方式，利用式(7)或(8)对当前个体的位置进行更新;否则，采用莱维飞行对个体位置进行更新.

4)按照式(1)～(5)计算每个个体的最小完工时间.

5)系统产生一个随机数，如果这个随机数小于局部搜索概率p，则对种群个体进行局部搜索，并更新种群.

6)t=t+1，如果t≥tmax或算法达到其他标准，则算法终止;否则，转步骤3).

4 仿真实验

实验所用PC机的处理器为AMD Athlon64 X2 3600+1.91 GHz，内存为 960 MB，编程工具采用Matlab 7.0.

4.1 数据集

本文采用著名的Taillard数据集作为测试实例，该数据集包含12个子集，每个子集包含10个测试实例.为了检验算法的有效性，从这些子集中选取了部分具有代表性的实例作为测试数据，所选实例涵盖了从20个作业5台机器到200个作业10台机器不同难度的测试实例，具有很好的代表性.所选实例的规模如表3所示.例如在Ta04实例中，20×5表示20个作业在5台机器上运行.

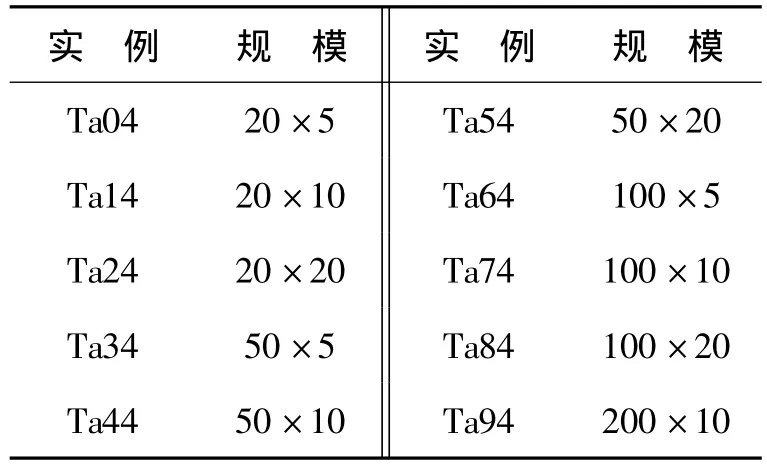
表3 实例规模Table 3 The size of instances

4.2 实验结果及分析

实验中，种群大小为10，最大迭代次数tmax为100，α0、β0、γ 的设置参考了萤火虫算法相关文献［9，13-14］中的参数设置，α0设置为 0.9，β0设置为1.0，γ 设置为 0.9，局部搜索概率 p 设置为 0.2.对于前6个实例，每个实例进行10次独立实验;对于后4个实例，由于数据量较大，每个个体进行5次独立实验.为了测试改进后的萤火虫算法在阻塞流水线调度问题中的性能，还对同等条件下的未改进的萤火虫算法和标准的粒子群算法进行了测试.表4为未改进的萤火虫算法的测试结果，表5为标准粒子群算法的测试结果，改进的萤火虫算法的测试结果列于表6中.其中，在标准的粒子群算法中，2个学习因子c1和c2取值为2，惯性权重 ω设置为 0.7.

由表4、5可以看出，无论是最小值、最大值，还是平均值，萤火虫算法的求解结果普遍优于标准粒子群算法.对比表4和表6，可以发现，改进的萤火虫算法在求解效果上要远远优于基本的萤火虫算法，而且求解结果更加稳定.综合表4～6，改进后的萤火虫算法的求解效果明显优于基本的萤火虫算法和标准的粒子群算法.并且随着种群的增大，这种差距更加明显，充分体现了算法的有效性，而且新算法的求解效果更加稳定.

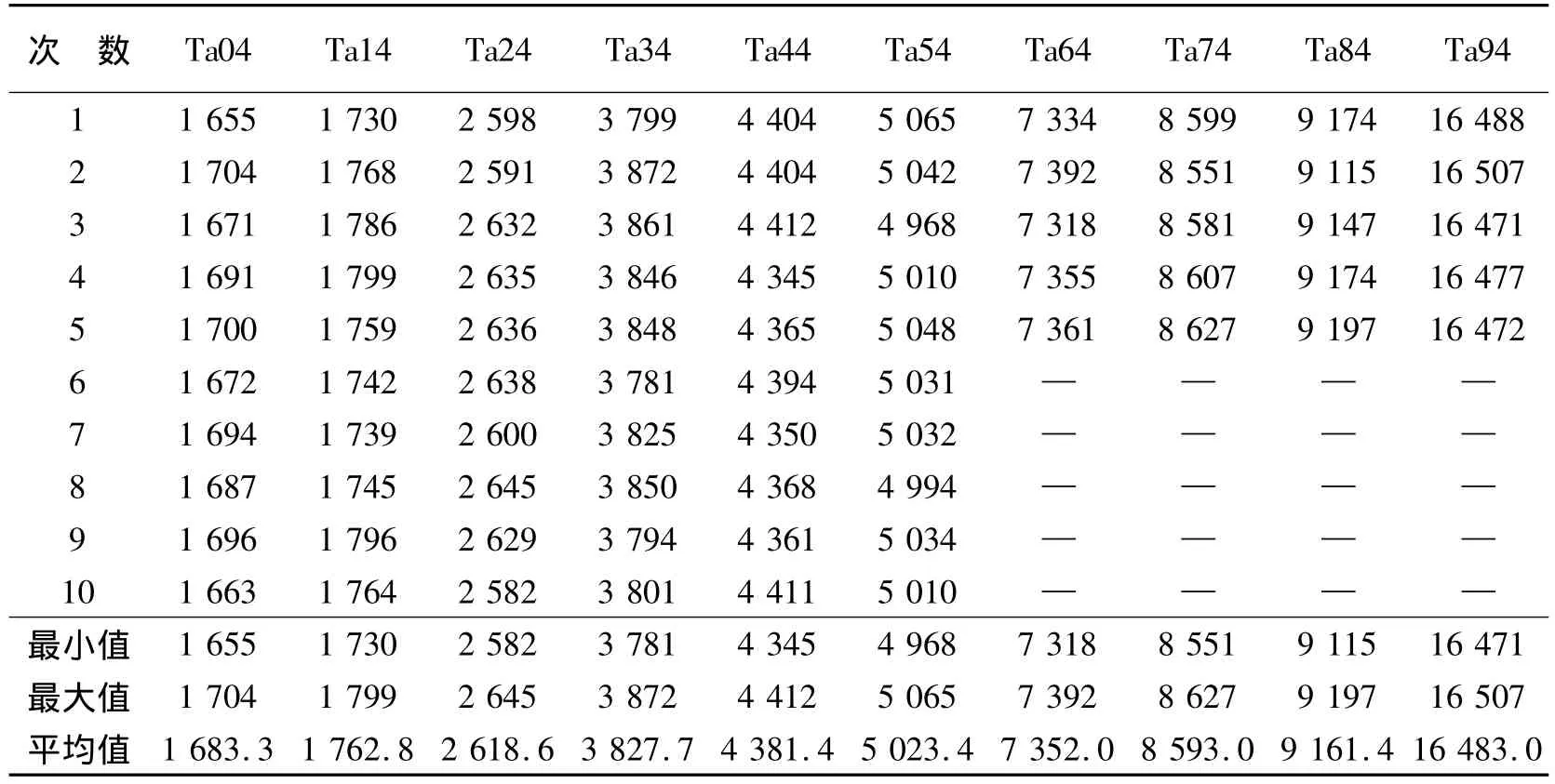
表4 萤火虫算法测试结果Table 4 The experiment results of firefly algorithm

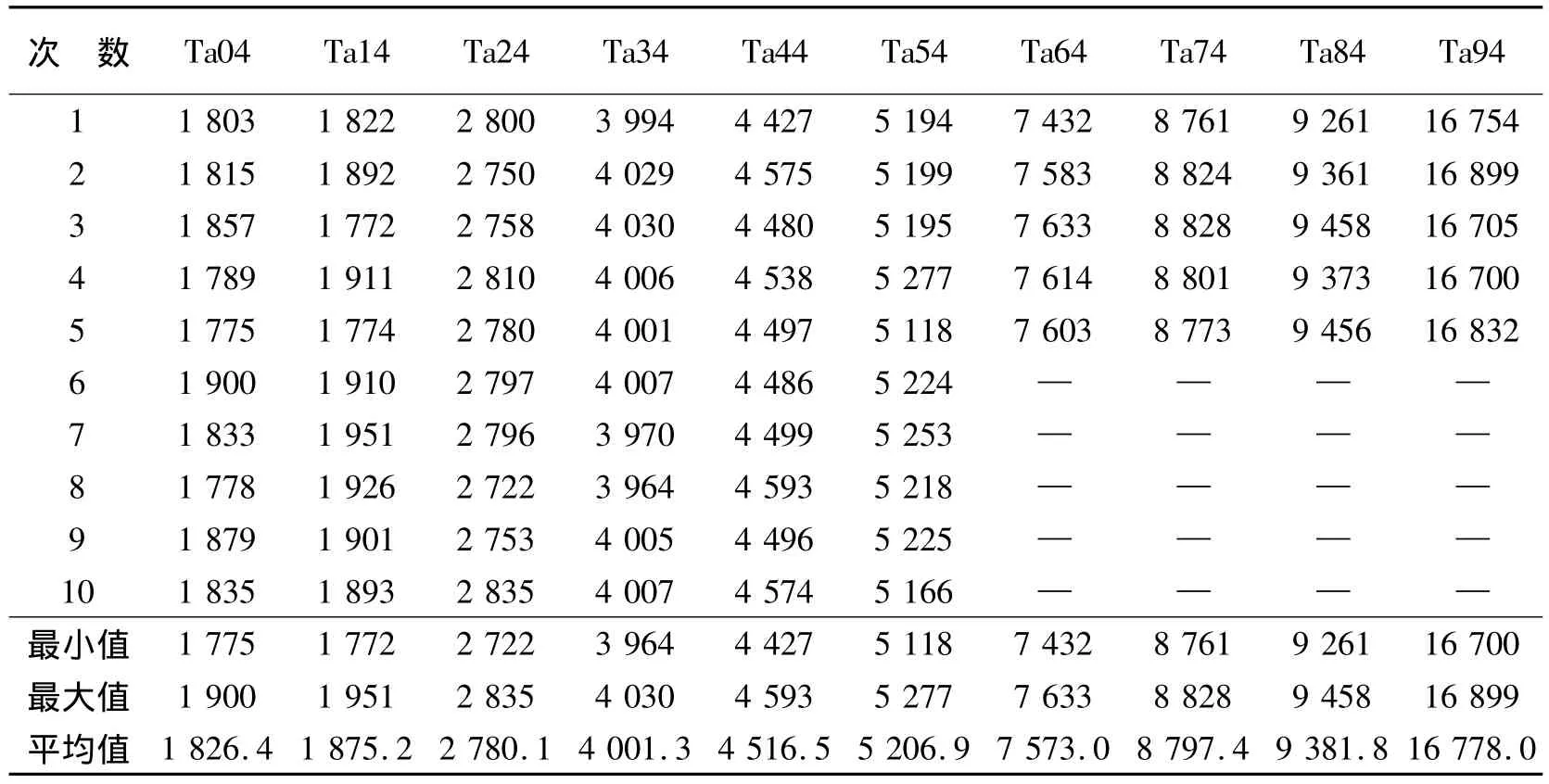
表5 粒子群算法求解结果Table 5 The experiment results of particle swarm algorithm

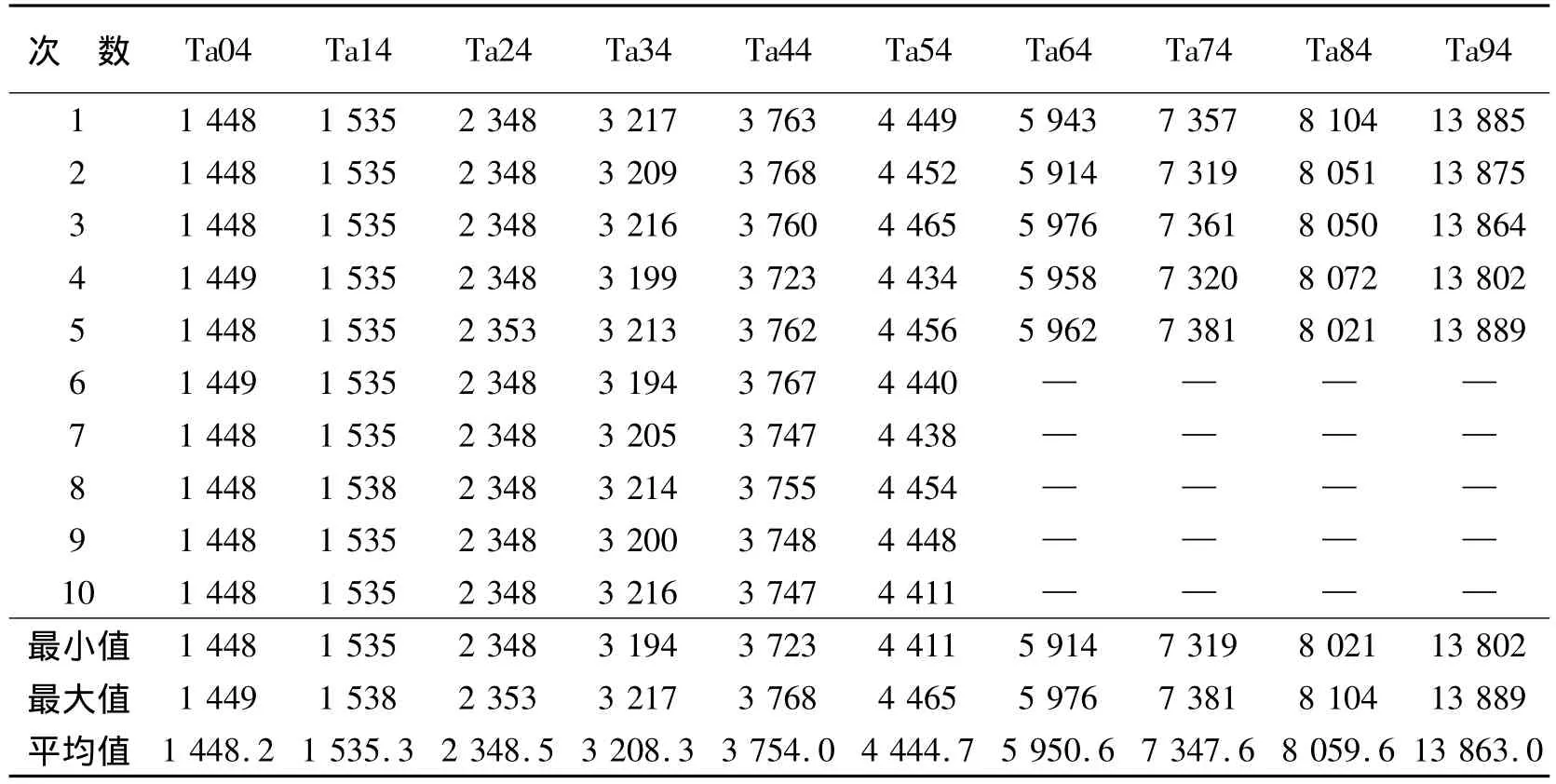
表6 改进的萤火虫算法求解结果Table 6 The experiment results of improved firefly algorithm

5 结束语

本文提出了一种改进的萤火虫算法，设计了双重初始化方法，引入了NEH启发式方法，重新设计了算法中个体位置的更新方式，并引入了莱维飞行来增大种群的搜索域.在求解阻塞流水线调度问题时，设计了一种将实数编码离散化的机制，实现了实数编码算法对离散化问题的求解.此外，本文还引入了一种局部搜索算法来加强算法的局部搜索能力.实验结果表明，改进后的萤火虫算法在求解阻塞流水线调度问题时，性能有了明显提高，而且随着问题规模的增大，这种提高更加明显，体现了算法的有效性和鲁棒性.

由于阻塞流水线调度问题具有很重要的实际应用价值，因此将来的工作会考虑把其他优秀的算法引入到这个问题中进行求解.另外，由于元启发式算法普遍存在计算量大的问题，将来的工作还应该考虑如何提高求解效率.

［1］ALLAHYERDI A，NG C T，CHENG T C E，et al.A survey of scheduling problems with setup times or costs［J］.European Journal of Operational Research，2008，187(3):985-1032.

［2］MCCORMICK S T，PINEDO M L，SHENKER S，et al.Sequencing in an assembly line with blocking to minimize cycle time［J］.Operations Research，1989，37(6):925-935.

［3］RONCONI D P.A note on constructive heuristics for the flowshop problem with blocking［J］.International Journal of Production Economics，2004，87(1):39-48.

［4］CARAFFA V，IANES S，BAGCHI T P，et al.Minimizing makespan in a blocking flowshop using genetic algorithms［J］.International Journal of Production Economics，2001，70(2):101-115.

［5］RONCONI D P.A branch-and-bound algorithm to minimize the makespan in a flowshop with blocking［J］.Annals of Operations Research，2005，138(1):53-65.

［6］GRABOWSKI J，PEMPERA J.The permutation flow shop problem with blocking.A tabu search approach［J］.Omega，2007，35(3):302-311.

［7］WANG Ling，PAN Quanke，SUGANTHAN P N，et al.A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems［J］.Computers ＆ Operations Research，2010，37(3):509-520.

［8］YANG Xinshe.Nature-inspired metaheuristic algorithms［M］.Frome，UK:Luniver Press，2008:81-96.

［9］YANG Xinshe.Firefly algorithms for multimodal optimization［C］//Proceedings of the 5th International Conference on Stochastic Algorithms:Foundations and Applications.Berlin/Heidelberg，Germany:Springer-Verlag，2009:169-178.

［10］NAWAZ M，ENSCORE E E J，HAM I.A heuristic algorithm for the m-machine，n-job flow shop sequencing problem［J］.Omega，1983，11(1):91-95.

［11］BROWN C T，LIEBOVITCH L S，GLENDON R.Lévy flights in Dobe Ju/＇hoansi foraging patterns［J］.Human Ecology，2007，35(1):129-138.

［12］PAVLYUKEVICH I.Lévy flights，non-local search and simulated annealing［J］.Journal of Computational Physics，2007，226(2):1830-1844.

［13］YANG Xinshe.Firefly algorithm，Lévy flights and global optimization［C］//Research and Development in Intelligent Systems XXVI.London，UK:Springer，2010:209-218.

［14］YANG Xinshe.Firefly algorithm，stochastic test functions and design optimization［J］.International Journal of Bio-Inspired Computation，2010，2(2):78-84.