采用遗传算法的多机自由飞行冲突解脱策略

吴君，张京娟

(北京航空航天大学仪器科学与光电工程学院，北京100191)

随着航空运输需求量的不断增长，空中交通面临着越来越严重的航线拥挤，给现有的交通管制系统带来前所未有的压力.在现行空中交通管制模式下［1-2］，民航飞机都是遵照地基导航系统所限定的由无线电信标建立起来的航线安排航班的，飞机必须沿着由一系列导航台组成的固定航路进行飞行.由于这些设施不是在任何地方都建立的，因而飞机不能选取通往目的地的最直接路线，这导致航路交通日益拥挤，空域整体利用率不高.对于这种状况，“自由飞行”是一个有效的解决办法.

然而，飞行数量的增加和自由飞行路线的多向性必然增加了飞行冲突的可能性.尤其是低空空域飞行流量密集，可用高度层有限，所以研究飞行冲突检测与解脱方法和技术的发展都至关重要，并且将是影响自由飞行能否实现的一项关键技术［3］.

遗传算法作为一种新的全局优化搜索算法［4］，以其简单通用、鲁棒性强、适合并行处理及应用范围广等显著特点，奠定了它作为21世纪关键智能计算之一的地位.国内应用遗传算法解决冲突解脱问题已经取得了一定的进展，但大多局限在研究两机情况和变航向的方法［5-6］.本文应用遗传算法解决了两机及多机间通过改变飞行速度和方向的冲突解脱问题.

1 基于遗传算法的冲突解脱算法

遗传算法是模拟生物在自然环境中的遗传和进化过程形成的一种全局优化概率搜索算法，它反复通过选择、交叉和变异等操作算子作用于整个进化群体，最终得到问题的最优解或近似最优解［7］.图1所示为遗传算法的基本流程图.

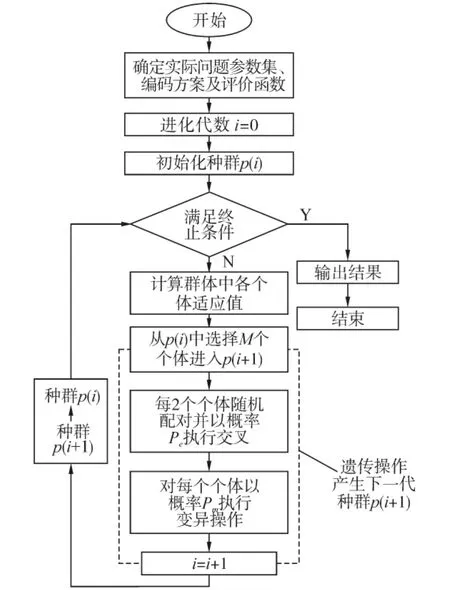
图1 遗传算法基本流程Fig.1 Basic flow chart of the genetic algorithm

1.1 模型简化

根据国家空管安全规定和实际飞行操控的具体情况，在研究过程中将对实际问题做如下简化.

1)飞机在飞行过程中，除了起飞和降落阶段，考虑到旅客的舒适和节约燃料，都是定高飞行，所以将问题简化为二维平面的冲突解脱问题.

2)考虑到飞机实际飞行过程中不会做太大角度的变航向飞行，假设飞机能选择的飞行航向改变范围为［－35°，35°］.为求得最优飞行路径，将此变化范围均匀地划分成若干份.

3)为了保证飞机按时到达目的地，假设飞机在所飞方向上的分速度不变，飞机偏航时偏航方向上的速度分量随偏航角度大小变化.

根据我国空管安全规定［8］，雷达管制条件下巡航阶段2架航班之间的间隔大于等于20 km时，不存在飞行冲突.那么在仿真分析区域内，算法中飞机以步长10 km的间隔前进.在任何时刻当2架飞机间的距离小于20 km时，即认为有冲突的可能，需要采取措施以避免冲突.

1.2 改变航向冲突解脱策略

1.2.1 改变航向冲突解脱算法方案

根据算法流程，具体实现途径如下.

1)编码方式.采用二进制编码，用6位二进制编码表示［－35°，35°］的偏航角，N 为飞机的数量，这样就需要6N位二进制数来表示偏航角.

2)目标函数和约束条件的确定.从燃料消耗角度看，希望飞机在不发生冲突的情况下沿最短路径飞行，即

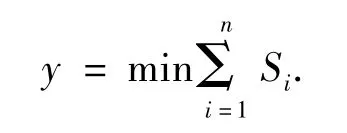
式中:Si为一架飞机从进入区域到离开区域的总飞行距离.

同时，应该保证区域内的所有飞机间的距离满足国家空管安全规定，即

式中:(xi，xj)、(yi，yj)为区域内任意2架飞机的坐标.

对于不满足安全距离的飞行路径，采用惩罚函数的方法使其不易进入下一代的计算中，即

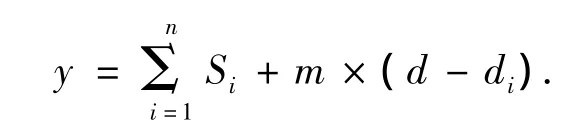
式中:∑Si为飞机的飞行路径长度，m为比例系数，d－di为2架飞机间最小安全距离与实际距离的差值.这样不满足最小安全距离的飞行路径总飞行长度比满足最小安全距离的总飞行长度大，在以后的选择过程中就不易被选中.

3)选择采用随机遍历选择法［9］，如图2所示，设NV为需要选择的个体数目，等距离地选择个体，选择指针的距离是1/NV，第1个指针的位置由［0，1/NV］的均匀随机数决定.

图2 随机遍历选择法Fig.2 Stochastic universal sampling method

这样，通过计算各个体的适应值，飞行距离短的个体具有较大的适应值，在图2的轴上占有距离较长，更容易被选中进入下一代计算.

4)交叉和变异.采用单点交叉算子，即在个体编码串中只随机设置一个交叉点，然后在该点相互交换部分基因.采用离散变异算子，用特定概率(变异率取为0.02)对当前种群中某个元素进行变异，也就改变飞机在这点的偏航角度.

5)遗传算法的终止.设定遗传算法运行代数为1 000代，并且设定如果连续30代运算结果变化范围小于0.000 001，则算法结束.如果1 000代内没有符合条件的结果则算法也相应停止，需要进行一些参数调整或重新启动.

1.2.2 仿真及结果

仿真参数设置如下:2架飞机一架自西向东飞行，另一架飞机自南向北飞行;飞行距离为90 km，两机间的安全距离为20 km;代沟为0.7，即在每次的选择过程中将父代中70%的较优个体遗传到下一代，变异率0.02，交叉率0.7;种群规模设置为600，最大迭代次数为1 000次，同时当连续相邻30代种群变化幅度小于0.000 001时，即认为此时的解为近似最优解，算法终止.图3给出了一次遗传算法的仿真过程.可以看出，生成的初始种群包含了设置的整个算法空间，保证了初始种群的多样性.随着算法的进行，那些偏离最优解较大的个体已经被淘汰掉，保留下来的个体均为距最优解较近的个体.算法在第214代得出了最优解，2条飞行路径不仅不存在冲突情况，也保证了最短飞行距离.

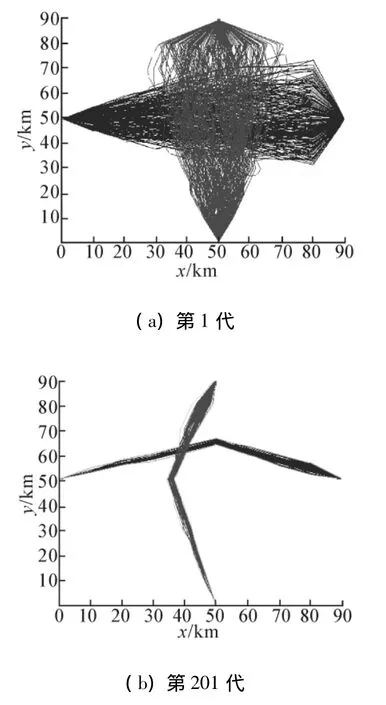
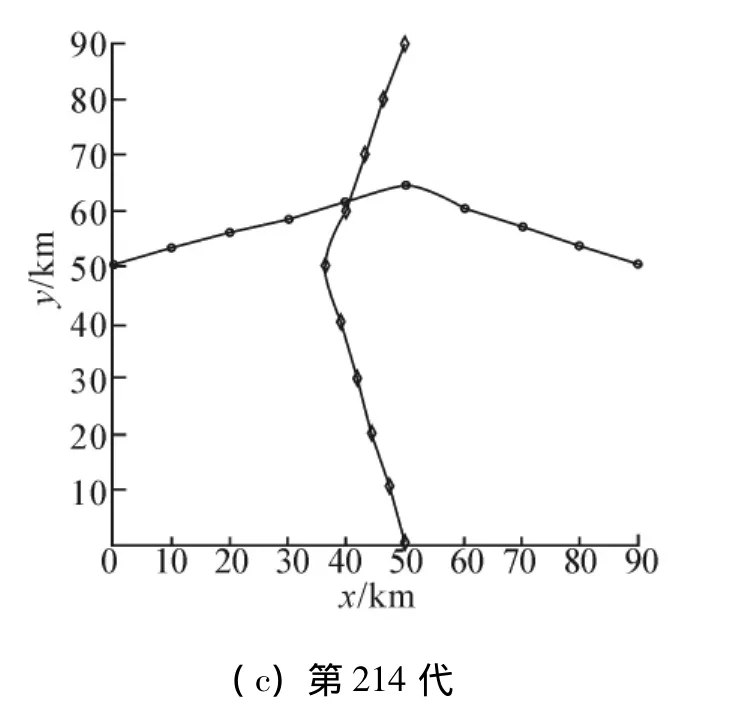
图3 2机冲突解脱仿真过程Fig.3 The diagrams of 2 airplanes procedure

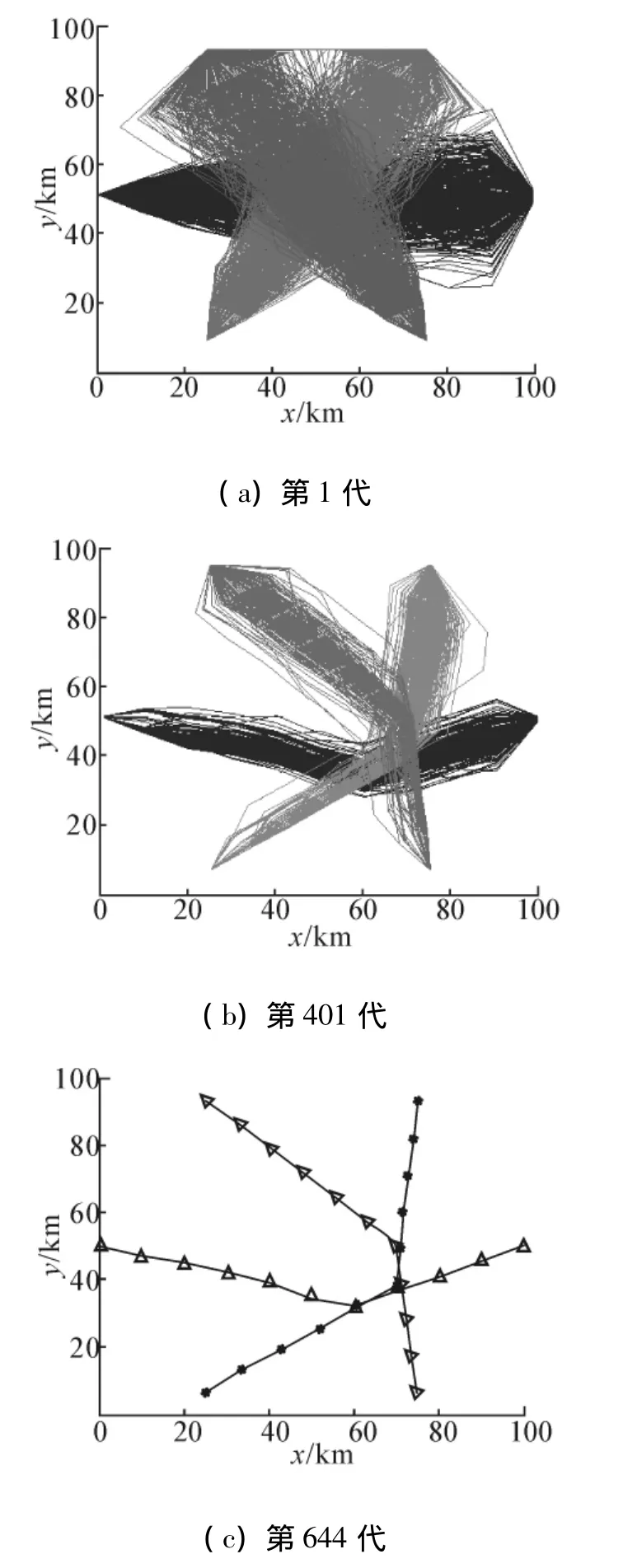
图4 3机冲突解脱仿真过程Fig.4 The diagrams of 3 airplanes procedure

为考察算法性能，给出三机冲突解脱的相关实验结果，如图4所示.可以看出初始种群仍能保证算法的多样性，且算法收敛性较好，最终可以收敛到一个最优解.

再通过观察图5所示六机冲突解脱的相关结果，发现在改变航向的冲突解脱算法中，各飞机都朝着各自相同方向改变，如果面临冲突问题的飞机架次较少时还可以通过协商改变航方向进行解脱，但是当架次较多时再临时协调解脱方案就会引起很大的混乱.因此在今后的冲突解脱规则中建立起相应“左行”或者“右行”机制的空中“交通规则”，规范面临冲突问题时飞机的解脱方案将会给实际冲突解脱问题带来极大的便利，这对今后实际飞行具有一定参考意义.

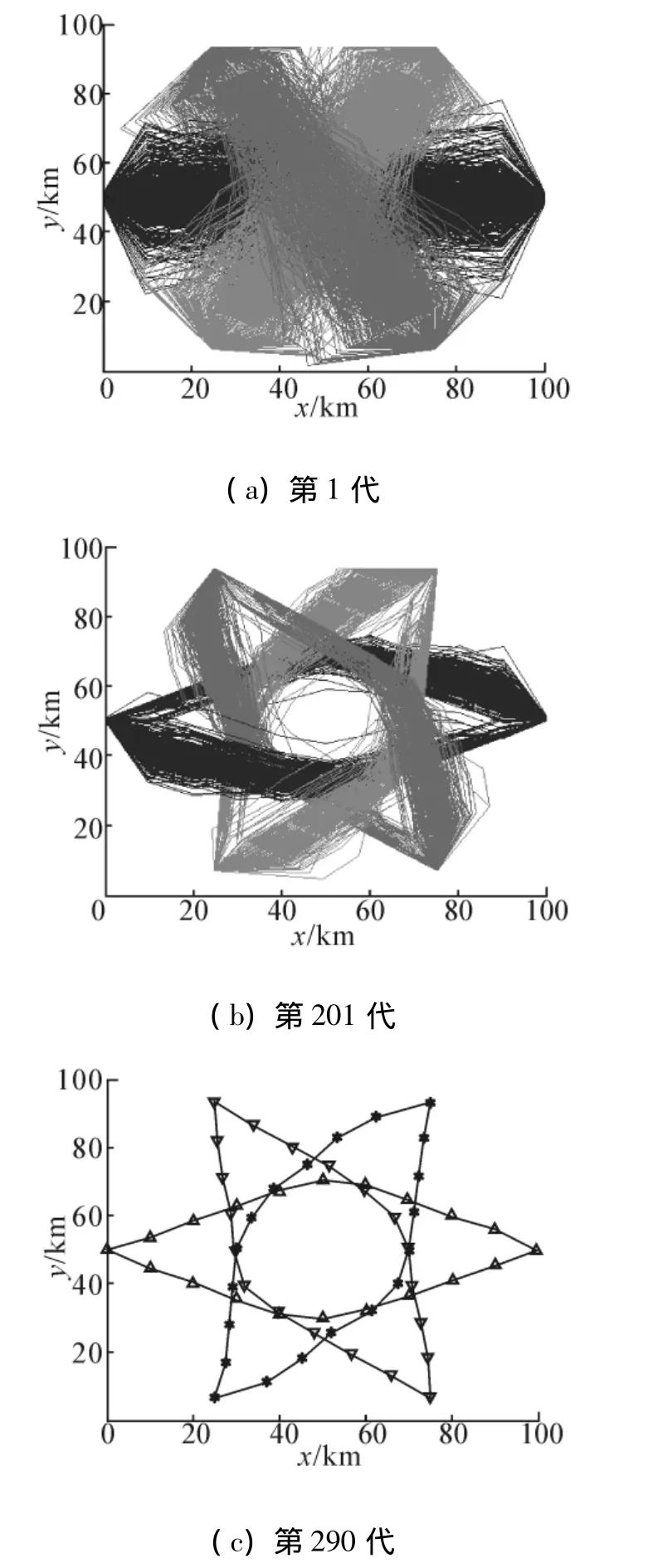
图5 六机冲突解脱仿真过程Fig.5 The diagrams of 3 airplanes procedure

1.3 改变速度冲突解脱策略

1.3.1 改变速度冲突解脱算法方案

上述算法模型是当有潜在飞行冲突时，执行改变飞行航向的策略取得的结果，为了提供更加充实的理论参考，下面研究采用改变飞行速度策略的情况.

根据我国空管安全规定和实际飞行情况，对实际情况做如下简化.

1)仍然将问题简化为二维平面的飞行冲突解脱问题.

2)为了保证飞机按照规定时间到达目的地，不会因为加速飞行而提前到达，也不会因为降低速度而推迟到达时间，假设飞机在整个飞行过程中既有加速过程也有减速过程.

3)考虑到飞机实际飞行过程中不能太大地改变飞行速度，假设飞机的飞行速度变化范围为加速或减速为正常飞行速度的50%，即可以将正常飞行速度的50%～150%的范围划分为若干份.

4)仍假设飞机以步长为10 km，在任何时刻当2架飞机间的距离小于20 km时，即认为有冲突的可能，需要调整速度来避免冲突.

算法流程和改变航向策略相似，具体实现途径如下.

1)选择编码方式.采用二进制编码，用6位二进制编码表示正常飞行速度的50%～150%的速度变化，N为飞机的数量，这样就需要6N位二进制数来表示速度变化大小.

2)目标函数的确定.从燃料消耗角度和旅客舒适度来看，总是希望飞机在不发生冲突的情况下尽可能少地变速，即

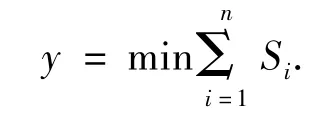
式中:Si为飞机当前时刻位置和不变速时理论位置之间的距离.

3)其余条件和改变航向策略相同.

1.3.2 仿真及结果

图6为算法一次执行结束时得出的最优解，可以看出算法在第308代收敛得出了最优解，自西向东的飞机先减速再加速，而自南向北的飞机先加速再减速，2架飞机通过改变飞行速度不仅避免了相互间的冲突情况，也保证了总体的最优飞行路线.

图7为算法一次运行结束时得出的最优解，可以看出在第518代时收敛，自西向东的飞机先加速再减速，而自东南向西北的飞机先减速再加速，自西南向东北飞行的飞机速度变化较小.然而发现一个问题就是仅靠改变速度策略对于两机冲突具有较好的解脱效果，无外乎其中一架飞机加速另一架飞机减速，这很好理解.但是当3架飞机冲突时就发现一架飞机加速一架飞机减速，另一架飞机要么超前要么略晚点到达.本仿真中自西南向东北飞行的飞机就是提前1个时刻到达了目的地.要不然速度改变量的幅度大一些，才能确保另一架飞机也能按时到达.

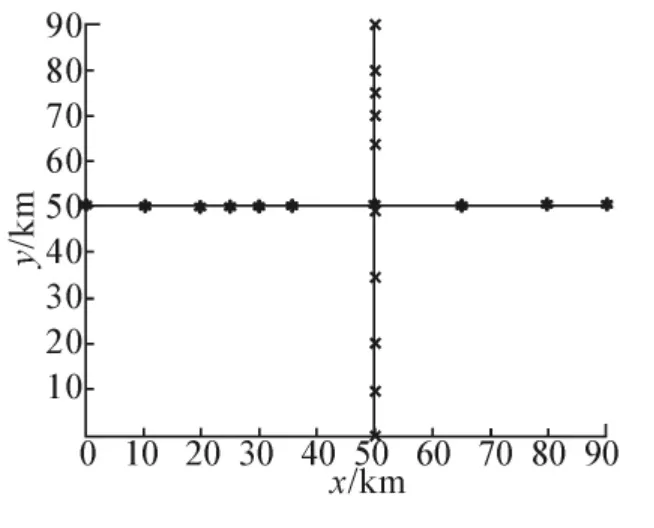
图6 第308代Fig.6 The 308th generation

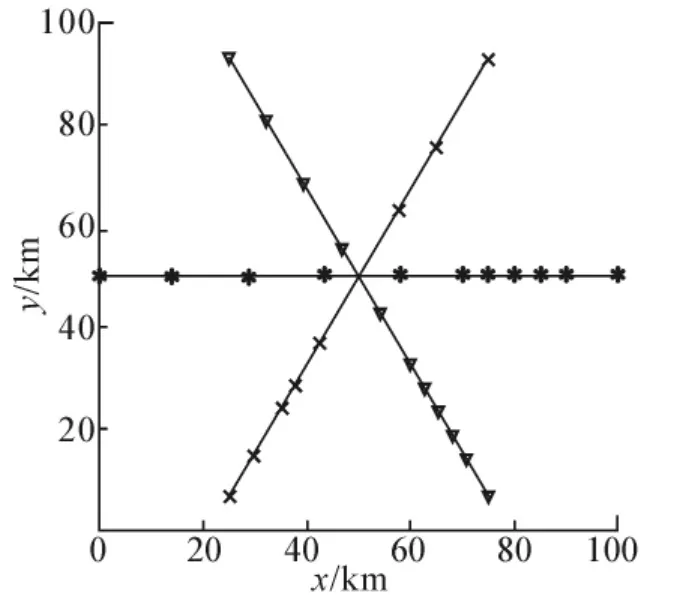
图7 第518代Fig.7 The 518th generation

上述实验结果表明，所设计的算法具有较好的性能，无论是改变航向策略还是改变速度策略，对于两机和三机冲突解脱，算法都有着良好的表现.

2 结束语

本文基于遗传算法的冲突解脱问题进行了深入研究，在研究两机冲突解脱的基础上进一步研究了多机的冲突解脱方法，通过大量的仿真，验证了所提出的改变飞行航向和飞行速度的策略都可以实现有效冲突解脱.通过仿真结果也可以看出，采用改变速度的解脱策略在处理多机冲突问题时具有一定的局限性，而采用改变航向的方法具有更好的适用性，同时还讨论了多机冲突解脱时相应的飞行机制问题.这些结果为自由飞行和空管自动化系统的研究提供了重要的理论参考.另外，文中仅对2种解脱方法分别进行了研究，并未讨论这2种方法结合的解脱策略，这有待进一步研究.

［1］张军.现代空中交通管理［M］.北京:北京航空航天大学出版社，2003:17-33.

［2］程丽媛.自由飞行冲突探测与解脱技术的国内外发展和研究现状［J］.中国民航飞行学院学报，2007，39(5):21-23.CHENG Liyuan.The development and research of free flight conflict detection and resolution technology at home and abroad［J］.Journal of Civil Aviation Flight University of China，2007，39(5):21-23.

［3］KUCHAR J K，YANG L C.A review of conflict detection and resolution modeling methods［J］.IEEE Transactions on Intelligent Transportation Systems，2000，1(4):179-189.

［4］周明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999:2-3.

［5］杨尚文，戴福青.基于一种免疫遗传算法的自由飞行冲突解脱［J］.航空计算技术，2007，37(1):41-43.YANG Shangwen，DAI Fuqing.Conflict resolution in free flight based on an immune genetic algorithm［J］.Aeronautical Computing Technique，2007，37(1):41-43.

［6］刘星，胡明华，董襄宁.遗传算法在飞行冲突探测解脱中的应用［J］.南京航空航天大学学报，2002，34(1):36-39.LIU Xing，HU Minghua，DONG Xiangning.Application of genetic algorithms for solving flight conflicts［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2002，34(1):36-39.

［7］赵荣，张京娟.改进的遗传算法在飞行冲突解脱中的应用［J］.电子测量技术，2009，32(11):37-39.ZHAO Rong，ZHANG Jingjuan.Conflict resolution based on an improved genetic algorithm［J］.Electronic Measurement Technology，2009，32(11):37-39.

［8］王洁宁，袁志娟.基于粒子群算法的飞行冲突解脱问题［J］.中国民航大学学报，2010，28(4):1-4.WANG Jiening，YUAN Zhijuan.Study on resolution of flight conflicts based on particle swarm optimization［J］.Journal of Civil Aviation University of China，2010，28(4):1-4.

［9］魏全新，刘贤锋，黄锵，等.遗传算法选择方法的比较分析［J］.通讯和计算机，2008，5(8):61-65.WEI Quanxin，LIU Xianfeng，HUANG Qiang，et al.The comparison of different selection methods in genetic algorithms［J］.Journal of Communication and Computer，2008，5(8):61-65.