基于单频星载GPS数据的低轨卫星精密定轨

郭向 张强 赵齐乐 郭靖

（1武汉大学测绘学院，武汉430079）（2武汉大学卫星导航定位技术研究中心，武汉430079）

1 引言

由于对地观测卫星科学任务不同，因此其对轨道精度要求也不尽相同。一些重力卫星如CHAMP、GRACE、GOCE等，由于轨道精度要达到厘米级，因此其星上均搭载有高性能的双频GPS接收机；而有些卫星如QuickBird、KOMPSAT-1等对轨道精度要求并不太苛刻，其星上搭载的均为单频GPS接收机，这一方面可以节约成本、降低功耗，另一方面由于观测数据量显著减少因而可大大减轻数据下传的压力。对于利用星载双频GPS数据进行精密定轨，国内外学者已做了很多有益的探索并已实现厘米级的定轨精度。而对于利用星载单频GPS数据进行精密定轨的研究相对较少［1-3］。而国内的胡国荣等最早仅利用TOPEX／POSEIDON卫星P1码观测值采用几何法定轨并获得三维20m的定轨精度［4］；彭冬菊等仅利用C／A码观测值，为消除电离层延迟的影响，定轨中同时估计电离层比例因子并获得了三维2dm的定轨精度［5］。为了深化单频定轨的研究，同时为了展示HY-2A卫星和ZY-3卫星的单频定轨性能，本文利用HY-2A卫星和ZY-3卫星的星载单频GPS实测数据采用两种不同方案确定其简化动力学轨道，并通过观测值残差分析、与双频精密轨道比较、激光测卫检核等手段对所得轨道精度进行评估。

2 数据处理策略

星载单频与双频GPS数据处理的主要区别之一在于电离层延迟的改正。Garcia-Fernandez、Montenbruck等对CHAMP的星载GPS实测数据分析表明，其观测值受电离层延迟影响可达10m［6］，因此在数据处理中必须充分消除电离层延迟的影响。对于双频定轨通常采用无电离层延迟组合（LC／PC）来消除电离层延迟的影响，而对于单频定轨，一般采用半和改正组合进行电离层延迟改正。L1频率载波相位观测值、码观测值和半和改正组合观测值的观测方程分别为

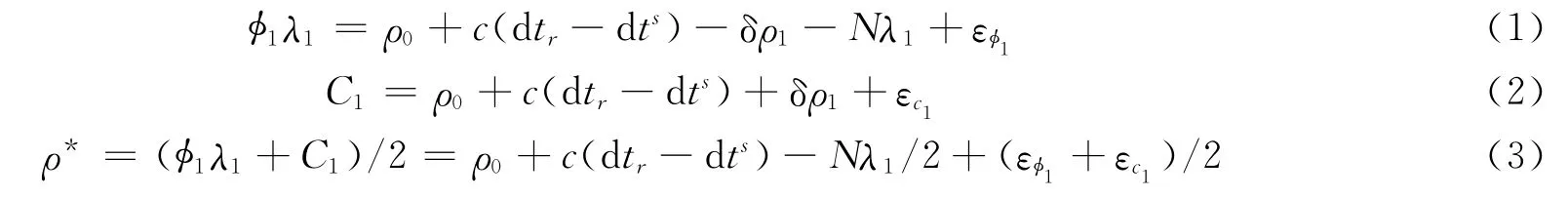
式中φ1、C1分别为L1频率上的载波相位和C／A码观测值；N为L1载波整周模糊度；λ1为L1载波波长；dtr、dts分别为接收机钟差和GPS卫星钟差；c为光速；δρ1为L1频率上电离层一阶项延迟改正量；εφ1、εc1分别为载波和码的多路径误差及观测噪声；ρ＊为半和改正组合观测值。

可以看出，同一频率上的载波相位和码观测值的电离层延迟一阶项改正量大小相等但符号相反，半和改正组合观测值通过对同一频率上的载波相位和码观测值求均值，消除了电离层延迟一阶项的影响［7］。此外，由于电离层延迟二阶项以上的影响通常只有毫米到厘米级［8］，因此在本文的研究中被忽略不计。

由于载波观测值噪声以及多路径误差相对于码观测值可忽略不计，因此半和改正组合观测值主要受码噪声及码多路径效应的影响。由公式（4）可以看出，该组合观测值噪声约为独立码观测值的一半，因此，高精度的码观测值将是决定单频定轨精度的关键因素，半和改正组合观测值噪声为

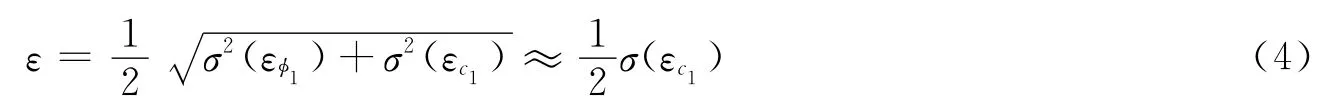
文献［3］的研究表明，采用半和改正组合消除电离层延迟的影响可取得最高的定轨精度，而在国内的单频定轨研究中尚未涉及该组合的应用。其原因之一在于对单频数据尚无较为有效的周跳探测方法。由公式（1）、（2）可以看出，单频数据中包含电离层延迟的影响，再加上低轨卫星的高动态性导致电离层延迟变化很快，因此一般的周跳探测方法不能很好地解决星载单频GPS数据的周跳探测问题。本文在数据预处理时采用单频码相组合法：

由式（5）可知，该组合不受星载接收机及GPS卫星几何位置的影响，也消除了接收机钟差及GPS卫星钟差的影响，仅受电离层延迟以及多路径效应和观测噪声的影响。由于码观测值多路径效应及观测噪声水平比载波相位要高很多，再加上低轨卫星的高动态性导致站星视线方向上的电离层延迟变化很快，因此该方法只能探测出大周跳［9］。而对于数据预处理中未探测出的小周跳，则采用事后残差编辑的方式来探测。

本文将采用两种数据处理方案：方案1直接使用载波和码原始观测值，不进行电离层延迟改正，观测值为L1＋C／A；方案2采用半和改正组合作为观测值来消除电离层延迟一阶项影响，观测值为半和改正组合观测值＋C／A。

本文利用武汉大学导航定位技术研究中心自主研发的导航与定位数据分析软件（PANDA软件）进行数据处理，具体策略见表1～表3所示。

表1 观测模型Tab.1 Measurement models

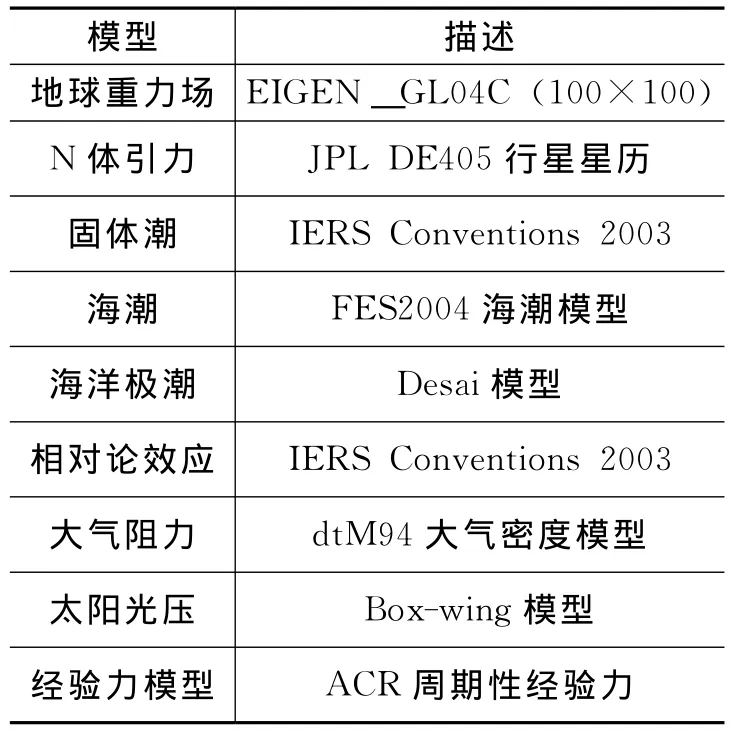
表2 力学模型Tab.2 Force models

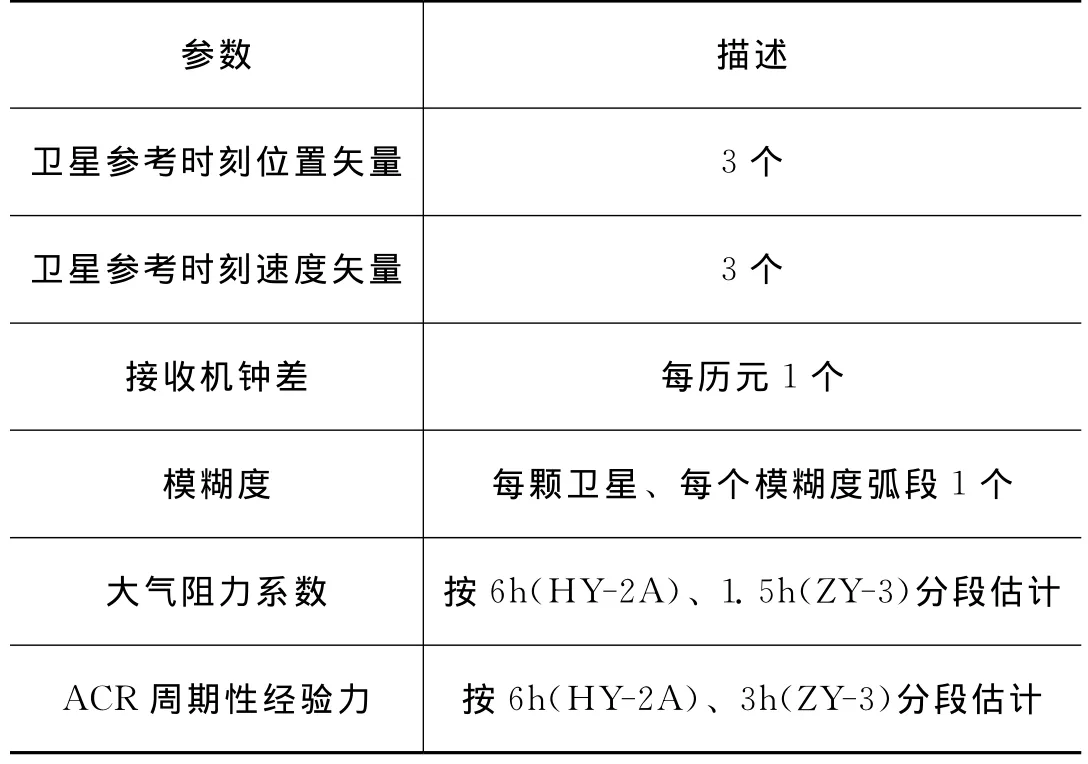
表3 待估参数Tab.3 Estimated parameters

3 定轨精度分析

基于上文所述的数据处理策略，本文解算了HY-2A卫星及ZY-3卫星2012年年积日37～51天的简化动力学轨道，下文将通过观测值残差分析、与双频精密轨道比较、激光测卫数据检核等方法来评估定轨精度。

3.1 观测值残差分析

图1为2012年37～51天方案2简化动力学定轨半和改正组合观测值及C／A码观测值验后残差均方根误差（Root Mean Square，RMS）序列图。从图1（a）可以看出，ZY-3卫星和HY-2A卫星半和改正组合观测值验后残差均方根误差均稳定在（0.21±0.01）m的范围内，表明二者的C／A码观测值精度约为0.4～0.5m，不过ZY-3卫星C／A码精度稍逊于HY-2A卫星。定轨中同时把C／A码当作独立观测值来使用，从图1（b）可看出二者RMS值稳定在1.9～2.3m范围内，这明显低于C／A码的观测精度。笔者认为有以下几个方面的原因：一是C／A码观测值中包含有未被消除的电离层延迟项，最终残留在观测值残差中；二是观测值中包含多路径误差的影响；三是未考虑码间偏差的影响，由于定轨中所采用的GPS卫星钟差是通过LC／PC组合解算，对C／A码并不适用，而对半和改正组合观测值来说，这部分误差会被模糊度参数吸收，因此在定轨中未予以考虑。虽然独立C／A码观测值误差较大，但考虑到其在定轨中的权重相对于半和改正组合观测值很小，因此对定轨结果影响可忽略不计。

图2所示为2012年第37天方案2简化动力学定轨半和改正组合观测值残差随方位角和高度角的分布图（其他天与该天相似）。图2取接收机天线坐标系为坐标参考系，其＋X方向为卫星飞行方向，同时也是方位角的起算方向，＋Y方向为星固系＋Y方向 （方位角为90°），＋Z方向为星固系的-Z方向。可以看出，半和改正组合观测值残差大都分布在±0.5m的范围内。而在低高度角处（＜30°），由于观测信号衰减较为严重且受多路径效应影响较大，从而导致观测值残差较大，这一现象在飞行后半球表现尤为明显 （方位角90°～270°）。另外可以看出，在低高度角处，飞行后半球的观测值明显多于飞行前半球，这可能是由于接收机接收信号需要达到一定的信号强度或载噪比量值，而高度角处比较容易满足这一条件，之后会保持连续跟踪观测，因而在跟踪GPS卫星初始阶段观测数据较少。

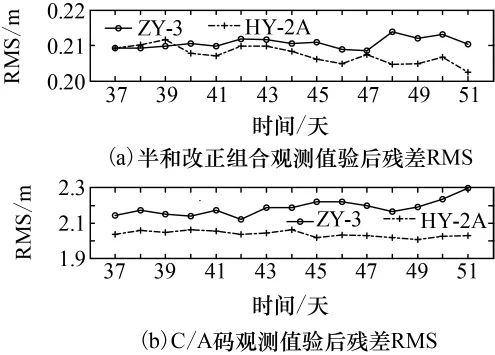
图1 方案2观测值验后残差RMSFig.1 RMS of observation residuals for solution 2

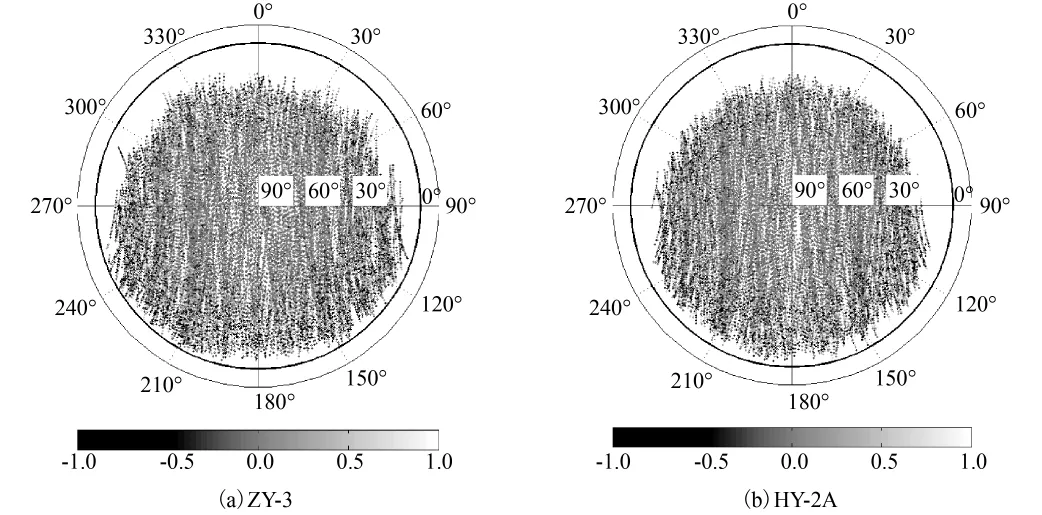
图2 2012年第37天方案2半和改正组合观测值验后残差天空图Fig.2 Sky plots of GRAPHIC residuals for solution 2for day 37of 2012

3.2 与双频轨道比较

武汉大学承担了HY-2A卫星联合GPS和SLR精密定轨的任务，郭靖等基于PANDA软件利用HY-2A星载双频GPS数据确定了其精密轨道，经过激光测卫数据检核、与法国国家空间局确定的精密轨道比较等方法表明，其精度为2～3cm［10］。笔者采用文献［6］中的数据处理方法确定了HY-2A卫星和ZY-3卫星的精密轨道并作为本文研究的参考轨道。

表4所示为方案1、方案2所解算的单频轨道与双频轨道互差RMS统计结果。可以看出，由于HY-2A卫星轨高约为970km，而电离层主要分布在90～1000km的范围内，因此其观测值受电离层延迟影响较小，即使在不考虑电离层延迟影响的情况下，也能获得较高的定轨精度；而ZY-3卫星轨高约为505km，其观测值受电离层延迟影响较大，因此在不进行电离层延迟改正的情况下，其定轨精度明显低于HY-2A卫星。通过对比方案1和方案2可以发现，方案2中采用半和改正组合消除电离层延迟的一阶项影响后，定轨精度相对于方案1有显著提高，并且以轨道径向精度改善最为明显，其中ZY-3卫星径向精度提高约89.6%，HY-2A卫星提高约64.4%，说明电离层延迟对轨道径向影响较大，因此消除电离层延迟影响后，轨道径向精度有明显提高。

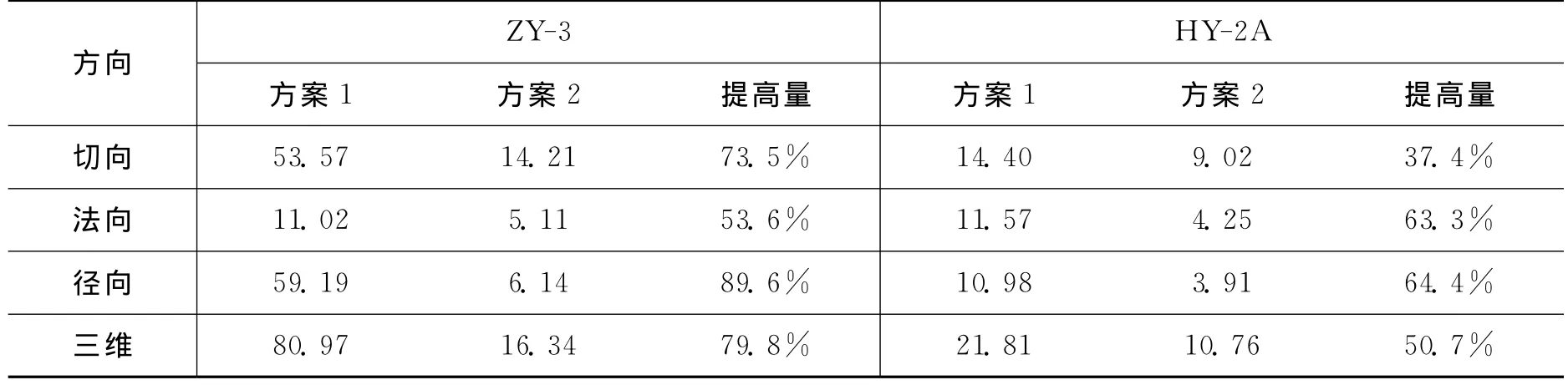
表4 不同单频轨道解与双频轨道解互差RMS［cm］及方案2相对于方案1轨道精度提高量Tab.4 RMS ［cm］of the orbit differences with respect to DF reference orbit for different SF orbit solutions and improvement with respect to solution 1for solution 2

3.3 激光测卫检核

利用激光测卫数据对轨道进行外部检核是轨道精度评估最有效的方式之一。由于在本文处理时段内没有发布ZY-3卫星的激光测卫数据，因此这里只对HY-2A卫星的单频轨道进行检核。本文采 用 Riga、Graz、Postdam、 Wettzell、Changchun、Katzively、Herstmonce、Zimmerwald、San Fernan、Mount Stro、San Juan、Grasse、Matera、Shanghai等14个SLR测站的观测数据对方案1和方案2的单频轨道进行外部检验。统计结果如图3、图4所示。

图3、图4分别为对方案1和方案2所确定的HY-2A卫星单频轨道进行SLR检核时的先验残差（RES）序列图及其单天先验残差均方根误差（RMS）统计图，对比二图可以看出，方案2中采用半和改正组合消除电离层的一阶项影响后，SLR检核先验残差均值和RMS均显著减小。由图4（a）可以看出方案2中所有残差均分布在±20cm的范围内，而所有残差的均值为0.01cm，说明定轨中不存在系统性误差；从图4（b）可以看出所有弧段的RMS均小于1dm，而整体RMS为5.24cm。由于SLR检核RMS主要反映轨道误差在站星方向投影分量的大小，因此其三维误差约为该值的2倍［11］，这与表4所示结果是一致的。

图3 方案1HY-2A卫星单频轨道SLR检核Fig.3 SLR validation for HY-2A simple-frequency orbit for solution 1

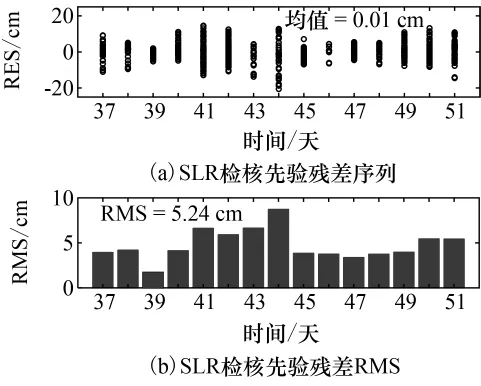
图4 方案2HY-2A卫星单频轨道SLR检核Fig.4 SLR validation for HY-2A simple-frequency orbit for solution 2

4 结束语

本文利用单频码相组合法解决了单频星载GPS数据的周跳探测问题，并采用半和改正组合观测值确定了高精度的卫星轨道，其中HY-2A卫星三维精度达到1dm左右，ZY-3卫星为1～2dm，二者径向精度均优于1dm。本文的研究成果表明对于搭载单频GPS接收机的低轨卫星，采用半和改正组合是一种非常有效的定轨手段并可实现厘米级定轨。同时，本文的相关成果对于我国后续搭载单频GPS接收机的卫星计划具有一定的参考价值。

［1］MONTENBRUCK OLIVER.Kinematic GPS positioning of LEO satellites using ionosphere-free single frequency measurements［J］.Areospace Science and Technology，2003，7（5）：396-405.

［2］MONTENBRUCK OLIVER，RAMOS-BOSCH PERE.Precision real-time navigation of LEO satellites using global positioning system measurements［J］.GPS Solutions，2008，12（3）：187-198.

［3］BOCK H，JÄGGI A，DACH R，et al.GPS single-frequency orbit determination for low Earth orbiting satellites［J］.Advances in Space Research，2009，43（5）：783-791.

［4］胡国荣，欧吉坤，崔伟宏.星载单频GPS接收机低轨卫星几何法定轨研究 ［J］.天文学报，2000，41（3）：278-288.HU GUORONG，OU JIKUN，CUI WEIHONG.A Research on Geometric Orbit Determination for GPS-based Single-frequency Receivers Aboard Low Earth Satellites［J］.Acta Astronomica Sinica，2000，41（3）：278-288.

［5］彭冬菊，吴斌.GIM在LEO卫星单频GPS定轨中的应用 ［J］.天文学报，2012，53（1）：36-50.PENG DONGJU，WU BIN.The Application of GIM in Precise Orbit Determination for LEO Satellites with Single-frequency GPS Measurements［J］.Acta Astronomica Sinica，2012，53（1）：36-50.

［6］GARCIA-FERNANDEZ M，MONTENBRUCK O.Low Earth orbit satellite navigation errors and vertical total electron content in single-frequency GPS tracking ［J］.Radio Science，2006，41（5）：1-7.

［7］TEUNISSEN P J G，KLEUSBERG A.GPS for Geodesy［M］.Germany：Springer Verlag，1996：128.

［8］HOQUE M，JAKOWSKI N.Higher order ionospheric effects in precise GNSS positioning ［J］.Journal of Geodesy，2007，81（4）：259-268.

［9］李征航，张小红.卫星导航定位新技术及高精度数据处理方法 ［M］.武汉：武汉大学出版社，2009：34.LI ZHENGHANG，ZHANG XIAOHONG.New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning［M］.Wuhan：Wuhan University Press，2009：34.

［10］郭靖，赵齐乐，李敏，等.利用星载GPS观测数据确定海洋2A卫星cm级精密轨道 ［J］.武汉大学学报（信息科学版），2013，38（1）：52-55.GUO JING，ZHAO QILE，LI MIN，et al.Centimeter Level Orbit Determination for HY-2AUsing GPS Data［J］.Geomatics and Information Science of Wuhan University，2013，38（1）：52-55.

［11］MONTENBRUCK OLIVER，SWATSCHINA PAUL，MARKGRAF MARKUS，et al.Precision spacecraft navigation using a low-cost GPS receiver［J］.GPS Solutions，2012，16（4）：519-529.