基于自适应联邦滤波的卫星姿态确定
2013-02-07李鹏唐健段广仁宋申民
李鹏 唐健 段广仁 宋申民
(1 湘潭大学信息工程学院智能计算与信息处理教育部重点实验室,湘潭411105)(2 哈尔滨工业大学航天学院,哈尔滨 150001)
1 引言
随着卫星智能自主控制技术的发展,对卫星姿态确定的精度和可靠性提出了越来越高的要求,仅仅依靠单一姿态敏感器提供的信息已经远远不能满足用户多方面的需求,因此多传感器系统的发展成为必然趋势。目前航天器主要利用惯性单元、红外地平仪、太阳敏感器和星敏感器进行定姿。联邦滤波是组合导航的主流算法,它根据信息分配原则保证了各子滤波器运算的独立和整体结果的最优。根据联邦滤波原理,将多敏感器的量测信息构成姿态确定信息融合系统,从而可解算出高精度姿态信息;同时,通过信息融合可以将多敏感器组合成高可靠性的智能容错姿态确定系统,实现故障诊断与系统重构,从而大大提高航天器的可靠性[1-2]。
联邦卡尔曼滤波器的子滤波器为卡尔曼滤波,采用常值噪声矩阵,无法反映各子系统量测噪声统计特性的变化,使得子系统估计误差变大,最终导致联邦卡尔曼滤波器出现估计误差变大,甚至滤波发散。本文提出在联邦卡尔曼滤波算法中采用模糊自适应卡尔曼滤波代替卡尔曼滤波,形成模糊自适应联邦滤波算法。最后将新算法运用到卫星多传感器姿态确定系统中,进行试验验证。
2 联邦卡尔曼滤波
联邦滤波算法采用信息分配原理来实现各个子滤波器的信息分享,各子滤波器并行运行,获得建立在子滤波器局部量测基础上的局部最优估计。这些局部最优估计在第二级滤波器即主滤波器内按融合算法合成,获得建立在所有量测基础的全局估计,全局估计再按照信息守恒原则反馈给各子滤波器[3]。联邦滤波器结构如图1所示[3]。
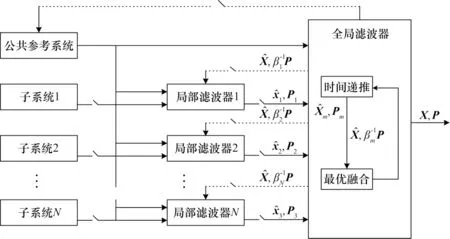
图1 联邦卡尔曼滤波Fig.1 Federated Kalman filtering
考虑两个子滤波器的模型:
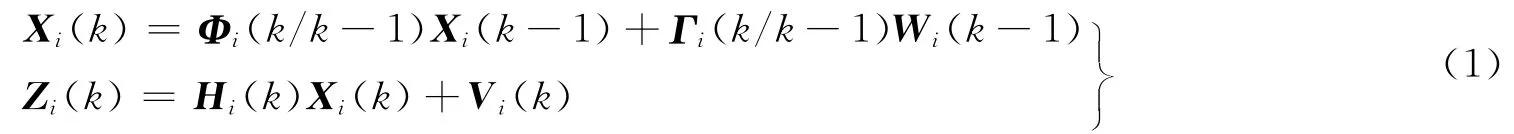
式中 Xi(k)为子系统i的状态变量;Zi(k)为第i个传感器的观测量;Wi(k)和Vi(k)分别为子系统i的系统噪声和量测噪声
联邦滤波器的设计步骤在文献[3]中已经有详细的说明,本文不再赘述。
3 可信度加权自适应联邦卡尔曼滤波
在联邦滤波算法中引入模糊自适应卡尔曼滤波代替卡尔曼滤波,形成模糊自适应联邦滤波算法,对各子系统量测噪声统计特性的变化进行检测、调整。模糊自适应卡尔曼滤波算法原理是应用模糊推理系统不断地调整量测噪声协方差阵的加权系数,使模型量测噪声逐渐逼近真实噪声水平[4]。
3.1 自适应卡尔曼滤波器
自适应卡尔曼滤波通过不断调整量测噪声协方差矩阵系数,使模型量测噪声逐渐逼近真实噪声。
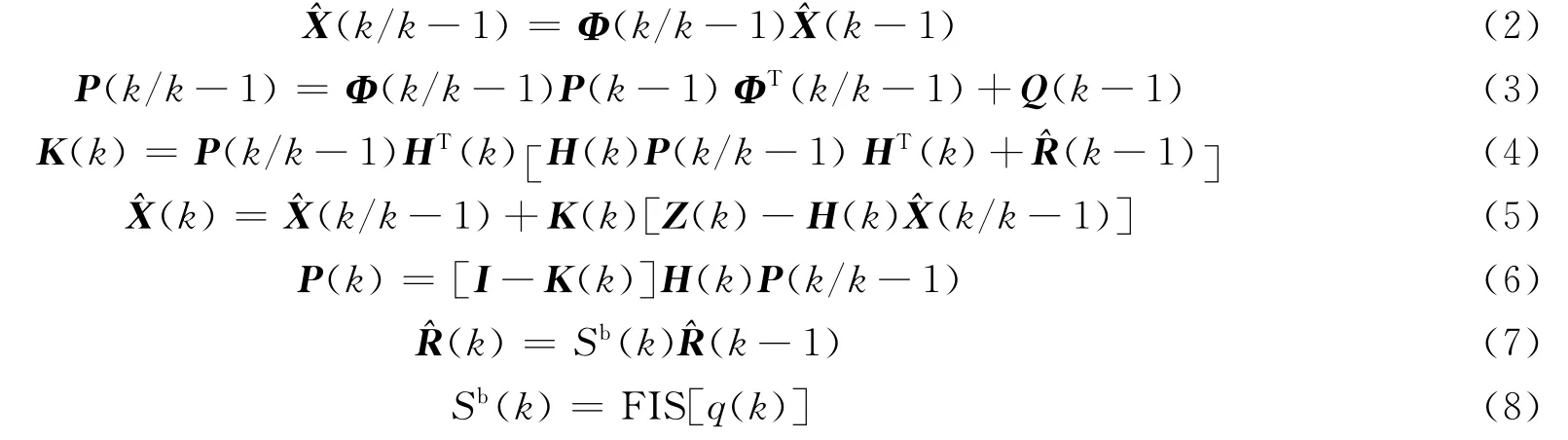
3.2 模糊推理计算S(k)
S(k)的取值由模糊推理系统FIS得到,系统输入为残差实测方差与理论方差的比值,残差方差的理论值Pr(k)为
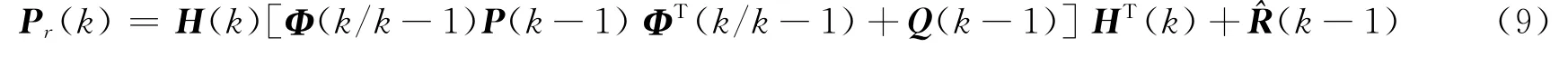
残差的实测方差Cr(k)为
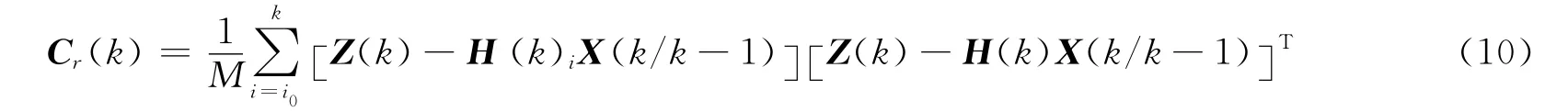
式中 Cr(k)为对最新的M 个残差向量方差求平均值;i0=k-M+1,M 由经验根据具体情况选定,主要起平滑作用。定义残差实测方差与理论方差的比值q(k)为

定义模糊子集equal表示在1附近,more表示基本大于1,less表示基本小于1,调整系数S(k)的模糊推理规则如下:若q(k)∈equal,那么S(k)∈equal;若q(k)∈more,那么S(k)∈more;若q(k)∈less,那么S(k)∈less。q(k)和S(k)的隶属度函数分别如图2、图3所示。选用中心法解模糊规则,此模糊推理系统为单输入单输出系统,只有三条模糊规则。
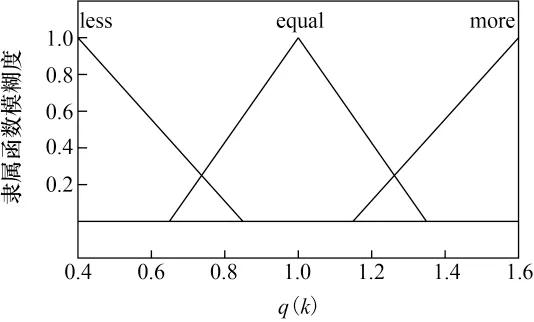
图2 q(k)的隶属度函数Fig.2 Membership function of q(k)
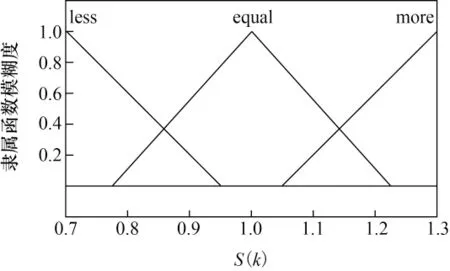
图3 S(k)的隶属度函数Fig.3 Membership function of S(k)
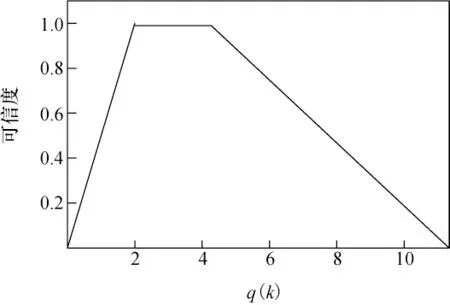
图4 q(k)的可信度Fig.4 Confidence level of q(k)
3.3 可信度加权自适应联邦滤波算法
不同的敏感器所获得的测量精度不同,为了保证高精度敏感器对融合后整体状态估计值影响大,同时隔离突发异常或故障的敏感器,提高融合后数据的可靠性和容错性,提出可信度加权自适应联邦滤波算法。各子滤波器输出状态及协方差估计值的同时输出残差比值,残差比值作为逻辑观测器的输入,由逻辑观测器计算子滤波器的可信度,然后用得到的可信度值对各子滤波器及联邦滤波器输出进行加权计算,得到全局数据融合[5-6]。子滤波器可信度函数采用如图4所示隶属度函数进行设定。
当q(k)∈(0.5,2)时,认为残差实测方差与理论方差比值在1附近,可信度为1;当q(k)∈(0,0.1)∪(10,∞)时,残差实测方差是理论方差的不到1/10或10倍以上,此时已远偏离1,所以认为可信度为0;当q(k)∈(0.1,0.5)∪(2,10)时,可信度随q(k)在[0,1]区间线性变化。
假设联邦滤波算法有两个子系统,通过模糊逻辑观测器对两个子系统进行可信度加权融合。模式一滤波器可信记为S1,残差比值为q1(k);模式二滤波器可信记为S2,残差比值为q2(k);模式一与模式二组成的联邦滤波器可信记为S3(S3=S1∩S2);模式一与模式二均不可信记为S0。
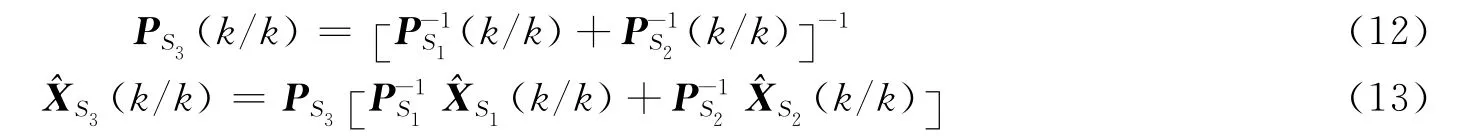
k时刻的最终融合结果为

k时刻的预测值同经典的卡尔曼滤波,其中β为各个滤波器的加权系数。
4 仿真分析
算法有两个子系统:子系统一为星光陀螺,子系统二为红外地平仪加太阳敏感器。系统状态方程采用文献[7]所建状态方程,主要仿真参数选取为:陀螺测量噪声均方差为0.1(°)/h,驱动白噪声标准差为0.06(°)/h,红外地平仪常值测量偏差为0.2°,测量噪声均方差为0.1°,太阳敏感器的测量噪声均方差为0.01°,星敏感器的测量噪声均方差为20″,轨道角速度为-0.0573(°)/s[8-9]。采用基于可信度加权自适应联邦滤波算法进行仿真,结果如图5、图6所示。从图5、图6可以看出,在初始时刻设定的误差角度较大的情况下,基于可信度加权自适应联邦滤波算法收敛速度很快,姿态估计误差在500s内收敛到0.01°,基于可信度加权模糊自适应卡尔曼滤波的联邦滤波算法可以及时根据各子系统传感器性能的变化调整子系统滤波器权值,有效地抑制故障子系统输出对全局估计的影响。

图5 姿态估计误差Fig.5 Estimation error of attitude
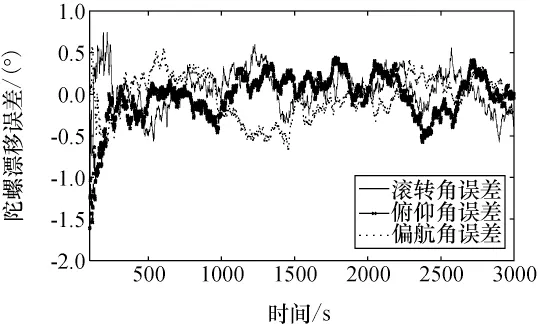
图6 陀螺漂移估计误差Fig.6 Estimation error of gyro-drift
5 结束语
卡尔曼滤波采用常值噪声矩阵,无法反映各子系统量测噪声统计特性的变化,使得子系统估计误差变大,最终导致联邦卡尔曼滤波器出现估计误差变大,甚至滤波发散。本文在联邦卡尔曼滤波子系统中采用自适应卡尔曼滤波,形成自适应联邦卡尔曼滤波算法,并采用模糊推理机制,判断子滤波器的加权系数,使模型量测噪声逐渐逼近真实噪声水平。将该算法应用于多传感器卫星姿态确定系统,仿真结果验证了算法的有效性。
[1]顾启泰,尚捷,毛刚.MIMS/GPS 组合导航系统设计与实验 [J].航空学报,2003,24(3):269-272.GU QITAI,SHANG JIE,MAO GANG.Design and experiment of MIMS/GPS integrated navigation system [J].Acta Aeronauticaet Astronautica Sinica,2003,24(3):269-272.
[2]BAR SHALOM Y,KIRUBARAJAN T.Estimation with applications to tracking and navigation:theory,algorithms,and software[M].New York:John Wiley & Sons.2001:373-400.
[3]CARLSON N A.Federated square filter for decentrealized parallel processes [J].IEEE Transactions on Aerospace and Electric.1999,26(3):517-524.
[4]ESCAMILLA AMHROSIO P J,MO N.A development of fuzzy logic[C]∥Proceedings of the Fifth International Conference on Information Fusion USA:Annapolis,2002:1542-1549.
[5]FRANCOIS C,EMMANUEL D,DENIS P,et al.GPS/INS data fusion using multisensor Kalman filtering introduction of contextual aspects[J].Information Fusion,2006,7(2):221-230.
[6]SASIAKEK J Z,WANG Q,ZEREMBA M B.Fuzzy adaptive Kalman filtering for INSPGPS data fusion [J].AIAA,1999,4307:1912-1917.
[7]潘旺华.基于多传感器信息融合的卫星姿态确定技术研究 [D].长沙:国防科技大学,2004.PAN WANGHUA.Research on the attitude determination of satellites based on the multi-sensor information fusion [C].Changsha:National University of Defense Technology,2004.
[8]GROCHOLSKY B.Information-theoretic control of multiple sensor platforms[C].Sydney:The University of Sydney,2002:57-84.
[9]BARSHALOM Y,RONG LI X,KIRUBAJAN T.Estimation with applications to tracking and navigation theory algorithms and software[M].New York:John Wiley & Sons,2001:1768-1773.
