“嫦娥二号”卫星L2点角动量管理

戴居峰 徐红兵 崔雁 薛锐

（1北京控制工程研究所，北京100190）（2北京航天飞行控制中心，北京 100094）

1 引言

对卫星的角动量进行管理，从而减少角动量饱和导致的喷气卸载，可以有效保持卫星在日地拉格朗日L2点绕飞的轨道，达到长期驻留的目的。国内外已经开始研究对在轨航天器的角动量进行管理的方法，以达到减少喷气卸载的目的，这对工作轨道要求较高、寿命要求较长的航天器是十分有意义的。目前对航天器角动量的管理尚未形成比较完备的方法，多数的方法是基于姿态控制和角动量控制联合考虑，取得了一定的效果。但同时也存在影响姿态控制性能、或者不能完全对角动量进行管理的不足之处。

“嫦娥二号”（CE－2）卫星于2011年9月1日进入日地拉格朗日L2点环绕轨道运行。L2点环绕轨道为不稳定轨道，由于角动量喷气卸载导致的速度误差会以每个月5倍的速度迅速放大，最终造成脱离目标轨道，甚至飞离L2点。因此，对CE－2卫星的角动量进行控制的意义较大。L2点卫星的干扰力矩很单纯，太阳光压力矩占绝对优势，而利用对卫星太阳翼的主动控制，能够实现利用光压管理角动量的目的。

本文在对太阳光压力矩进行分析的基础上，将光压干扰力矩分解为投影形状不对称引起的干扰力矩和涡轮力矩，并提出了基于太阳光压的角动量管理的方法。分别利用对日慢旋和太阳翼主动控制实现了对两种干扰力矩引起的角动量变化的全面管理，CE－2卫星的在轨飞行结果表明，该方法有效抑制了星体角动量累计，大幅度延长了卫星喷气卸载间隔。

2 太阳光压力矩分析

2.1 太阳光压力

在地球附近，太阳光功率密度约为I＝1 300W／m2（L2点位置），光冲量H＝E／c＝IAt／c。其中，E为光通量，A为受晒面积，c为光速。

由于太阳光压力矩F＝d H／dt，不难得到，F＝IAdt／cdt＝IA／c＝PA 。其中，P＝I／c，为太阳光压强。根据光速和地球太阳光功率，得到P＝4.3×10－6Pa。该压强为太阳光压的基础压强，是对应于全吸收表面的压强。对于带有反射情况的表面，需要利用基础压强进行分解计算［1－3］。

太阳光压力包括3个部分：吸收部分、全反射部分、漫反射部分。

为方便研究，将太阳光压分解为入射光方向（X 向）和垂直入射光方向（Z 向）。太阳光压全反射部分产生的光压力如图1所示，不难得到：

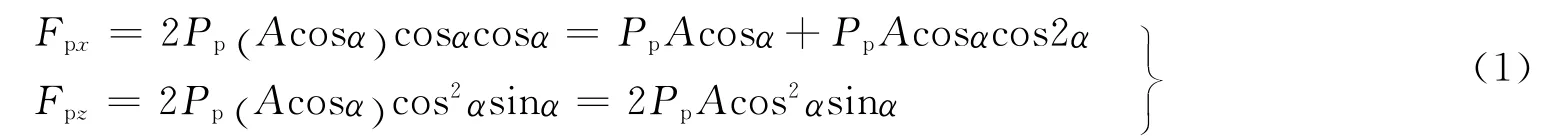
式中 Pp为太阳光的全反射部分的基础压强；Fpx、Fpz分别为全反射太阳光压力在X 向和Z 向的投影。

太阳光压漫反射部分产生的光压力如图2所示。按照理想的兰伯特漫反射理论，设正对法线的反射光强度密度为h，则与法线夹角为θ的反射线强度密度为hcosθ。将光强沿漫反射球积分即为漫反射总强度，该强度与入射光相等，即：其中Ab为球表面，Pd为太阳光的漫反射部分的基础压强。利用球坐标积分不难得到：

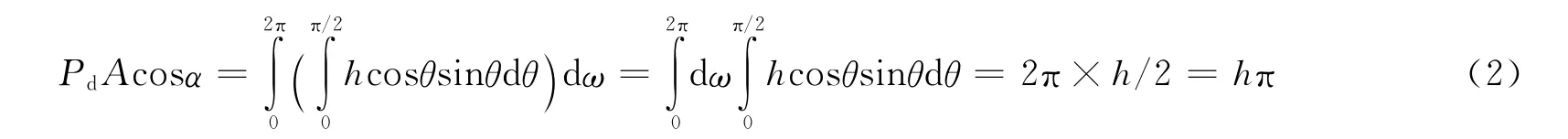
式中 ω为太阳翼相对卫星本体的角速度。由于反射光在空间上相对反射面法线对称，因此反射线的光压在反射面上的分量相互抵消，只在法线方向产生光压。根据兰伯特的强度理论，可以得到：

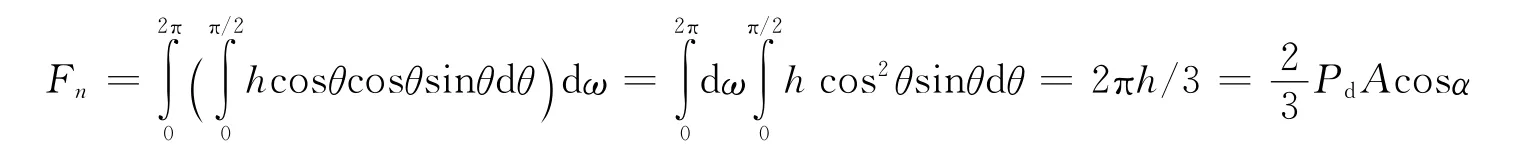
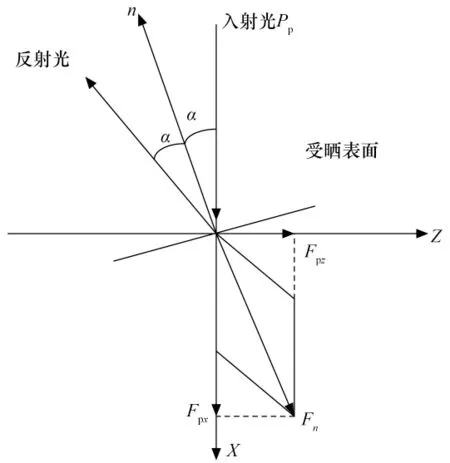
图1 全反射情况下的光压力Fig.1 Light pressure in the case of total reflection

图2 漫反射情况下的光压力Fig.2 Light pressure in the case of diffuse reflection

漫反射情况下，考虑到反射面对入射光的阻碍作用，光压在X、Z 方向的分量为

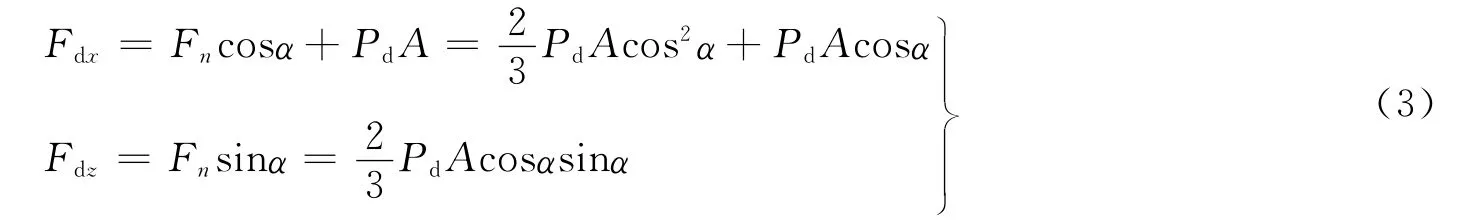
综合式（1）～（3），得到太阳光压力：

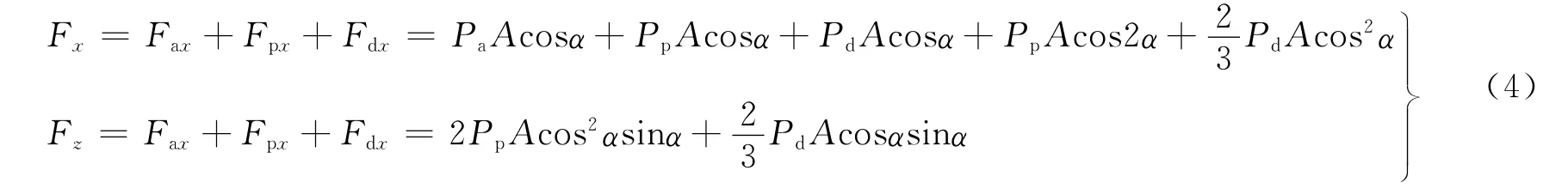
前文提到，太阳光压包括吸收、全反射、漫反射3个部分，即P＝Pa＋Pp＋Pd，令Pp＝ρP，Pd＝δP，其中，ρ、δ分别为全反射系数和漫反射系数，Pa为吸收部分的压强。式（4）可以整理为

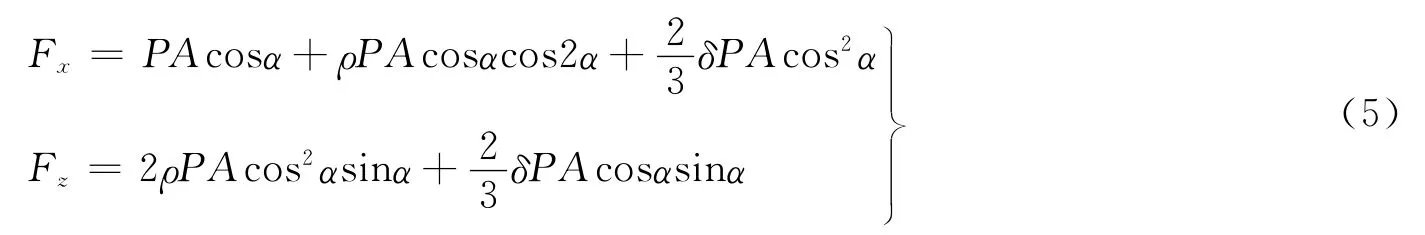
式（5）说明在X 向，光压包括两个部分，即对入射光阻碍导致的压力和对入射光反射导致的压力；在Z 向，只包含对入射光反射的光压［4－5］。

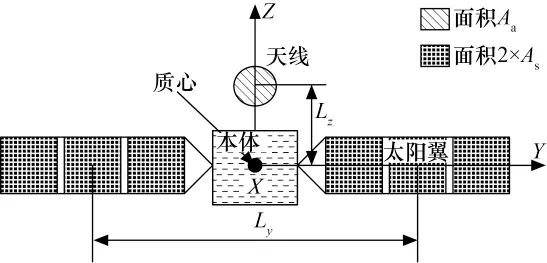
图3 非几何对称卫星示意Fig.3 Schematic diagram of geometrically asymmetric satellite

2.2 太阳光压力矩

（1）几何不对称导致的光压力矩

卫星受晒表面会产生太阳光压力，而几何不对称的卫星由于太阳光压力的压心与质心不重合，会由于光压导致干扰力矩［2，5］。假设卫星受晒表面投影如图3所示。

当＋X 指向太阳方向时，显然天线是星体上最大的几何不对称因素。作用在天线上的太阳光压力会产生－Y 方向的力矩。该干扰力矩定义为Tn，始终位于星体－Y 方向，力矩向量模为

式中 Fay为作用在天线上的太阳光压。几何不对称卫星的干扰力矩具有如下特点：1）对于任意不对称受晒表面，其干扰力矩均位于与太阳矢量垂直的平面内；2）干扰力矩在卫星本体系中各轴的投影不变。

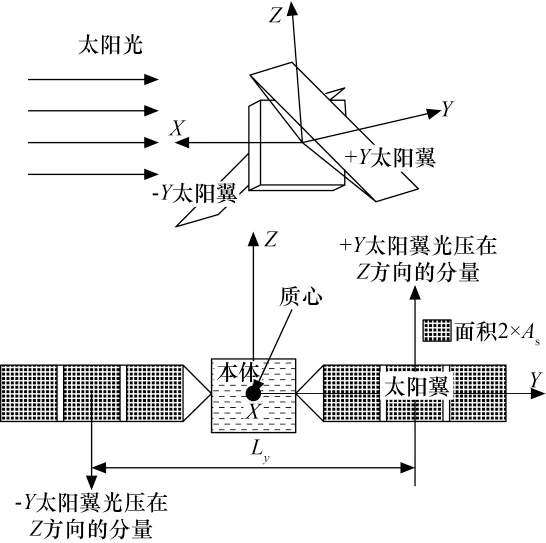
图4 绕太阳矢量方向的光压力矩产生原理Fig.4 Principle for generation of light pressure moment around sunlight vector direction

（2）沿太阳矢量方向的干扰力矩

卫星受晒面积几何不对称不会产生绕太阳矢量方向的干扰力矩，但当太阳翼转角不同时，由于太阳翼对阳光的反射作用将导致绕太阳矢量方向的干扰力矩。如图4所示，＋Y 太阳翼绕Y 轴转动了α，－Y 太阳翼绕Y 轴转动了－α，导致光压因反射作用产生了Z 方向光压力，且两侧太阳翼的光压力方向相反。

如图4所示，两侧太阳翼的Z 方向分量极性相反，因此形成力偶，产生＋X 方向（太阳矢量方向）力矩。令太阳矢量方向力矩为Tw，则有：Tw＝FzLy，将式（5）代入其中，并令A＝AS，得到：

这种因太阳翼转角不同造成的绕太阳方向的光压力矩类似于涡轮在绕气流方向的转动，本文后面称其为“涡轮”力矩Tw。涡轮力矩具有特点：1）涡轮力矩与受晒面投影几何对称性无关；2）涡轮力矩方向平行于太阳矢量方向。

3 利用太阳光压的角动量管理

3.1 利用对日自旋进行角动量管理

在允许的情况下对日稳定自旋可有效降低角动量累积。如图4所示，设星体＋X 轴指向太阳，且绕＋X 轴以角速度ω 匀速转动。星体上的太阳光压力矩可表述为T＝Tw＋Tn，其中Tw、T 均与本体坐标系固连，该力矩在匀速转动一周后的角动量累积为

式中 H为绕X 轴转动一周的累积角动量。考虑到光压力矩与本体固连，因此光压力矩在本体系下可表示为T＝Tw＋Tn＝（xbybzb）（TwTnyTnz）T，其中（xbybzb）为本体系基向量。考虑到星体绕X 轴转动，光压力矩在惯性系下可表示为

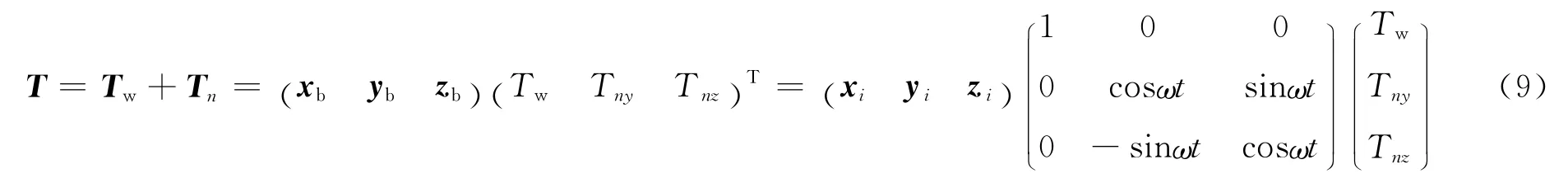
将式（9）代入式（8）可以得到：

从式（10）中不难看出，在星体匀速自旋情况下，因受晒面几何不对称，导致的干扰力矩经过一圈积分，产生的角动量为0；涡轮力矩会导致星体X 方向的角动量累积。

3.2 利用涡轮力矩的角动量管理

如3.1节所述，通过绕太阳矢量自旋，只要角速度稳定，可以有效抑制卫星在垂直太阳矢量方向的角动量累积，但对太阳矢量方向的累积没有作用。在光压作用下，只有涡轮力矩能够产生太阳矢量方向的力矩，涡轮力矩多数情况下是干扰力矩，但通过对太阳翼的交叉控制，如图4所示，可以实现对涡轮力矩的主动控制，将其用于角动量卸载。

将式（7）整理如下：

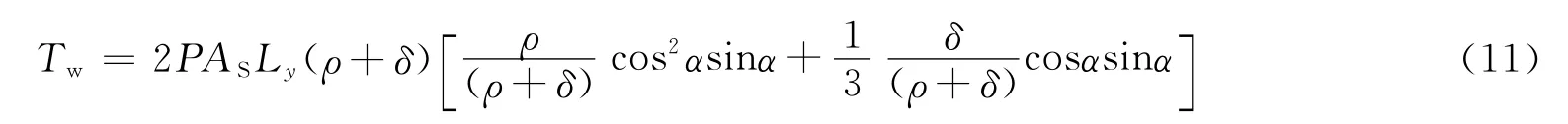
式（11）显然是一个转角α的周期函数，且与全反射系数、漫反射系数在总反射系数中所占比例有关。α＝35°、α＝45°分别对应着式（8）全反射部分（δ＝0）和漫反射部分（ρ＝0）的最大值。因此在轨使用主动涡轮力矩控制时，太阳翼的控制角不应超过45°。

4 针对CE－2的光压卸载

CE－2卫星在进入L2点环绕轨道后就开始了对日稳定慢旋，飞行结果表明，经过60天的飞行，卫星在垂直太阳矢量方向上角动量累计小于0.5kg.m2／s，成功抑制了由于投影几何不对称导致的角动量累计。但是在太阳矢量方向上，卫星以每天0.1kg.m2／s的速度累计了约6kg.m2／s的角动量，根据前文分析不难看出，该角动量的累计与两侧太阳翼存在微量差动有关。

2011年12月20日，地面主动控制卫星进行了涡轮力矩主动控制，先控制太阳翼转角使星体绕太阳矢量的角动量由5kg.m2／s增加到8kg.m2／s，然后反向控制太阳翼转角将该角动量又降低到－1.7kg.m2／s。试验结果表明，涡轮力矩真实存在，且能够通过太阳翼主动控制加以利用，效果明显。

2011年12月～2012年1月在轨进行试验的角动量数据曲线如图5、6所示，并对角动量数据进行了拟合处理，以获得角动量变化的规律。其中图5为太阳翼差动偏置5.6°时星体角动量变化情况，经过对角动量数据进行拟合分析，此时涡轮力矩达到每天2.59kg.m2／s；图6为当太阳翼差动－20.1°时星体角动量变化情况，经过对角动量数据进行拟合分析得出涡轮力矩为每天累计－7.86kg.m2／s。将上述两次偏置的角度和力矩结果带入式（11），经过方程求解，不难得到太阳翼全反射系数ρ＝0.22，δ＝0.07，即入射太阳光有22%发生全反射，7%发生漫反射，该结果在合理范围内，这就证实本文的光压力矩分析是正确的。

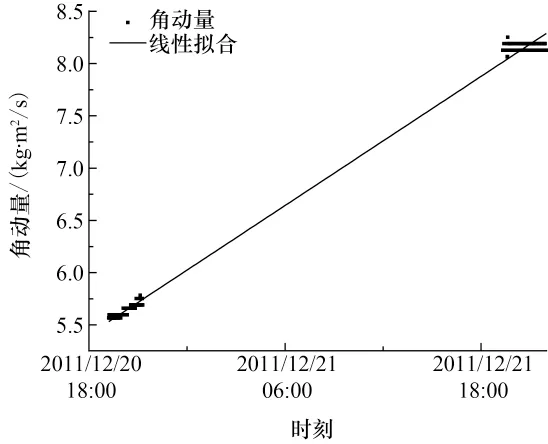
图5 太阳翼偏置5.6°涡轮力矩在轨数据Fig.5 Orbital data on the turbine torque of solar wing biased 5.6°

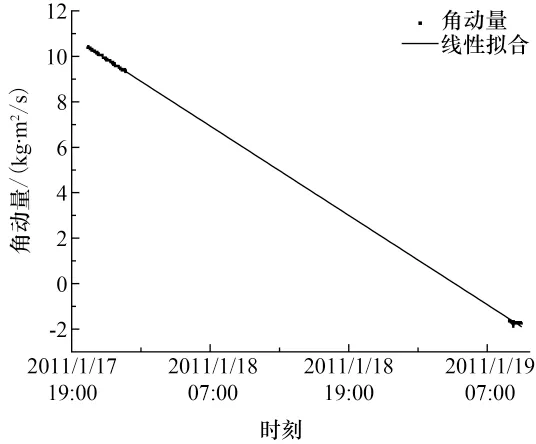
图6 太阳翼偏置20.1°涡轮力矩在轨数据Fig.6 Orbital data on the turbine torque of solar wing biased 20.1°

5 结束语

在日地拉格朗日L2点，太阳光压力矩是占绝对优势的环境力矩。通过星体对日自旋，可以消除环境力矩在对日面内的影响。通过对太阳翼的控制能够产生涡轮力矩，对星体沿太阳矢量方向的角动量实现主动管理。该方法与常规的角动量管理的思路不同，通过太阳翼主动控制，能够利用阳光反射产生涡轮力矩，成功抑制角动量的累计。在轨实际力矩大小与计算结果基本吻合，并能够通过卸载量的大小间接计算出太阳翼的全反射系数和漫反射系数。该方法对航天器在轨的角动量管理进行了有益的尝试并取得了较好的效果，可以进一步应用此方法开展对于近地航天器的在轨角动量管理的尝试。

［1］刘墩，赵志萍.卫星太阳光压力矩计算中有效作用面积的计算 ［J］.南京理工大学学报，2007，31（6）：685－688.LIU DUN，ZHAO ZHIPING.Method to calculate effective area used in computation of solar radiation torque of satellite［J］.Journal of Nanjing University of Science and Technology，2007，31（6）：685－688.

［2］崔文，王家松，宝音贺西.光压摄动对卫星姿态轨道耦合的影响分析 ［J］.空间科学学报，2012，32（3）：424－429.CUI WEN，WANG JIASONG，BAOYIN HEXI.Analysis of solar pressure perturbation impacting on satellite attitude－orbit coupling ［J］.Chinese Journal Space Science，2012，32（3）：424－429.

［3］王春成，张旭东，黄文浩，等.探月飞行中太阳帆航天器帆面光学性能演化 ［J］.中国科学技术大学学报，2007，31（1）：82－86.WANG CHUNCHENG，ZHANG XUDONG，HUANG WENHAO，et al.Optical performance evolution of solar sail－driven lunar probe［J］.Journal of University of Science and Technology of China，2007，31（1）：82－86.

［4］石顺详.物理光学与应用光学 ［M］.西安：西安电子科技大学出版社，2001.

［5］李连军，戴金海.双翼箱式航天器太阳光压干扰力矩模型 ［J］.航天控制，2005，23（4）：13－17.LI LIANJUN，DAI JINHAI.Model of sunlight pressure disturbance torque on cubical spacecraft with a pair of solar sails［J］.Aerospace Control，2005，23（4）：13－17.