基于间接法的最优小推力逃逸轨道设计

黄镐 韩潮

（北京航空航天大学宇航学院，北京 100191）

1 引言

在小推力星际探测任务中，逃逸捕获阶段因其多圈螺旋轨道的特性而在整个任务过程中最为复杂。目前，基于小推力的轨道优化设计方法可归结为直接法和间接法。直接法采用离散配点法将最优控制问题转化成高维非线性参数规划问题，鲁棒性较好，对于单圈或圈数较少的轨道转移问题比较适用；但对于多圈（大于50圈）螺旋逃逸轨道设计，采用直接法将形成庞大的非线性参数规划问题，导致求解难度非常大［1］。间接法利用庞特里亚金极值原理将最优控制问题转化成两点边值问题，未知协状态量维数较少，而且求解的精度高，但两点边值问题对协状态量初值非常敏感，对于多圈长时间逃逸问题，该问题尤甚，要得到收敛解需要提供非常好的初值猜测，然而协状态变量没有实际物理意义，初值很难猜测，甚至其量级都无法界定，由此给间接法的应用带来了不小困难。目前，国内外已有一些利用间接法进行逃逸螺旋轨迹优化的研究［2－5］，也有一些研究在求解整个星际探测任务中考虑了逃逸阶段［5－6］。这些研究中，普遍采用了一种协状态控制转换技术（ACT）［3］来降低两点边值问题初值的敏感性，且大部分都只研究了控制无约束的平面内逃逸问题，或者采用逃逸时间［2］或逃逸能量［5］作为优化性能指标。

本文采用间接法［7］求解小推力燃料最优逃逸问题，通过引入一个待定参数，求解了复杂的长时间控制有约束的三维燃料最优逃逸问题。

2 地心球惯性坐标系下轨道动力学方程

在地心惯性系中的位置、速度矢量用r和v表示；ex、ey、ez分别表示地心直角惯性系中x，y，z方向上的单位矢量；er、eθ、eφ分别为地心球惯坐标系各正交轴单位矢量，如图1所示。

地心球惯性坐标系下航天器轨道动力学系统状态量为x＝ ［r，θ，φ，vr，vθ，vφ］T，动力学方程为

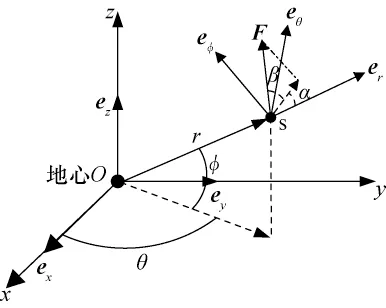
图1 直角坐标系与球坐标系之间关系Fig.1 Relation between cartesian and spherical system

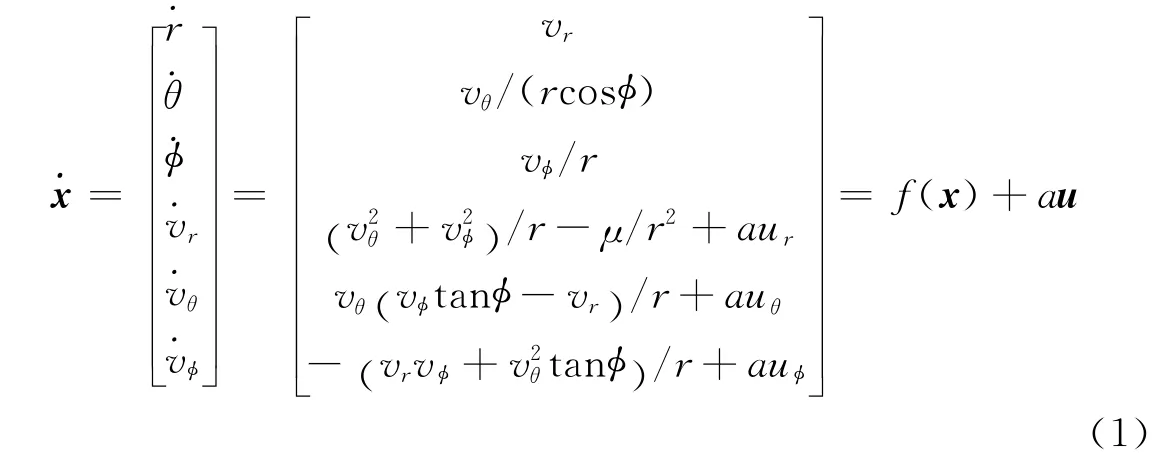
式中 r和a 分别为位置和推力加速度幅值；μ为地球引力常数；u为推力方向矢量，可由角α和角β 来描述。

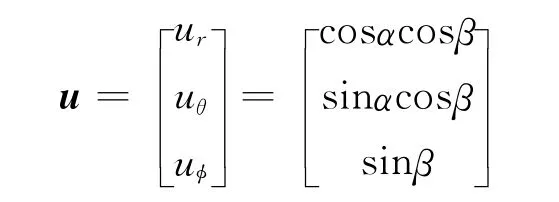
对于变比冲小推力发动机模型，航天器加速度模型可表示为

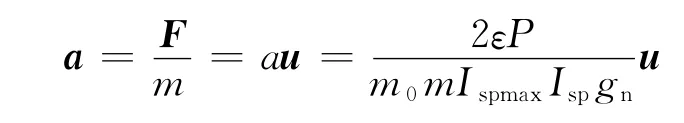
式中 F和a分别表示航天器推力和推力加速度矢量；ε为发动机效率；P为固定的发动机功率；gn为标称重力加速度；m0和Ispmax分别表示航天器初始质量和发动机最大比冲；m 和Isp则为对应的归一化处理后的系数，m ∈［（m0－mfuel）／m0，1］，Isp∈［Ispmin／Ispmax，1］；mfuel为航天器燃料总质量；Ispmin为变比冲发动机能提供的最小比冲。质量导数方程为

3 燃料最优控制问题

对于变比冲发动机燃料最优逃逸问题，可描述为在初始轨道给定的情况下，在固定时间通过控制发动机比冲Isp的大小以及推力矢量方向，使得航天器轨道能量在达到逃逸能量的同时，所消耗的燃料最少。对应的性能指标和初始条件的数学描述为

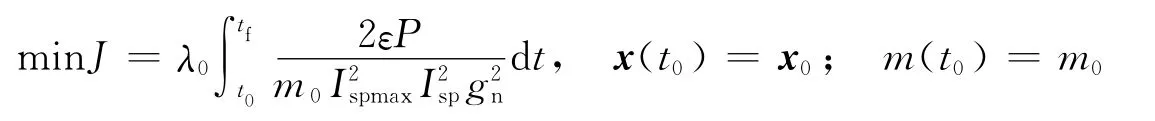
式中 t0和tf分别为逃逸始末时刻；λ0为引入性能指标函数中大于零的待定参数，若λ0＝1即为原问题；若λ0≠1，只要λ0＞0，就不会改变系统燃料最优的本质。下标0、f分别表示初始时刻和终点时刻对应的参量。

由庞特里亚金极小值原理［8］，推导系统Hamilton函数及最优控制为

式中 λ＝［λr，λθ，λφ，λvr，λvθ，λvφ］T为与状态量x相对应的协状态量向量；λv＝［λvr，λvθ，λvφ］T为与速度v对应的协状态量向量；λm为与m 对应的协状态量。

由∂H／∂u＝0，推导系统最优控制方向矢量为

将公式（3）带入Hamilton函数得：

进一步推导最优Isp控制为

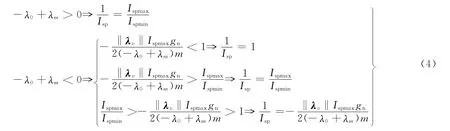
系统协状态方程为

燃料最优逃逸问题的终端约束为终点时刻tf时的轨道能量εf达到抛物线逃逸轨道能量值εtar。

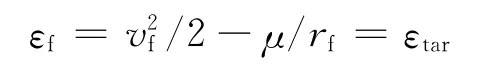
抛物线逃逸轨道的能量εtar≡0。由文献 ［8］得到系统增广约束为

式中 υ为引入的增广系数。对应的系统横截条件为

对于燃料最优逃逸问题，由公式（5）、（7）可知˙λθ＝0，且λθf＝0，所以λθ≡0。公式（1）、（2）、（5）、（6）、（7）、（8）共同构成两点边值问题。若λ0＝1，即为原问题，则由系统Hamilton函数推导出的两点边值问题待定参数向量为［λr0，λφ0，λvr0，λvθ0，λvφ0，λm0，υ］，由于这些变量的取值范围没有任何先验的初始判断，所以对于其初值的猜测难度非常大；若在性能指标函数中引入的正数λ0为待定参量，则系统待定参数向量为［λ0，λr0，λφ0，λvr0，λvθ0，λvφ0，λm0，υ］，虽然比原问题维数增加了一维，但却在不改变原优化问题的前提下使得系统Hamilton函数中各加减项同质［7］，若将系统Hamilton函数除以大于零的比例系数K，将在不改变Hamilton函数的极值属性前提下得到新系统Hamilton函数，定义K为待确定参数向量的模值，即

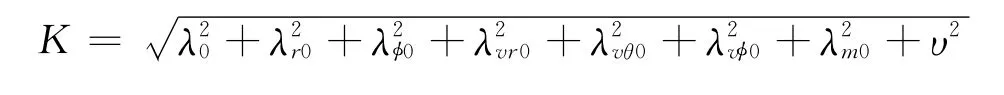
则由新系统Hamilton函数推导的两点边值问题的解向量便为原系统待确定参数向量除以比例系数K，即为原系统待确定参数向量的单位化：

由此可知新系统Hamilton函数推导的两点边值问题的待定参数向量将被约束在一个多维的单位球里。相对于原系统Hamilton函数推导的两点边值问题，待定参数向量取值范围无任何先验判断，而由引入未知变量λ0和比例系数K 构成的新系统Hamilton函数推导的两点边值问题，每个待确定参数的初值猜测范围将被约束在区间 ［－1，1］中，由此将大大提高两点边值问题的初值猜测效率，进而提高问题的收敛性。在求解出由新系统Hamilton函数推导的两点边值问题待定参数向量之后，通过除以λ＊0，即，将得到原问题系统Hamilton推导的两点边值问题的解向量。

对于由新系统Hamilton函数推导的两点边值问题共有8个待确定变量，对应的约束条件也为8个：

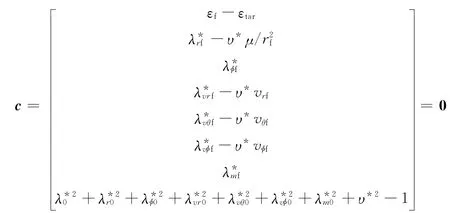
在通过打靶法求解上述待定参数后，对公式（1）、（2）、（5）、（6）积分可求得各时刻轨道状态量和协状态，由公式（3）和公式（4）可求得发动机推力矢量和最优Isp控制。

4 仿真算例

设地球逃逸的初始停泊轨道为半径为7 500km 的赤道平面内圆轨道，由于设计参数与θ无关，可以假设初始轨道的真近点角为0°，航天器总质量为100 000kg，发动机固定功率为5MW，效率为1。

4.1 平面内控制有约束长时间燃料最优地球逃逸

直接采用间接法求解平面内控制有约束长时间燃料最优地球逃逸非常困难，为此，将问题分解为两步：首先由短时间控制无约束最优逃逸逐步求解长时间控制无约束最优逃逸；其次由长时间控制无约束最优逃逸逐步求解长时间控制有约束最优逃逸。

以30天Isp∈［3 600m／s，6 600m／s］区间的燃料最优逃逸问题为例，先以0.05天为间隔，分别求解出0.1～5天的燃料最优逃逸的收敛解；采用数值曲线拟合技术对0.1～5天的收敛解进行拟合，用于外推猜测5～10 天的未知参量初值，进而求解5～10 天燃料最优逃逸的收敛解；有了10天的收敛解，拟合形成10～30天的初值猜测；当采用该拟合曲线给出的初值不能收敛的时候，则利用该发散时刻以前的所有已收敛结果，重新拟合出新的曲线，重新计算该点初值，然后重新打靶计算。在仿真试验过程中，通过求解最初1～5天燃料最优逃逸问题发现，协状态量λvr0变化较大，规律不明显，曲线拟合难度较大。为此，借鉴文献［3］的方法，令在协状态量λvr0随逃逸时间tf变化规律性出现之前，采用拟合b0和λvθ0，然后计算λvr0的初值猜测。

根据0.1～30天的仿真试验数据，结合曲线拟合技术，得出在采用如下曲线拟合公式时，能最好地拟合出各待定参数随逃逸时间tf的变化关系

式中 p1，p2，q1，q2为相应的拟合系数。各待定参数的拟合系数如表1所示，各待定参数对应的拟合曲线与其收敛解之间的关系如图2、图3所示。图2、3中“◇”为各待定参数的收敛解，实线为各待定参数的拟合曲线。可以看出，采用曲线拟合公式（9）和表1中的参数，对各待定参数拟合效果非常好。

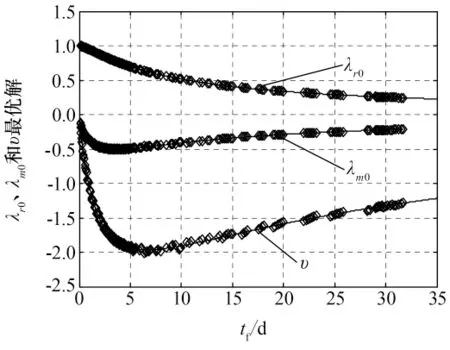
图2 λr0、λm0和v最优解与逃逸时间关系Fig.2 Optimal solution and escape time of λr0，λm0and v

图3 b0、λvr0和λvθ0最优解与逃逸时间关系Fig.3 Optimal solution and escape time of b0，λvr0andλvθ0

表1 平面内Isp无约束地球逃逸初值猜测拟合曲线系数（a＝7 500km，e＝0）Tab.1 Estimation coefficients for earth escape without Ispconstraints（a＝7 500km，e＝0）

采用拟合公式（9）和表1中的系数，拟合得到tf为30天燃料最优逃逸问题各待定参数的初值猜测，迭代打靶求解平面内30天Isp无约束燃料最优逃逸问题。在得到平面内30天Isp无约束燃料最优逃逸问题收敛解的基础上，以此为初值，利用同伦思想逐步将Isp控制约束从［3 000m／s，10 000 m／s］区间调整为实际的［3 600m／s，5 400m／s］区间，最终求得Isp属于［3 600m／s，5 400m／s］区间的有约束平面内逃逸问题的收敛解。结果表面，航天器在30天中绕地球飞行118圈后达到地球逃逸速度，整个过程共消耗燃料13 634kg，占总质量的13.6%。Isp无约束、Isp∈［3 600m／s，6 600 m／s］和Isp∈［3 600m／s，5 400m／s］的30天燃料最优平面内逃逸轨道如图4所示，相应的Isp随转移时间变化的曲线如图5所示。由图4可以看出，Isp控制从无约束到最终约束在［3 600m／s，5 400 m／s］区间的过程中，逃逸圈数没有变，依然为118圈，只是逃逸轨迹上有些微小的变化；图5则清晰地反映了Isp控制由无约束到约束逐步变严，到最终约束在［3 600m／s，5 400m／s］区间的过程。

图4 平面内30天燃料最优地球逃逸轨迹Fig.4 Fuel optimal earth escape trajectory for 30days in planar

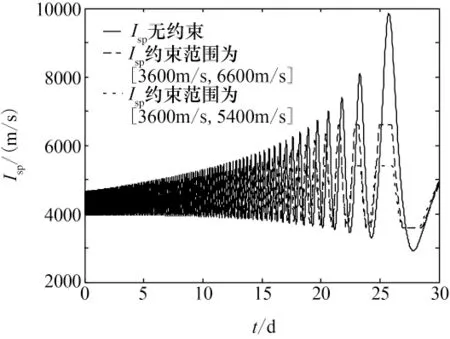
图5 Isp随时间变化曲线Fig.5 Relations between Ispand transfer time

4.2 三维控制有约束长时间燃料最优地球逃逸

对于三维逃逸问题，在逃逸点加上轨道倾角约束，假定航天器相对于地球以特定的轨道倾角逃逸。

轨道倾角在球坐标系中可表示为

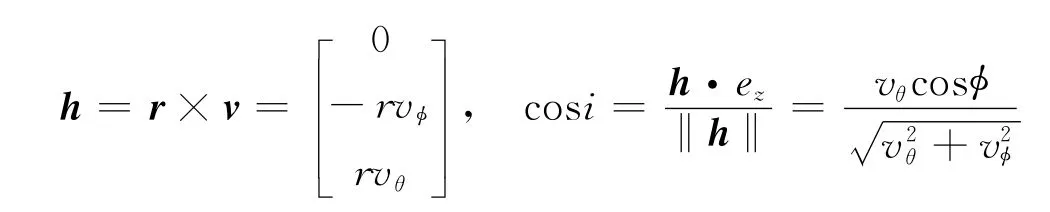
式中 h为航天器的角动量；i为轨道倾角。在逃逸点加上倾角约束之后，燃料最优逃逸问题的增广约束方程为

式中 γ为由加入倾角约束而引入的待确定增广系数；itar为三维逃逸问题的目标倾角要求。

利用Isp无约束平面内燃料最优逃逸问题的解作为初值猜测，可逐步求得Isp无约束三维燃料最优逃逸问题的解；有了Isp无约束三维燃料最优逃逸问题的解，逐步加入Isp控制约束，进而最终求解Isp有约束三维燃料最优逃逸问题。仿真同样以半长轴为7 500km 的地球赤道圆轨道为初始停泊轨道，假定要求30天后达到逃逸能量，Isp约束范围为 ［2 700m／s，6 500m／s］，且逃逸点轨道倾角为30°。以Isp无约束平面内30天燃料最优逃逸的最优解为初值，将终端轨道倾角约束由3°开始，逐步加大到最终设计的逃逸倾角，即30°，上一步得到的最优解作为下一步计算的初值猜测，最终求解Isp无约束、末端30°倾角的燃料最优逃逸问题。在得到Isp无约束30°燃料最优逃逸收敛解之后，以此为初值，逐步加严Isp控制约束，同样利用上一步得到的最优解作为下一步计算的初值猜测，最终求得Isp∈［2 700m／s，6 500m／s］的30°燃料最优逃逸轨道。图6给出了逃逸倾角为30°、Isp约束范围为 ［2 700m／s，6 500m／s］的30天燃料最优逃逸轨迹，航天器逃逸过程共绕地球飞行118圈，消耗燃料14489.6kg，约占总质量的14.5%；图7给出了30°倾角逃逸，Isp无约束和有约束情况下Isp随转移时间变化的关系曲线，可以看出，Isp有约束和无约束随转移时间变化规律基本相同，从另一个侧面说明了以无约束问题的收敛解作为有约束问题的初值猜测的合理性。

6 30天Isp有约束地球30°逃逸燃料最优逃逸轨迹Fig.6 30days earth escape trajectory under 30°

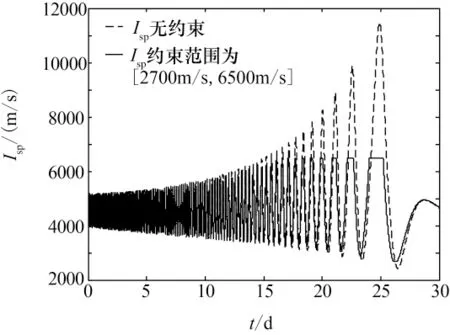
图7 地球30°燃料最优逃逸Isp随时间变化曲线Relations between Ispand transfer time under 30°

5 结束语

本文通过在燃料最优性能指标中引入待定参数，使由此推导的两点边值问题的各待定参数初值约束在 ［－1，1］区间内，初值猜测范围缩小，大大提高了间接法的收敛性。数值仿真结果表明，改进的间接法结合同伦思想和曲线拟合技术，能提供较好的初值猜测，从而减少迭代次数，提高收敛速度，能有效地求解复杂的长时间控制有约束三维逃逸问题，是一种高效的小推力逃逸轨道设计方法。此外，本文以小于0.5天的时间间隔，计算并绘制了逃逸时间从0.1～30天的控制无约束平面内燃料最优逃逸问题的最优解，其呈现出的规律趋势不仅可以用曲线拟合技术外推产生较好的长时间最优逃逸初值猜测，也将为进一步探索其中的规律提供一定的参考。

［1］BETTS J T.Very low－thrust trajectory optimization using a direct SQP method［J］.Journal of Computational and Applied Mathematics，2000，120：27－40.

［2］严辉，吴宏鑫，吴新珍.小推力轨道优化研究 ［J］.中国空间科学技术，1998，18（2）：8－13 YAN HUI，WU HONGXIN，WU XINZHEN.Study on optimization of low－thrust trajectories ［J］.Chinese Space Science and Technology，1998，18（2）：8－13.

［3］RANIERI C L，OCAMPO C A.Indirect optimization of spiral trajectories［J］.Journal of Guidance，Control，and Dynamics，2006，29（6）：1360－1366.

［4］LEE D H，BANG H.Efficient initial costates estimation for optimal spiral orbit transfer trajectories design［J］.Journal of Guidance，Control，and Dynamics，2009，32（6）：1943－1947.

［5］NAH R S，VADALI S R.Fuel－optimal，low－thrust，three－dimensional earth－mars trajectories［J］.Journal of Guidance，Control，and Dynamics，2001，24（6）：1100－1107.

［6］RANIERI C L，OCAMPO C A.Indirect optimization of three dimensional finite－burning interplanetary transfers including spiral dynamics［J］.Journal of Guidance，Control，and Dynamics，2009，32（2）：444－454.

［7］JIANG F H，BAOYIN H X，LI J F.Practical techniques for low－thrust trajectory optimization with homotopic approach ［J］.Journal of Guidance，Control，and Dynamics，2012，35（1）：245－258.

［8］HULL D G.Optimal control theory for applications［M］.New York：Springer，2003：199－247.