空间机械臂关节零部件对关节总刚度的影响分析
2013-11-26危清清王耀兵刘志全
危清清 王耀兵 刘志全
(中国空间技术研究院,北京100094)
1 引言
空间机械臂主要由臂杆和关节组成,臂杆材料一般采用低密度、高模量的碳纤维复合材料,自身质量不大,而关节一般由金属材料制成,是空间机械臂减小质量的重点对象。另一方面,空间机械臂关节是空间机械臂动力提供、位置感知和机械连接的核心部件,是保证机械臂运动能力、运动精度和运动平稳性的关键。关节刚度对整个机械臂刚度的影响很大[1],所以空间机械臂关节既是保证机械臂整体刚度的关键环节,又是有效减小质量的重点对象,而保持刚度与减小质量在一定程度上又相互矛盾。
空间机械臂关节电机仅能提供几牛顿米以内的输出力矩,若电机直接驱动,输出力矩无法满足机械臂辅助转位、对接等任务中所需几百到上千牛顿米的力矩需求,这使得空间机械臂关节传动系统必须具备较大的传动比来提高关节的输出力矩。然而,在空间机械臂中广泛应用的大传动比多级行星齿轮传动系统的结构复杂性[2]给刚度分析和减小质量都带来了困难。
加拿大机械臂关节[2]主要通过试验、参数辨识来实现刚度分析,此方法较为接近实际,但是无法反映关节各部件刚度对于关节总刚度的影响,对于关节减小质量及优化的指导作用不大。针对上述问题,本文采用集中参数法和刚度串联原理,建立复杂关节等效刚度模型,分析各级齿轮刚度对关节总刚度的影响,从而找出对总刚度影响不大的零部件,对其实施减小质量,为大传动比空间机械臂关节的小质量高刚度优化设计提供指导。
2 空间机械臂关节传动系统刚度模型建立
传动系统的刚度分析方法主要有有限元法与集中参数法。针对图1所示的大传动比齿轮传动系统,用有限元法建模,虽然求解精度高,适用于已定型传动系统的刚度校核,但建模较为复杂、计算量大、耗时多3,用于关节传动系统减小质量、优化设计的反复迭代分析不方便。集中参数法将传动系统构件简化为集中质量,将齿轮啮合力简化为集中力,构件之间的连接简化为弹簧。文献[3]证明了此方法的有效性。本文采用集中参数法来分析图1所示的多级行星齿轮传动系统各级齿轮对于传动系统总刚度的影响,探寻提高传动系统总刚度的方法,给关节减小质量及优化提供参考。
图1所示为一种典型的空间机械臂关节传动系统。根据每个齿轮及其所在的轴可以将其分为9组(见表1),对照图1和表1,这9组的转速随着序号的增加而依次降低,1、2、3组为高速级,4、5、6组为中速级,7、8、9组为低速级。电机提供的动力由输入轴l1经行星轮系A-B-C-h1,传递到定轴轮系H-I,然后通过定轴轮系J-K-L及差动轮系M-N(Ol,Or)-Q-h2,由齿轮Q带动输出轴输出。其中,L-M为含内齿圈L和外齿圈M的大齿轮。Ol与Or为齿数、模数均相同的两个同轴齿轮。下文分别对周转轮系与定轴轮系进行刚度建模与分析。
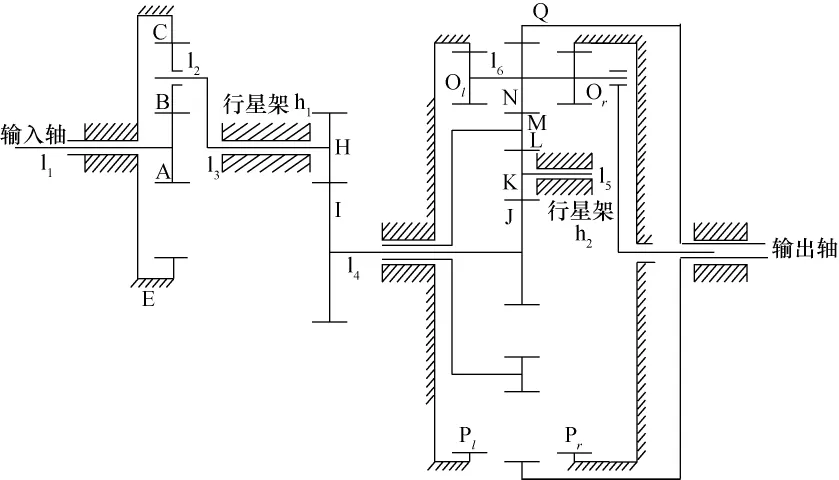
图1 关节齿轮传动系统Fig.1 Gear transmission system of the joint
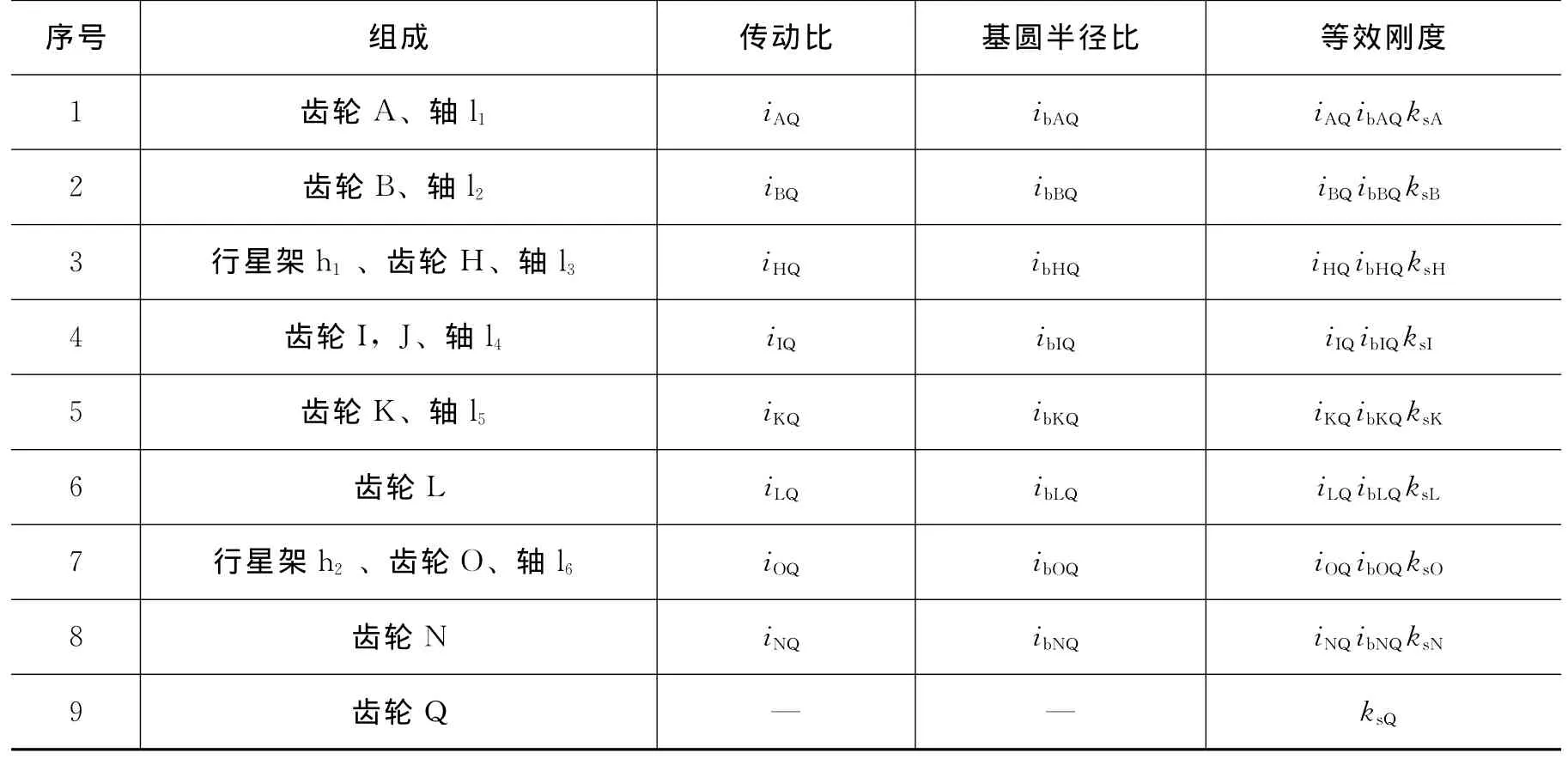
表1 传动系统各齿轮组相对于输出齿轮Q的传动比与等效刚度Tab.1 All the described gears′reduction rate and stiffness relative to gear Q
2.1 周转轮系的刚度模型
对于图1中 “A-B-C-h1”组成的行星轮系,将轮齿的啮合力简化为集中力,同时将轮齿啮合中产生的弹性变形转化为齿轮的角变形,齿轮的扭转刚度定义为:使齿轮沿啮合线上产生单位角变形所需的载荷[4-5]。
设kA是齿轮A的扭转刚度,kl1为轴l1的扭转刚度。则轴l1、齿轮A的总刚度ksA符合设kB是齿轮B的扭转刚度,kl2为轴l2的扭转刚度,则轴l2、齿轮B的总刚度ksB符合
同理可得,行星架h1、输出轴l3和齿轮H的总刚度ksH符合其中,N为行星轮的个数,kh1、kl3分别为行星架h1、轴l3的扭转刚度,kH为齿轮H的扭转刚度。
推导可得l1-A-B-C-h1-H的总刚度ksAH符合:
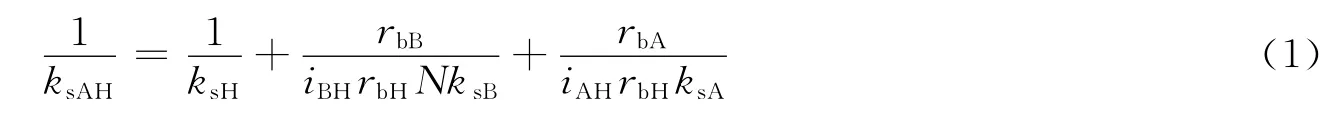
式中rbA、rbB和rbH分别为齿轮A、B和H的基圆半径;iAH和iBH分别为A→H与B→H的传动比。下文中传动比下标的含义均与此类似。
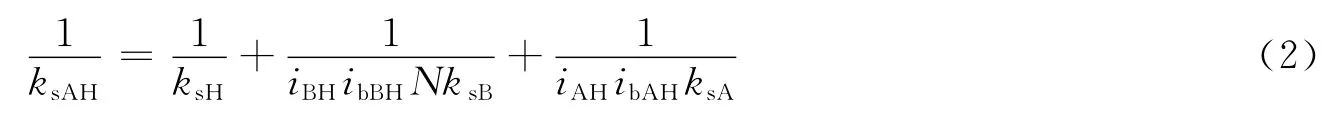
可见行星轮系总刚度与传动比和基圆半径比相关。设等效刚度keAH=iAHibAHksA,keBH=iBHibBHksB,则式(2)进一步简化为

因此,l1-A-B-C-h1-H的力学模型表示为图2,其中JA、JB和JH分别表示齿轮A、B和H的转动惯量。
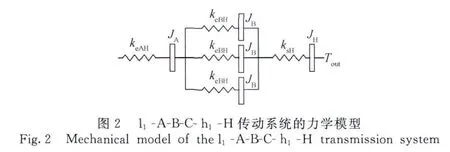
同理,将上述方法应用于差动轮系M-N(Ol,Or)-Q-h2可以建立其力学模型,其总刚度ksMQ符合:
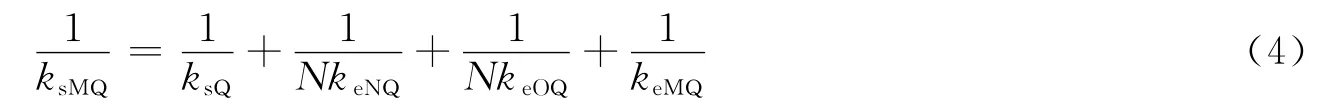
式中ksQ为齿轮Q的扭转刚度;keNQ和keMQ分别为齿轮N和M相对于齿轮Q的等效刚度;keOQ为齿轮Ol与Or的刚度和ksO相对于齿轮Q的等效刚度。等效刚度如表1所示。
2.2 定轴轮系的刚度模型
对于图1中的定轴轮系H-I-J,设kI为齿轮I的扭转刚度,kl4为轴l4的扭转刚度,kJ为齿轮J的扭转刚度。则轴l4与齿轮I,J的总刚度ksI符合
经推导,可得定轴轮系H-I-J的总刚度ksHI符合:

式中iHI为H→I的传动比。定义kesH=iHI2ksH为ksH相对于齿轮I的等效刚度,其中iHI2=iHI·ibHI,ibHI为齿轮H和I的基圆半径比,则式(5)可以写成[6]:

根据刚度串联原理,可将定轴轮系H-I-J的力学模型表示为图3形式,其中JI和JJ分别表示齿轮I和J的转动惯量。
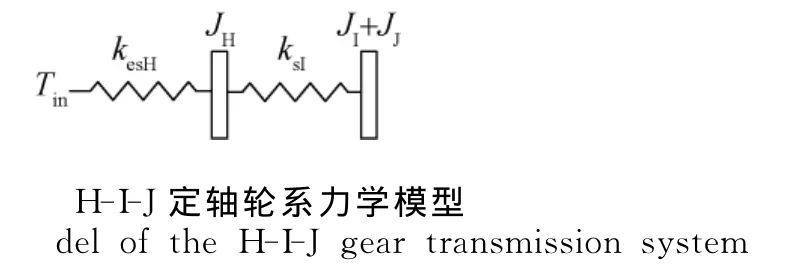
同理,可以建立定轴轮系J-K-L的力学模型,其总刚度ksJL符合:

式中ksL是齿轮L扭转刚度;keKL和keJL分别为齿轮K和J相对于齿轮L的等效刚度。
2.3 关节传动系统的刚度模型
基于上述周转轮系与定轴轮系刚度模型的建立,大型空间机械臂大传动比关节传动系统的力学模型可表示为图4,其中JO为齿轮Ol与Or的惯量和。各组齿轮相对于输出齿轮Q的等效刚度如表1所示。

图4 关节传动系统力学模型Fig.4 Mechanical model of the joint transmission system
表1中等效刚度的推导方法见本文第2.1~2.2节及文献[5-6]。则关节传动系统总刚度kesQ为
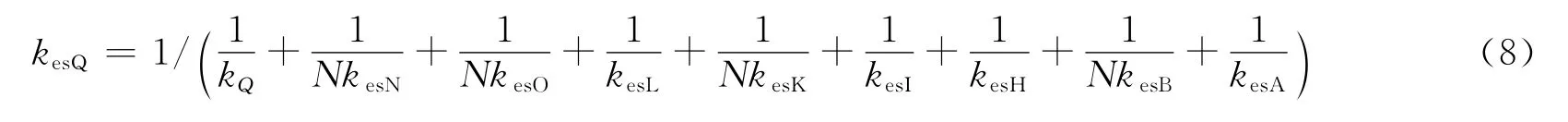
3 传动系统总刚度计算结果及分析
对于齿轮材料为不锈钢,轴系为钛合金的关节传动系统,计算表明轴的扭转刚度与齿轮扭转刚度在一个数量级内,因此计算各组刚度时应将轴和齿轮都考虑在其中。计算表1中各齿轮与轴相对于输出齿轮Q的等效刚度,如图5所示。显然,表1中序号为第1、2、5、6组的等效刚度比其他组高出许多,当这4组刚度同时降低10%~50%时,传动系统总刚度基本没变(见图6);当这4组刚度同时降低50%~80%时,传动系统总刚度略有降低;当这4组刚度同时降低90%时,传动系统总刚度仅降低1.85%,影响甚微;当超过90%时,则会引起传动系统总刚度的显著降低。故上述4组是关节减小质量的重点。
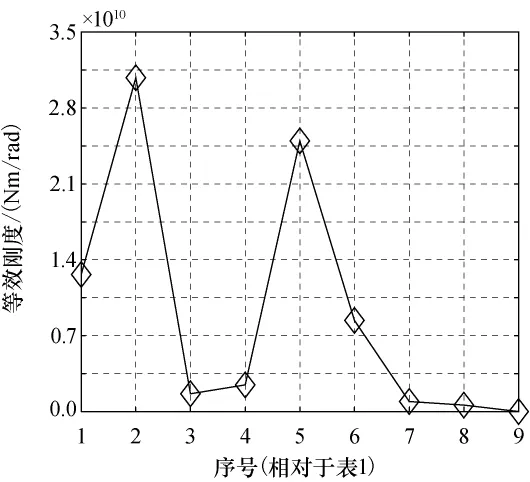
图5 各组齿轮相对于输出齿轮的等效刚度Fig.5 Equivalent stiffness of every group of gears
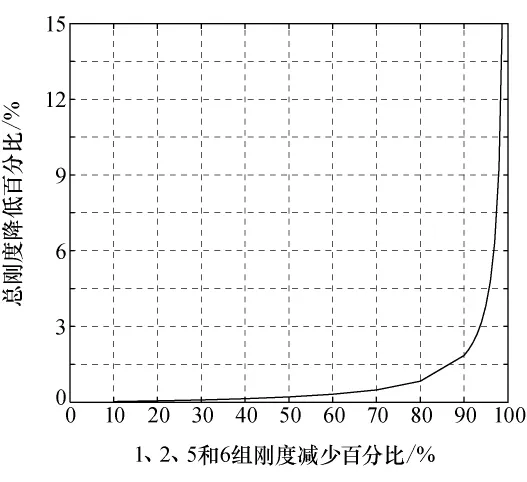
图6 1、2、5、6组齿轮刚度对总刚度的影响Fig.6 Effect of the stiffness of the 1st,2nd,5th and 6th gears on the general stiffness of the joint transmission system
由式(8)知,关节总刚度取决于各齿轮中刚度最小的。显然,高速级及中速级刚度经减速比及等效半径比的放大后,刚度明显大于低速级,则低速级轮系刚度对整个关节刚度影响较大。
由图5可知,低速级(序号第9)的输出齿轮Q的刚度ksQ远远小于其他组,其刚度增加10倍时,传动系统总刚度呈近似线性增加(见图7);当其刚度增加10~50倍时,传动系统总刚度尽管增速变缓,但仍会明显提高;当其刚度增加80倍以上时则对传动系统总刚度影响较小。齿轮扭转刚度主要取决于齿轮齿宽及齿轮半径,增加齿轮的基圆半径势必会改变其模数,从而会改变齿轮系其他的性能,因而增加齿轮宽度即可直接有效地提高整个关节刚度,改善关节性能。
由式(7)知,9组等效刚度都很接近时,总刚度最优,则应合理分配各级齿轮的减速比及等效半径比,以使得各级刚度平均分配。
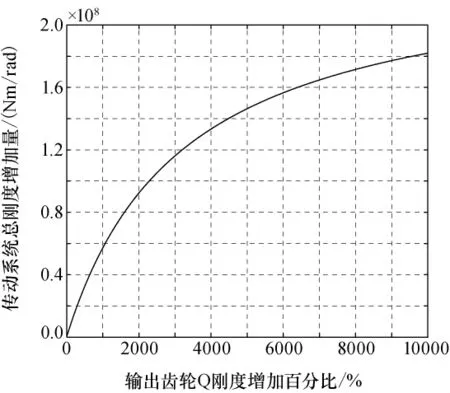
图7 输出齿轮Q的刚度对关节总刚度影响Fig.7 Effect of the stiffness of the last gear on the joint transmission system
另外,行星齿轮个数的增加对整体刚度也会有较大的影响,当将第9组齿轮刚度提高到与第8组齿轮刚度一个量级时,增加1个N级行星齿轮个数,总刚度增加19%。另外,行星齿轮个数的增加可以使齿轮受力更加均匀。
4 结束语
通过本文分析得到如下结论:
1)就本文所述关节传动系统,第1、2、5、6组对应的齿轮与轴具有较大的刚度裕度,同时降低其刚度90%时,关节传动系统总刚度仅降低1.85%,影响甚微,是关节减重的重点对象,可以通过减小齿宽等措施来减轻关节质量,但进一步降低第1、2、5、6组的刚度会显著降低关节传动系统总刚度,设计时需要权衡考虑。
2)空间多级传动的大传动比关节低速级等效刚度低于其他级等效刚度,因此,传动系统总刚度主要取决于低速级刚度,传动系统总刚度随低速级(第9组)的等效刚度的增加而近似线性增加。
3)在关节传动系统的设计时应尽量将各速度级等效刚度优化至同一量级,以达到提高刚度、减轻质量的综合效果。
4)周转轮系中行星齿轮个数的增加有利于提高关节刚度,但同时会增加传动系统的质量,设计时应权衡考虑。
[1]WOERKOM VAN P TH L M,MISRA A K.Robotic Manipulators In Space:A Dynamics and Control Perspective[J].Acta Astronautica.1996,38:411-421.
[2]NGUYEN P K,RAVINDRAN R,CAR R,et al.Structural Flexibility Of The Shuttle Remote Manipulator System Mechanical Arm [C]∥Guidance And Control Conference,San Diego,CA,Collection of Technical Papers.New York,American Institute of Aeronautics and Astronautics,1982.
[3]王龙宝.齿轮刚度计算及其有限元分析 [D].镇江:江苏大学,2007.WANG LONGBAO.Stiffness Calculation and FME Analysis of Gears[D].Zhenjiang:Jiangsu University,2007.
[4]CAHALA G.ISO 6336Vs AGMA 2001Gear Rating Comparison For Industrial Gear Applications.[C].Cement Industry Technical Conference,IEEE-IAS/PCA:19-22.1999.
[5]国家技术监督局.GB/T3480-1997渐开线圆柱齿轮承载能力计算方法 [S].北京:中国标准出版社,1997.CHINA STATE BUREAU OF QUALITY AND TECHNICAL SUPERVISION.GB/T3480-1997Calculation Methods of Load Capacity for Involute Cylindrical Gears[S].Beijing:China Standard Press,1997.
[6]张策.机械动力学 [M].北京:高等教育出版社,2007:205-206.ZHANG CE.Machinery dynamics[M].Beijing:Higher Education Press,2007:205-206.
