黄河下游河段渗漏耗水量时空变化分析
2013-11-25李红良李晓宇
李红良,李 焯,李晓宇
(黄河水利委员会水文局,河南 郑州450004)
黄河下游开展水量统一调度以来,为黄河有限水资源的合理利用和优化配置发挥了重要作用. 由于两岸引黄水量大,未控引水及自然耗水量影响因素复杂,加大了水量统一调度的难度.河道渗漏耗水量是黄河下游自然耗水量的重要组成部分. 黄河下游河段两岸大堤内外高差大,是著名的“地上悬河”,没有地下水补给河道,黄河下游河川径流向两岸大堤以外的侧渗水量即为河道渗漏耗水量. 针对黄河下游“地上悬河”的特殊地貌状况,笔者利用竖管法现场测定河床沉积物的渗透系数;以达西定律为基本数学模型,通过物理试验确定参数,把试验与数学建模相结合,开展黄河下游河道的渗漏耗水量计算,并分析黄河下游河道渗漏耗水量的时空变化特征,为黄河下游水量统一调度提供技术支撑.
1 野外现场试验及结果
1.1 野外现场试验
野外现场竖管试验能够基本反映试验现场河床沉积物的实际情况,国内外许多研究者对野外现场竖管试验进行了较深入的研究[1-2]. 采用变水头渗透试验测定含水层介质或其他孔隙介质的渗透系数已在水文地质领域得到广泛的认可和应用. 此次研究在黄河花园口河段对河床沉积物同时进行了竖管试验、变水头渗透试验,并对试验结果进行对比分析,所测得渗透系数值相对误差小于0.6%.说明两个试验的结果几乎相同,可以在黄河下游河段进行变水头渗透试验.
此次野外现场试验设在黄河下游干流花园口、高村、孙口、艾山、泺口等5 个水文站附近,选择便于开展试验的河段作为试验点和取样点,进行了为期4 d 的现场竖管试验,并在花园口站附近河段分别进行了竖管、L 状、中间有一定夹角的试验管试验,其他站附近河段仅进行了竖管试验,图1为竖管试验设计示意图.
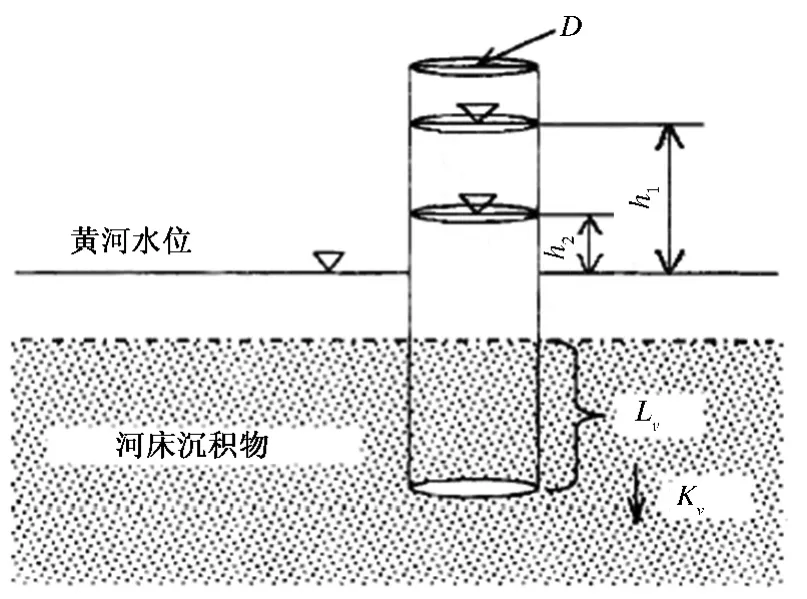
图1 渗透试验设计示意图
根据文献[1]的研究,竖管内沉积物的渗透系数可表示为
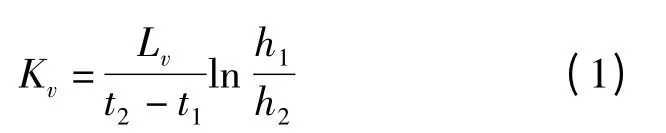
式中:Kv为垂向渗透系数,cm/s;Lv为直状试验管内沉积物长度,cm;h1,h2分别为t1,t2时刻对应的管内水位,m.
由野外现场竖管试验及线性内插得到黄河下游各水文站的河床沉积物垂向渗透系数,见表1.

表1 实测垂向渗透系数 m/d
1.2 野外现场竖管法测试渗透系数的合理性分析
1.2.1 现场试验结果与其他研究成果对比分析
由现场所取河床沉积物颗粒分析可知,黄河下游河段以细粒土为主,属于中低渗透性介质.其他研究成果中类似渗透介质的渗透系数为0. 086 ~0.864 m/d[3].该次现场试验测定的结果为0.19 ~0.71 m/d,在其他研究成果的范围内.
1.2.2 现场试验结果沿程变化分析
从表1可以看出,该次现场竖管试验所测定的渗透系数,由花园口至下游的泺口试验点,呈沿程减小趋势,这与河床沉积物的颗粒粒径沿程逐渐变细的趋势基本一致.
通过以上分析可知,该次竖管法试验所测得的河床沉积物渗透系数是合理的,符合黄河下游河道的实际情况,可以在黄河下游河段的渗漏耗水量计算中应用.
2 河道概化
黄河下游河道是举世闻名的“地上悬河”,黄河河川径流渗漏补给地下水有其独有的特性. 黄河河床横剖面概化如图2所示.图中:K1为河床沉积物的垂向渗透系数,m/d;K2为潜水含水层的垂向渗透系数,m/d;M1为河床沉积物的平均厚度,m;M2为渗入河床沉积物的河水在潜水含水层中流至长观孔的路径长度,m.

图2 黄河渗漏补给地下水概化图
黄河下游河段是“地上悬河”,两岸大堤内外的高差3 ~5 m,部分河段可达10 m.按照达西定律理论,只要有水位差存在,在重力作用下,河川径流将源源不断地渗入河道床面以下,转化为两岸大堤以外地下水,成为其主要补给源.
黄河河川径流渗漏补给堤外地下水的水量大小不仅与大堤内外地下水位的水位差有关,而且与河床沉积物颗粒及含水层的岩性有着密切的联系. 由于历年泥沙淤积的颗粒不同,所以河道床面以下沉积物呈多孔介质地层结构,为河川径流渗漏并转化为两岸大堤以外的地下水创造了相应的地质环境.
垂直于河床沉积物与含水层层面方向的等效渗透系数采用下式计算[4],
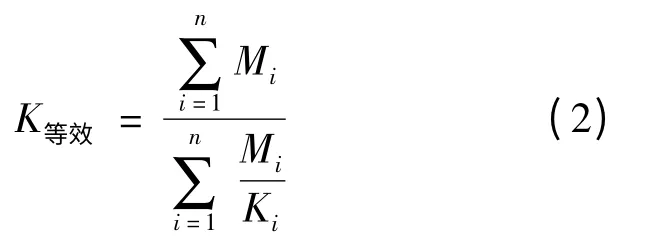
在河道不断流的情况下,渗漏补给地下水运动为饱和流运动,可利用地下水动力学的基本定律——达西定律计算黄河下游渗漏耗水量.
3 黄河下游河段河道渗漏耗水量计算与分析
3.1 计算方法
根据研究需要,按照在同一子河段内应具有河道形态基本均匀、河床沉积物基本处于同一地质单元[5],每个子河段都应包含一个干流水文站的原则,以两相邻水文站的中点断面作为子河段范围的界定标志,将花园口—利津河段分解为7 个子河段.经概化后,各子河段的河床沉积物渗透系数及长度见表2.
取两相邻水文站中点断面处附近的水位作为子河段的河道内水位,距黄河最近的长观孔的地下水位作为子河段的地下水位,中点断面实测水面宽作为子河段的水面宽,中点断面处的等效渗透系数作为子河段的等效渗透系数,根据达西定律,即可计算出子河段的渗漏耗水量,各子河段的渗漏耗水量之和即为整个黄河下游河段的渗漏耗水量.

表2 垂向渗透系数Kv 及长度概化结果
3.2 计算结果
选取研究时段为1991—2005年.在分析黄河下游自然地理、水文地质条件的基础上,采用研究时段内各水文站水位资料、两岸距离黄河较近的长观孔地下水位资料,计算各水文站点附近堤内外水位差,并将计算结果概化至各子河段,结合各子河段的长度、河床沉积物厚度、等效渗透系数等信息,应用达西定律建立河道渗漏计算模型,计算黄河下游河段的月、年渗漏耗水量.黄河下游花园口—利津河段多年平均渗漏耗水量为7.892 亿m3. 黄河下游花园口—利津河段1991—2005年各年及月均渗漏耗水量及各区间年均渗漏耗水量见表3—5.
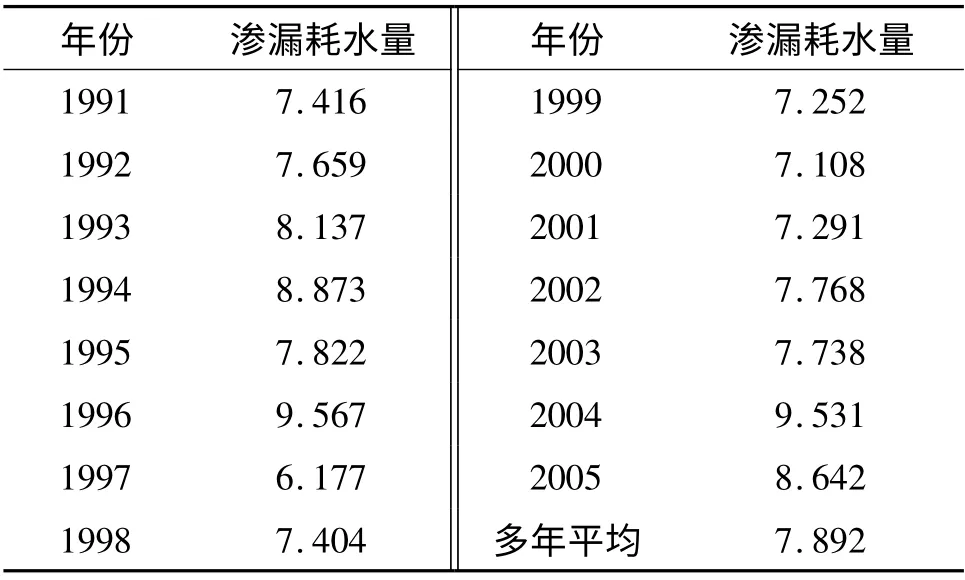
表3 花园口—利津河段各年渗漏耗水量 亿m3
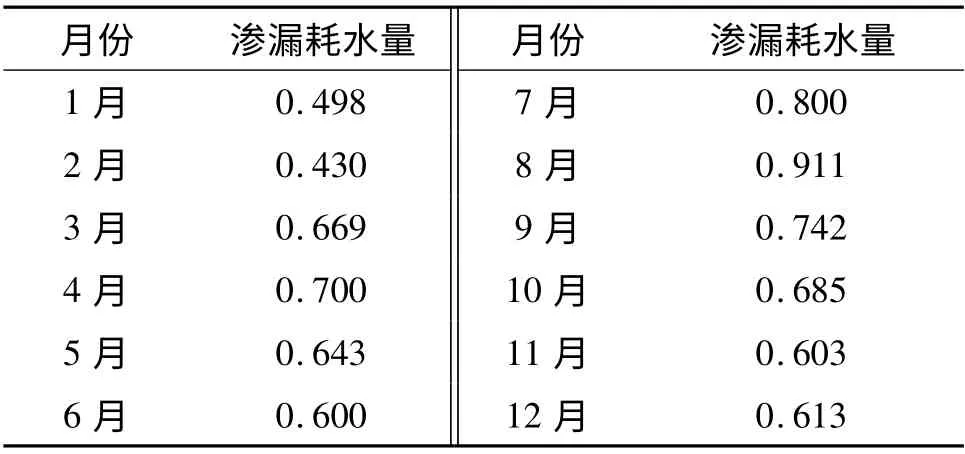
表4 花园口—利津河段月均渗漏耗水量 亿m3

表5 各区间年均渗漏耗水量 亿m3
3.3 计算结果分析
1)年际变化分析. 由表3可以看出,1996年的渗漏耗水量最大,为9.567 亿m3,1997年的渗漏耗水量最小,为6.177 亿m3,最大为最小的1.55 倍,年均渗漏耗水量为7.892 亿m3. 研究时段内,花园口站实测年均径流量为233.37 亿m3,说明下游来水量的3.38%消耗于渗漏水量.由于下游河道水量除蒸散发与渗漏耗水外,还有人类活动因素的影响,因此,尽管花园口站实测径流量与下游渗漏耗水量的年际变化过程相对应,但并不完全一致.由于黄河下游河道沉积物及含水层的岩性对渗漏耗水量影响不大,渗漏耗水量主要受来水量的影响.当来水量变化不大时,人类活动因素的影响将导致河道水量减少,下游年渗漏耗水量将会发生变化.
2)年内变化分析.由表4可以看出,1991—2005年黄河下游8月份的平均渗漏耗水量最大,为0.911 亿m3,占年均值的11.5%;2月份的平均渗漏耗水量最小,为0.430 亿m3,占年均值的5.5%. 最大月均渗漏水耗量是最小的2.12 倍.黄河下游8月份月均来水量为32.27 亿m3,是来水最丰的月份,其渗漏耗水量也最大. 尽管月均来水量1月份为10.67 亿m3,是来水最枯的月份,但是,2月份两岸工农业引水比1月份明显加大,导致沿程进入下游河道的水量减少,这是2月份渗漏耗水量为最小的主要原因.在来水较枯的月份,人类活动是渗漏耗水量发生变化的主要因素.
3)黄河下游河段各区间年均渗漏耗水量沿程变化分析.由表5可知,在下游各区间的年均渗漏耗水量中,花园口—夹河滩区间达到3.303 亿m3,为最大值.这是因为泥沙进入黄河下游宽浅游荡性河段以后,粗颗粒泥沙绝大部分淤积在该区间,河床沉积物颗粒粗,孔隙率较大,为渗漏提供了有利的条件.越向下游,河床沉积物颗粒越细,孔隙率越小,越不利于渗漏,泺口—利津区间年均渗漏耗水量最小,仅为0.248 亿m3.最大区间年均渗漏水量是最小的13.3 倍.
4)黄河下游水量调度省际断面上下游变化分析.高村水文站为黄河下游水量调度省际断面,由表5可知,花园口—高村区间年均渗漏耗水量为5.126 亿m3,占花园口—利津区间多年平均值的65.0%,也就是说,黄河下游河段的渗漏耗水量主要发生在花园口—高村区间.
5)断流影响分析. 前期长时间的断流,造成堤外地下水位下降,当汛期河道内有水流通过时,就会加大河道内水位与大堤以外地下水之间的水位差.若汛期来水量较丰,渗漏耗水量较常年偏多;若汛期来水量较枯,渗漏耗水量就会较常年偏少.
1996年利津站断流时间共计136 d,当年汛期来水量丰沛,花园口站实测年径流量277.3 亿m3,虽然1996年下游断流相当严重,但渗漏耗水量仍为最大.
1997年是黄河下游有资料记录以来断流最严重的一年,利津站断流226 d,断流河段长度占花园口以下河长的91%左右.花园口站实测年径流量仅为103.4 亿m3,汛期来水量枯,所以1997年渗漏耗水量最小.
4 结 语
1)在黄河下游,花园口、高村、孙口、艾山、泺口等水文站附近采用竖管进行河床沉积物渗透系数现场测定,其结果分别为0. 71,0. 29,0. 34,0. 19,0.24 m/d.
2)黄河下游8月份的平均渗漏耗水量最大,为0.911 亿m3;2月份的平均渗漏耗水量最小,为0.430 亿m3;月均最大渗漏耗水量是最小的2. 12倍.1996年渗漏耗水量为9.567 亿m3,是最大值;1997年年渗漏耗水量为6.177 亿m3,是最小值;最大年渗漏耗水量是最小的1.55 倍.多年平均渗漏耗水量为7.892 亿m3.
3)渗漏耗水量沿程有减少趋势. 上游花园口—夹河滩区间年均渗漏耗水量最大,达3.303 亿m3;下游泺口—利津区间年均渗漏耗水量最小,为0.248 亿m3;最大区间年均渗漏耗水量是最小的13.3 倍.
4)按黄河下游水量调度省际断面分析,渗漏耗水量主要产生在花园口—高村区间,年均渗漏耗水量5. 126 亿m3,占花园口—利津区间年均值的65.0%.
[1]Chen X H.Measurement of streambed hydraulic conductivity and its anisotropy[J].Environmental Geology,2000,39(12):1317-1324.
[2]迟宝明,束龙仓.张家港暨阳湖湖底沉积物渗透系数的现场测定[J]. 吉林大学学报:地球科学版,2003,33(4):539-540.
[3]王志华.黄河下游渗漏补给地下水水量研究[D].南京:河海大学,2007.
[4]薛禹群.地下水动力学[M].北京:地质出版社,1997.
[5]秦学林.傍河取水型水源地河水诱导补给量计算方法探讨[J].电力勘测,1995(4):8-14.
