海伦方程矩量法分析＊

刘建厂

（海司信息化部 北京 100841）

1 引言

人们把用基函数和权函数将积分方程离散化为矩阵方程的数值计算方法称为矩量法［1］，矩量法是一种非常普遍的概念，其基本思想是将一个泛函方程化为矩阵方程并求解该方程。该方法在天线领域应用广泛，上世纪60年代，哈林登（Harrington）首先将矩量法应用于电磁场领域［2］。对于辐射问题，是将含有未知电流的积分方程化为矩阵方程，通过求解该矩阵方程得到天线上的电流分布。

在矩量法的分析过程中，积分方程有多种，比如双位积分方程、海伦（Hallen）积分方程、波克林顿（Pocklington）积分方程、反应积分方程等［3～7］。本文重点对海伦积分方程的矩量法求解过程进行了研究，文中详细推导了海伦积分方程，分别选取全域基和分域积进行了分析，尤其对脉冲分域积、δ权函数进行了重点研究，特别是匹配点的选取和广义阻抗矩阵的特性。

2 海伦积分方程［1～8］

海伦积分方程是基于Δ间隙电压源［5］求解对称偶极子天线的，如图1所示偶极子天线半径为a，长度为L，沿z轴放置于坐标原点，使用间隙为Δ（Δ无限小）强度为Eg的电压源激励。

假设a≼λ，a≼L，偶极子天线表面的电流仅有轴向分量，即z分量，所以沿偶极子表面电流均匀分布，并且偶极子天线端面电流为零。这样矢量位仅有轴向分量Az，于是电场表达变为Ez＝-jωAz-，根据洛仑兹（Lorentz）规范［9］，可以得出：

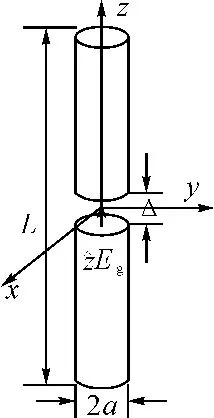
图1 偶极子天线

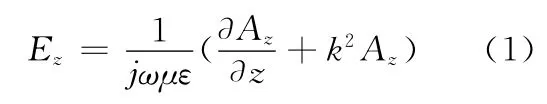
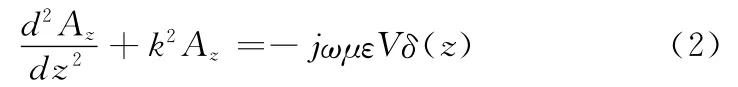
该微分方程的通解为Az＝Bcoskz＋Dsinkz，由偶极子天线的对称性可知：Az（-z）＝Az（z），所以D＝0，上面的通解变为Az＝Bcoskz，而特解可以写作：

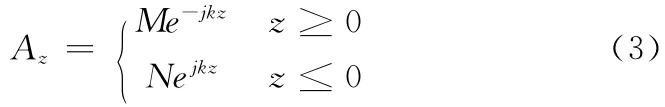
在z＝0的Δ（Δ→0）邻域对方程（2）两边求积分：

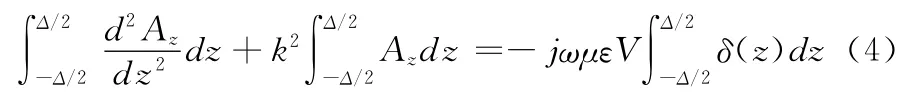
由于Az在z＝0处连续，故，上式变为

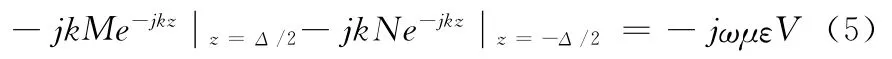
Δ→0时，可得：-jk（M＋N）＝-jωμεV，即：M＋N，根据Az在z＝0处连续这一条件，可得M＝N。故微分方程（2）的特解为

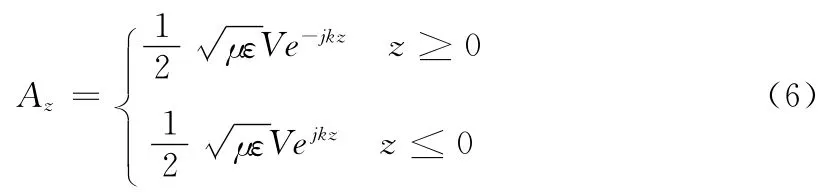
Az＝，即：

Az＝Bcoskz＋B′Ve-jk｜z｜，式中，

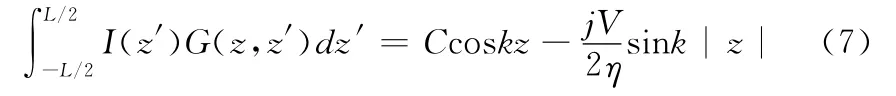
3 海伦积分方程矩量法求解

用矩量法求解海伦积分方程时，一般使用全域基、点匹配法，对于细偶极子天线，由于已知电流分布接近正弦分布，所以经常采用正弦分布的全域基函数，这样使解的收敛性很好，用2～3个展开函数便能较好的逼近未知函数。而使用分域基求解由于涉及到偶极子天线的分段和匹配点的选取，所以解法不是很统一，虽然有文献中使用分域脉冲基、点匹配法进行分析，但偶极子天线的分段和匹配点的选取不是很理想，特别匹配点与分段重合的情况，计算广义阻抗矩阵易出现奇异点。

3.1 全域基、点匹配［7］

对于图1所示偶极子天线，选用三角全域基函数展开，待求电流可表示为

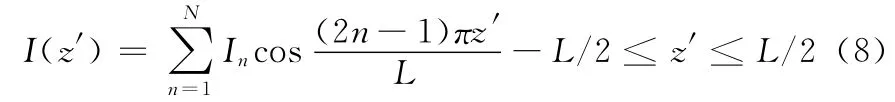
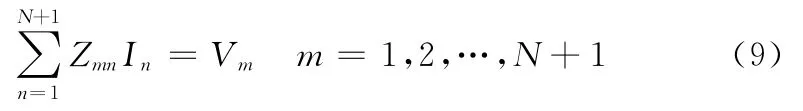
其中：

求解出系数In后，可以得到天线的输入阻抗：

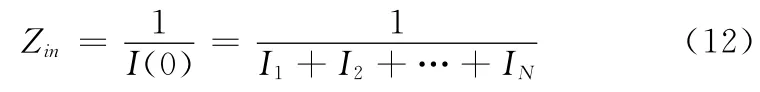
由于天线在远场区只有Eθ分量，故：

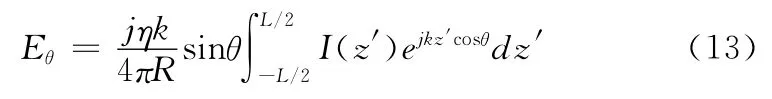
通过进一步计算，可以求出功率方向图：

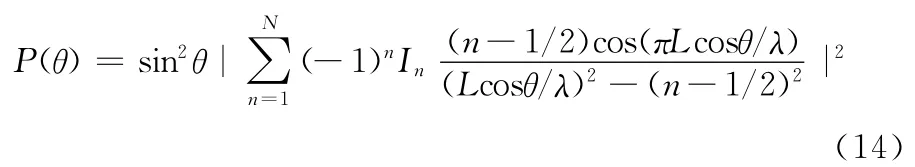
3.2 分域基、点匹配［2～3，5］

选用分域脉冲基函数作为展开函数，采用点匹配法，脉冲基函数选为

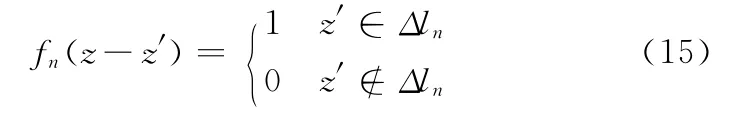
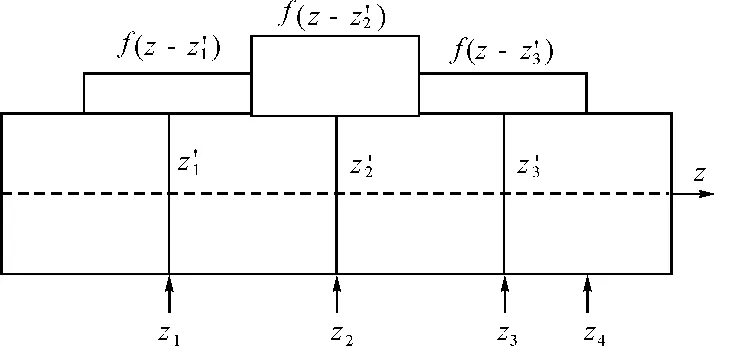
图2 天线分段情况和匹配点选取示意图

本文采用的分段和匹配方法是将天线分为偶数段，展开脉冲函数数目为奇数，偶极子天线两端各留半个分段，匹配点选在每个脉冲的中心，保证在馈电处有一个匹配点。因为方程有N＋1个未知量，故在天线端点处的一个分段中点还需再选一个匹配点，这样选取的好处是可以使偶极子天线末端的电流为零，具体情况见图2。离散后的N＋1阶线性方程组表示为

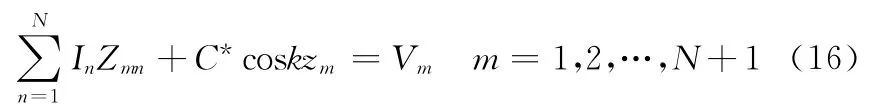
式中：

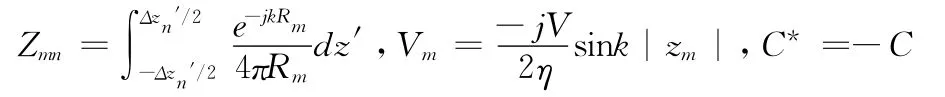
则矩阵形式的表达式为

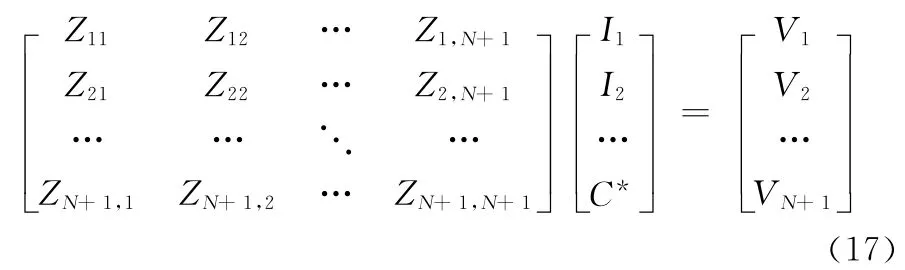
即：ZI＝V，进一步可得：I＝Z-1V，I的最后一项是系数C＊，在后面计算中不再使用，这样便得到了电流分布，进而可以求出辐射场。

偶极子的辐射场在远区只有Eθ和Hφ分量，经过化简，偶极子的第n段的远区辐射场为

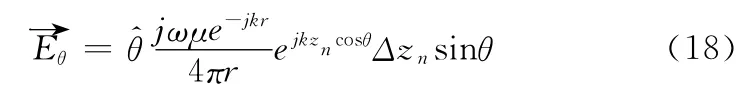
偶极子天线的增益：

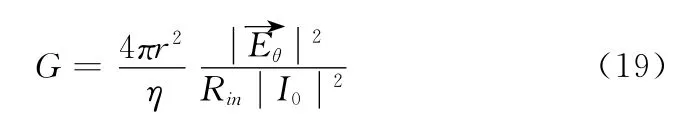
式中，I0表示馈电点的电流。

4 数值计算

对L＝0.5λ，a＝0.0001λ和a＝0.001λ中央单位电压馈电的偶极子天线，天线放置情况如图1所示，分别用三角全域基、点匹配和脉冲分域基、点匹配进行了矩量法分析。

4.1 电流分布

全域基采用的基函数个数为3，匹配点是在L／2 上等间距取N＋1个点；分域基的天线分段数为60，即采用59个脉冲基函数，匹配点选在每个脉冲的中心，另在天线的端点处的分段中心再取一个匹配点。

当偶极子半径a＝0.0001λ时，使用全域基与分域基得到的电流分布一致性很好，如图3所示；而当偶极子的半径增大到a＝0.001λ时，使用分域基得到的电流分布与使用全域基得到的电流分布产生了一定的偏差，特别是在馈电点处，如图4所示。

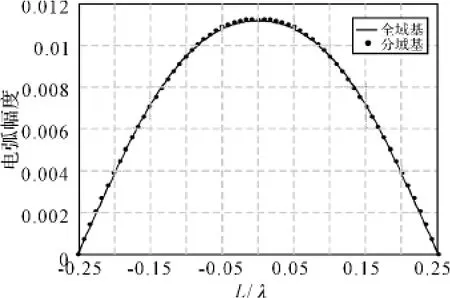
图3 a／λ＝0.0001偶极子的电流分布

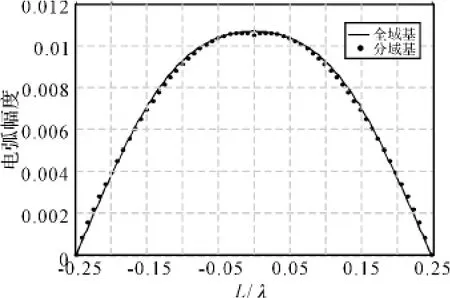
图4 a／λ＝0.001偶极子的电流分布

4.2 辐射特性

功率方向图对偶极子天线半径变化的敏感度要低一些，在偶极子半径a＝0.0001λ时，使用全域基和分域基得到的E面功率方向图如图5所示，两种方法所得结果吻合度很好。

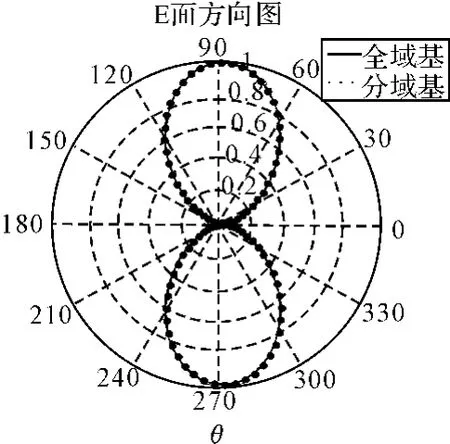
图5 偶极子的E 面功率方向图

4.3 输入阻抗与增益系数

偶极子半径a＝0.0001λ时的输入阻抗和增益系数结果如表1所示，偶极子半径a＝0.001λ时的输入阻抗和增益系数结果如表2所示。

表1 a＝0.0001λ时的输入阻抗与增益系数

表2 a＝0.001λ时的输入阻抗与增益系数

计算结果表明：采用全域基、点匹配法时，N值不宜取的过大，一般取N＝2～3即可，N值过大，会使阻抗矩阵产生病态；采用脉冲分域基、点匹配法时，偶极子的分段情况和匹配点的选取尤为重要，虽然不同的选取方法大致都能得到较为理想的结果，但在细节上，比如阻抗矩阵的条件数等方面还是存在很大差距。

两种方法在求解偶极子辐射特性方面差别不大，功率方向图的结果比较一致；对于线径较大的偶极子天线，全域基比分域基给出的电流分布结果更加稳定；输入阻抗和增益系数方面，全域基也比分域基的情况要好一些。

5 病态矩阵［5，7，10］

使用全域基、点匹配方法，在偶极子线径较小时，对基函数的项数N感度不是很大，不同N值对阻抗矩阵条件数的影响不大，但随着偶极子线径的增加，阻抗矩阵的条件数对N值的敏感度增强，此时，如果N取得过大，会使阻抗矩阵Zmn变为病态，条件数随着N的增加不断变大，导致电流分布产生畸变。a＝0.005λ的半波偶极子天线随N值的变化电流分布如图6～7所示。

图6 N 为3、5、7、9时的电流分布

图7 N 为3、11、13、15时的电流分布

全域基、点匹配法阻抗矩阵的条件数随N的变化见表3。分域基、点匹配法得到的阻抗矩阵条件数在偶极子线径较大时，随分段数的增加，变化更为剧烈，更容易使阻抗矩阵产生病态。

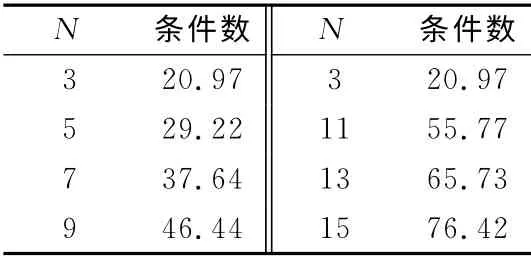
表3 阻抗矩阵的条件数

6 结语

海伦积分方程是天线矩量法研究中的一种重要方程，在实际应用中，采用不同的基函数和权函数，对数值计算结果有一定影响。本文详细推导了海伦积分方程的建立过程，分别采用全域基和分域基对偶极子天线进行了矩量法分析，实现了一种新的分段和匹配方法，并对计算过程中阻抗矩阵的性态进行了分析研究，下一步工作的重点是对病态矩阵的产生原因做进一步分析。

［1］钟顺时.天线理论与技术［M］.北京：电子工业出版社，2011：54-55＋465.

［2］HARRINGTON R F.计算电磁场的矩量法［M］.北京：国防工业出版社，1981：11-95.

［3］刘其中，宫德明.天线的计算机辅助设计［M］.西安：西安电子科技大学出版社，2004：95-111.

［4］李世智.电磁辐射与散射问题的矩量法［M］.北京：电子工业出版社，1985：25-47.

［5］STUTZMAN W L，THIELE G A.天线理论与设计［M］.北京：人民邮电出版社，2006：402-409＋424.

［6］宋铮，张建华，黄冶，等.《天线与电波传播（第二版）》学习指导［M］.西安：西安电子科技大学出版社，2011：174-177.

［7］王世锦，陈代宗，冀秀芹.天线微波程序集［M］.北京：宇航出版社，1989：73-79.

［8］卢万铮.天线理论与技术［M］.西安：西安电子科技大学出版社，2004：97-98.

［9］康行健.天线原理与设计［M］.北京：北京理工大学出版社，1993：9＋42.

［10］高粱，王运行，张德存.矩量法求解海伦方程中的病态现象［J］.海军航空工程学院学报（军事版），2011，9（4）：98-100.

［11］姜光兴，曹伟，朱洪波.基于不同积分方程的线天线矩量法分析［J］.南京邮电大学学报，2005，25（1）：46-50.

［12］KING R，C W HARRISON，Jr.The Distribution of Curr-ent Along a Symmetrical Center-Driven Antenna［J］.Proc IRE，1943，31：548-567.

［13］Mei K K.On the Integral Equations of Thin Wire Anten-nas［J］.IEEE Trans on AP，1965，13：374-378.

［14］NERI R.Input Impedance of Thin Dipoles by Moment Method［J］.Electronics Letters，1979，15（14）：418-420.