分布式多传感器无源定位综述＊

李建春 刘方正 章四兵

（电子工程学院 合肥 230037）

1 引言

分布式多传感器无源定位可分为分布式多传感器辐射源定位和分布式多传感器外辐射源定位。分布式多传感器辐射源定位主要是多个传感器利用目标自身所辐射的信号进行定位。如图1所示，其基本原理是多个接收传感器分散配置，接收辐射源目标发射的电磁信号，接收传感器通过分析、处理，提取目标的方位、时差、频差等参数，实现对辐射源目标的定位和跟踪。该定位体制接收传感器分散部署，可提取方位、时差、频差等多类参数，同时不辐射电磁波，因而其定位精度较高，同时具有“四抗”（抗干扰、抗反辐射导弹、抗低空突防和反隐身）能力。分布式多传感器外辐射源定位则是多个传感器利用第三方辐射源的信号（如民用的电视、广播、通信、卫星，以及手机基站等民用辐射源等）照射到目标后的反射信号进行定位。该定位体制可看作特殊的多基地雷达系统，如图2所示，基本原理是利用目标反射第三方辐射源的发射信号实现对目标的定位及跟踪。该定位体制收发分置，故它具有定位精度较高及“四抗”能力等优点。

2 分布式多传感器无源定位的特点

分布式多传感器无源定位的特点主要表现在：1）不主动辐射电磁波信号，具有非常强的隐蔽性，生存能力强；2）系统成本较低，整个系统没有发射模块，只有接收装置，故可以节省大量经费；3）多个接收传感器可以大范围分散部署，通过拉大站间基线长度，既可以提高定位精度，又可以扩大探测覆盖区域；4）多个接收传感器可以采用不同的搜索频段，可以大大提高发现目标的概率，包括隐身目标；5）对于采取电磁静默措施的目标，分布式多传感器外辐射源定位体制可以利用第三方辐射源的机会照射，实现对目标的检测、参数测量、定位及跟踪。

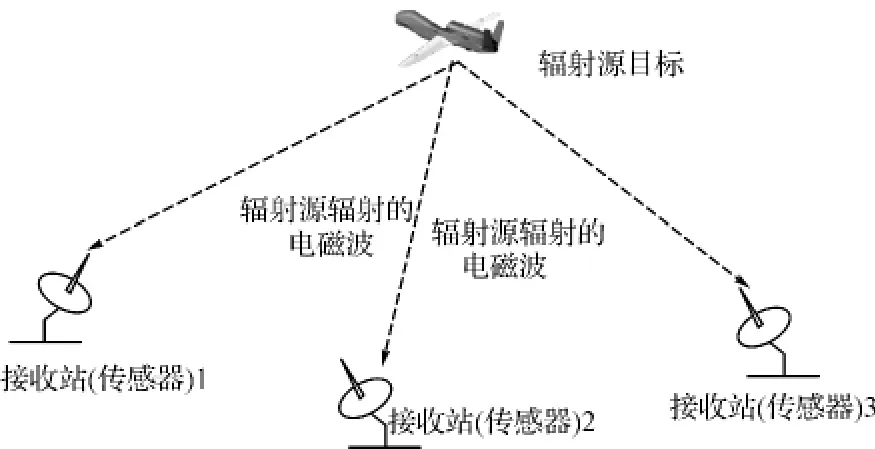
图1 分布式多传感器辐射源定位示意图

3 相关研究现状

3.1 分布式多传感器辐射源定位的研究状况

分布式多传感器辐射源定位在民用和军事应用方面都得到了迅猛的发展。大多数国家都对尤其是西方发达国家的跨国公司，比如Motorola、Nokia、Ericsson等积极地开展对基于GSM、IS-95和第三代移动通信系统的定位技术的研究，并且制定了相应的实施方案及行业标准（如GSM系统中选用的增强观测时差（E-OTD）定位法；WCDMA 系统中选用OTDOA-IPDL定位法［1］。）同时分布式多传感器辐射源定位在军事应用上也已研制出了许多装备［2］。俄罗斯的“MCS-90系统”是一个由三接收站构成的无源探测系统，利用时差定位原理实现对目标的定位及跟踪。乌克兰的“卡拉秋塔”系统，它有单站、三站两种结构形式，单站系统主要用来探测对方无线电信号，对所截获的信号进行分析、识别，在其构建的防空体系中担负早期预警任务，三站系统可对600km 内的低空目标进行定位并且可标绘其航迹。捷克的“TAMANA”系统是三站时差定位系统，可对空中、地面和海面目标进行定位、识别与跟踪，并可以实时提供目标点迹、航迹。其各站的基线长度为10km～35km，探测距离大于400km。捷克的“VERA-E”系统，在较宽的频带范围内处理各种辐射源电磁波信号，“VERA-E”系统由适当部署的三接收站或四接收站组成，采用时差定位技术来确定目标的位置，是目前比较成熟和实用的分布式无源定位系统。以色列的“EL／L-8388”对空早期预警系统，采用短基线时差定位体制，工作频段0.5GHz～18GHz，其时差估计精度最高可达1ns。

图2 分布式多传感器外辐射源定位示意图

3.2 分布式多传感器外辐射源定位的研究状况

分布式多传感器外辐射源定位系统主要有［3］：法国国家航空研究局以巴黎的埃菲尔电视台广播信号作为外辐射源信号，构建了非合作无源雷达试验系统；德国西门子公司利用民用电台信号作为外辐射源信号，构建了无源雷达试验系统；英国防御研究局利用电视音频调幅载波信号作为外辐射源信号，构建了无源雷达试验系统；较为成熟的系统是美国洛克希德·马丁公司利用调频广播信号和电视信号作为第三方辐射源信号的“沉默哨兵”分布式无源探测定位系统。“沉默哨兵”系统的工作原理［4］：利用商业调频电台和电视台发射的50MHz～800MHz连续波信号，检测、跟踪、监视任务区内的运动目标。该系统由大动态范围数字接收机、相控阵接收天线、高性能并行处理器及相关软件组成。该系统能够跟踪到180km～220km 的反射面积为10m2的目标，并且能同时跟踪200个以上目标，分辨率为15m。该系统有120°的观察范围，采用数字波束形成技术实现整个扇区覆盖，可跟踪固定翼飞机、旋翼机、巡航导弹和弹道导弹。系统的核心是“无源相控定位技术”，系统自身不辐射电磁波，这种静默的工作模式使得系统可以躲避对方的侦察装备和反辐射导弹，保证了自身安全。

4 分布式多传感器无源定位的关键技术

4.1 分布式无源定位技术

在分布式无源定位技术中，直接根据接收的辐射源目标信号（无需参数估计）得出目标位置，该方法称为直接定位法［5］，也可首先对辐射源目标信号进行参数估计，然后利用相关参数（到达时间、频率等）对目标位置进行估计，该方法称为两步定位法［6］。

基于参数估计的两步定位技术可以分为种，一种是基于数据库的映射方法，该类算法需在定位之前的训练阶段建立所需要的数据库［7］；另一种是基于几何或统计的方法。其中基于数据库定位技术的计算量比较大，不具备实时性。一般工程上都采用基于几何或统计的定位方法。几何定位方法先利用单一或多个测量参数确定出定位曲线或曲面，再通过计算多条定位曲线或曲面的交点来确定目标的坐标。例如，由TOA 参数得出的距离信息，可以确定的定位线为一个圆或球。对于TDOA 参数而言，每个测量参数对应一条双曲线或双曲面，确定双曲线或双曲面的交点即完成目标位置的估计。几何定位方法可以应用于混合系统，如TDOA／AOA［8］和TOA／TDOA［9］等。但是在几何定位方法中认为所有测量参数均为真实值，因此多条定位线或面才会相交于一点。然而在实际情况下，所有的量测参数均叠加了噪声，噪声属于随机误差，因此多条定位线或面实际上相交于某一个区域。相比较而言，统计定位方法则具有更广的适用范围［10］。所谓统计定位方法，即根据量测参数、误差的先验误差模型建立代价函数，如测量方程或似然函数，然后利用贝叶斯或最大似然进行处理［11］。

直接定位是一种通过建立代价函数，采用二维平面搜索直接解算出信号中包含的目标位置信息的方法。该方法避免了传统定位法两步定位的缺陷，且不要求传感器间的时间同步，但现有工作在研究时仅考虑了目标传送信号到传感器的信道衰减及干扰，而忽视了由传感器传送信号到另一传感器（或定位中心）这一过程的影响，且直接定位算法的计算复杂度远远高于两步定位技术。

4.1.1 AOA（Angle Of Arrival）技术

AOA 是使用阵列天线来估计信号到达方向对目标位置进行估计。一个AOA 测量值可以确定目标辐射源的一个角度方向，如果至少有两次不同地点的有效测量，则辐射源的位置就可以利用两个角度方向相交确定出来。通常，可以利用多个地点的AOA 测量值来提高测量的精度。AOA 方法虽然原理简单，但它存在一定的缺陷，为了得到精确的AOA 估计，关键的一点就是信号从发射点到天线需是LOS（Line Of Sight）传播，因此对于非视距NLOS（Non Line Of Sight）信道存在一定困难。AOA 的测量设备都是多天线系统，各通道之间的一致性要求很高，设备不但昂贵而且笨重。而且AOA 估计算法的复杂度较高，用于测量、储存、处理等会占用过多的软硬件资源。

4.1.2 TOA（Time Of Arrival）技术

TOA 是通过测量辐射源目标和接收机之间的绝对到达时间实现对目标的定位。将信号的时延乘以光速得到辐射源目标与接收机之间的距离，测量该辐射源目标和多个接收机之间的距离得到定位方程组，则辐射源目标位于以接收机为圆心，目标与接收机之间的距离为半径的圆上。TOA 定位的实现要求辐射源与接收站之间严格时间同步，以求得辐射源信号的绝对到达时间。

4.1.3 TDOA（Time Difference of Arrival）技术

TDOA 是测量辐射源目标到不同接收站之间的到达时间差而进行定位的。为了测量信号的到达时差，各接收站之间必须精确同步。TDOA 值可以定义一条以两个基站为焦点的双曲线，目标辐射源就位于双曲线上。在TDOA 定位算法研究方面，目前已提出多种具有不同精度和计算复杂性的定位算法［1］，如Fang算法、SX 和SI算法、Friedlander算法、分类征服、DAC 算法、采用两步WLS 的Chan 算法、泰勒级数展开法、近似最大似然估计（AML）算法［12］等，其中以Chan算法、泰勒级数展开法和AML 算法精度最高。Chan算法是一种具有解析表达式解的非递归的双曲线方程组解法，该算法的特点是计算量小，适合于三传感器及多传感器，在噪声较小且服从高斯分布的情况下，定位精度高。但在TDOA 测量误差较大或在一定的几何布局下，Chan算法的定位精度会显著下降。泰勒级数展开法是一种需要初始位置的递归算法，该算法的特点是能适用于各种信道环境，在初始估计位置与实际目标位置接近的情况下，定位精度高，但是在初始位置选择不好或者一定的几何布局下，算法有可能不收敛。结合Chan算法和泰勒级数展开法各自的长处，将它们融合在一起，先用Chan算法求取目标辐射源初始位置，然后在此初始位置基础上通过泰勒级数展开法得到精确估计位置［13］。Y.T.Chan最新提出了AML定位算法，其文中的仿真结果验证了此算法接近最优，在不同几何布局条件下定位精度能达到克拉美罗下限，但由于也需要多次计算，所以计算量也较大。

4.1.4 FDOA（Frequency Difference of Arrival）技术

FDOA 技术是通过测量各接收机之间所接收信号的多普勒频率差来进行定位的。其常应用于卫星对地观测定位上，因为除了地球同步卫星以外，其它的卫星相对地球上的物体是有相对运动的，这样辐射源信号到达各颗卫星时就会产生多普勒频移，又由于卫星位置不一样所以这些多普勒频移是不一样的，则形成了FDOA。每一个FDOA 在三维空间将对应于一个曲面，各个FDOA 曲面的交点就是目标辐射源的定位位置。

4.1.5 混合定位技术

这种方法是利用上述两种或者多种不同类型的信号特征测量值来实现定位，如TOA／AOA、TDOA／AOA、TDOA／TOA 等组合进行定位估计。

4.1.6 概率定位技术

从概率的角度出发，将4.1.1节到4.1.5节的参数量测方程，看作求解辐射源位置落在空间中概率最大的点或区域。在三维空间中，每一个方位角或俯仰角测量值确定一个平面，每一个TDOA 测量值确定空间中一对以两站为焦点的双曲面。由于现实中存在测量误差，可以将定位问题视为位置估计问题。既然是位置估计问题，那么就要考虑概率分布。显然，辐射源的位置估计的概率分布不为均匀分布，如果测量值是方位角或者俯仰角，那么目标位置估计落在一个平面上的可能性比落在其它区域的可能性要大一些，如果测量值是TDOA，那么目标估计值落在一个双曲面上的可能性比落在其它区域的可能性要大一些。多个角度（方位角、俯仰角）、TDOA 测量形成了多个子集，假定多次测量相互独立，那么目标可能从某个位置辐射信号的概率为多次测量所对应的概率之积。结合辐射源高度信息，那么概率之积最大所对应的位置就是目标的位置估计。

4.1.7 直接定位技术

传统的定位技术（4.1.1节到4.1.6节）要先估计TOA、AOA 和TDOA 等测量参数，然后利用几何关系计算辐射源目标的位置，其定位精度取决于第一步参数测量的精度和第二步位置解算算法的性能，在测量TOA 时还须保证多传感器间的时间同步。为克服传统两步定位方法的困难，近年来Anthony J Weiss提出了无需测量参数估计的直接定位方法［14～15］。直接定位是一种通过建立代价函数（cost function），采用二维平面搜索直接解算出信号中包含的辐射源目标位置信息的方法。该方法避免了传统定位法两步定位的缺陷，且不要求传感器间的时间同步，但现有工作在研究时仅考虑了辐射源目标传送信号到传感器的信道衰减及干扰，而忽视了由一个传感器传送信号到另一个传感器（或定位中心）这一过程的影响，因而直接定位技术的计算复杂度要远高于传统定位技术。

4.2 非线性滤波技术

单纯利用分布式多传感器无源定位技术不足以获取运动目标连续的位置信息，对于运动目标而言需要进行有效的跟踪滤波。大多数无线传感器的测量数据与目标状态间常呈非线性关系。如果利用观测数据完成目标状态的更新，必须解决非线性滤波问题。解决非线性滤波问题的方法主要分为两类，一类是将非线性问题线性化，即对高阶项采用截断或逼近的方法；另一类则是利用采样的方法来近似非线性分布。

Anderson和Moore就利用上述思想将Kalman滤波推广到非线性滤波的场合，提出了扩展卡尔曼滤波（EKF），并得到了广泛的应用。EKF 算法不再是按照某个指标去进行优化的优化算法，其性能很大程度上取决于非线性的复杂程度。因此，若非线性函数的泰勒级数展开式的高阶项较大，无法忽略的时候，线性化所导致的误差会很大，从而影响滤波的性能。针对上述存在的问题，有学者改进了EKF算法（如高阶截断EKF、迭代EKF［16］等）。相比较非线性函数的线性化近似非线性函数的概率分布要更加容易，其中UKF 和PF 是两种最具有代表性的方法。Juher等人提出的无迹卡尔曼滤波（UKF）算法［17］以UT 变换为基础，以Kalman滤波为框架，使用确定性采样获取非线性函数的概率分布。相比较EKF算法，UKF具有如下优点：对非线性函数的概率密度进行近似，而不是非线性函数的近似；非线性分布统计量的计算精度至少达到2阶；不需要计算雅可比行列式，且运算量与EKF 同阶；可以处理非加性的噪声以及离散的系统。目前，UKF被广泛应用于机器人自主定位、地面车辆导航和跟踪等。粒子滤波算法（PF）［18］是近年来兴起的最优非线性滤波方法，其通过随机采样策略，对状态空间直接进行采样，获取相互独立的随机粒子来表征后验概率密度，继而利用新的观测对后验概率密度进行更新。为了进一步提高粒子滤波算法的性能，一系列的改进算法被相继提出，如序贯重点采样算法、重点采样重采样算法SIR 和SIR-MCMC［19］等。

4.3 数据关联技术

分布式多传感器无源定位技术为实现多目标的可靠跟踪，则需要首先完成数据的可靠关联。多维分配算法是实现数据关联的一类重要手段。多维分配算法主要包括2-D 分配算法和S-D分配算法［20］。其中2-D分配算法用于解决“观测值一航迹”间关联的问题；而S-D 分配算法则处理多传感器观测数据间的“观测值一观测值”关联问题。对于2-D 分配问题而言，常用的解法包括拍卖算法，JVC算法，以及用于网络流量的Relax方法。其中，拍卖算法在目标稀疏的场景下速度比JVC算法快，但是在目标较为密集的场景中，JVC算法的性能则要优于拍卖算法。与2-D分配问题相类似，SD分配问题是一个NP-Hard问题。利用其它NP-Hard问题次优解的方法，如贪婪消源法，模拟退火法等，求解S-D分配问题的次优解，会存在大量错误的关联结果。Deb［21］，Poore［22］以及Pattipati［23］提出了一种具有可量化精度的快速多层拉格朗日解法。该方法将S-D 分配问题化简为一系列的2-D分配问题进行求解，将多维优化问题引入S-D分配算法中，提出了多传感器广义S-D 分配算法，该方法利用最大似然的方法，避免了穷举搜索，提高了分配算法的运算效率。

另外，可应用后验概率贝叶斯方法解决“观测值—航迹”间关联的问题，如联合概率数据关联法（JPDA）［24］、多假设跟踪（MHT）和概率多假设跟踪（PMHT）［25］等，上述方法具有计算量小、性能好等优点，且易于工程实现，因而备受研究人员的亲睐。近些年来，越来越多的研究将其它数学工具应用于数据的关联，从而产生新的配对算法，如聚类方法［26］，Viterbi数据关联算法（VDA）等。对于数据分配算法而言，计算的瓶颈不在获得次优数据关联的计算，而在于关联算法的运算量，因此对于数据关联算法的研究主要表现在两方面，一方面是将新的数学理论引入数据关联中，如证据理论和随机集理论等［28］，从而摆脱传统的贝叶斯理论框架；另一方面则是提高数据分配算法的计算效率，降低算法的复杂程度。

5 结语

分布式多传感器无源定位不仅可以有效地抗击电子干扰、隐身技术、反辐射武器等威胁，而且具有精度高、覆盖空域广、能对付宽带低谱密度信号等优点，使其在军事、为移动台提供定位服务、无线电监测定位上都具有巨大应用潜力。因此，在未来的战争或复杂条件下的目标定位跟踪及识别中，分布式多传感器无源定位技术将会得到越来越广泛的发展和应用。

［1］范平志，邓平，刘林.蜂窝网无线定位［M］.北京：电子工业出版社，2002.

［2］刘月华.时差定位无源雷达的系统设计［D］.南京：南京理工大学，2003.

［3］唐小明，何友.基于机会发射的无源雷达系统发展评述［J］.现代雷达，2002，24（2）：1-6.

［4］温中武，宋阔益.电子对抗中无源雷达的地位和发展前景［J］.国防科技，2007，1（9）：14-18.

［5］A.J.Weiss.Direct position determination of narrow band radio frequency transmitters［J］.IEEE Sig.Processing Lett，2004，（11）：672-681.

［6］J.J.Caffew.Wireless Location in CDMA Cellular Radio Systems［M］.Boston：Kluwer Academic Publisher，2000.

［7］C.Nerguizian，C.Despins and S.Affes.Geo-location in mines with an impulse response fingerprinting technique and neural networks［J］.IEEE Trans.Wireless Commun，2006（5）：603-611.

［8］L.Cong and W.Zhang.Hybrid TOA／AOA mobile user location for wideband CDMA cellular systems［J］.IEEE Trans.Wireless Commun，2002，（1）：439-447.

［9］R.I.Reza.Data fusion for improved TOA／TDOA position determination in wireless systems［D］.Ph.D.Dissertation，Virginia Tech，2000.

［10］H.V.Poor.An Introduction to signal detection and estimation［M］.New York：Springer-Verlag，1994.

［11］S.Al-Jazzar and J.J Caffery.ML and Bayesian TOA location estimators for NLOS environments［C］／／in Proc.IEEE Ini.Conf.Veh.Technol，Vancouver，BC，2002：1178-1181.

［12］Y.T Chan，Herman Yau Chin Hang，Pak-chung Ching.Exact and approximate maximum likelihood localization algorithms［J］.IEEE Trans on VTC，2006，55（1）：10-16.

［13］刘林，邓平，范平志.基于Chan氏算法和Taylor级数展开法的协同定位方法［J］.电子与信息学报，2004，26（1）：41-46.

［14］Oispuu M，Nickel U.Direct detection and position determination of multiple sources with intermittent emission［J］.Signal Processing，2010，90（12）：3056-3064.

［15］Weiss A J.Direct position determination of narrowband radio frequency transmitters［J］.IEEE Signal Processing Letters，2004，11（5）：513-516.

［16］A.Gernlani，C.Manes and P.Palunlbo.Polynomial extended Kalman filter［J］.IEEE Trans.AES，2005，（29）：1015-1022.

［17］K.Xiong，H.Y.Zhang and C.W.Chan.Performance evaluation of UKF-based nonlinear filtering［J］.Automatica，2006，（42）：261-270.

［18］C.Kwork，D.Fox and M.Meila.Real-time particle filters［J］.Proceedings of IEEE，2004，（92）：496-484.

［19］F.Gustafsson，F.Gunnarsson and N.bergman.Particle filters for positioning，navigation，and tracking［J］.IEEE Trans.SP，2002，（50）：425-426.

［20］Y.Bar-Shalom and W.D.Blair.Multitarget-multisensor tracking application and advances［M］.Boston：Artech House，2000.

［21］S.Deb.A generalized S-D assignment algorithm for multisensor-multitarget state estimation［J］.IEEE Trans.AES，1997，（33）：523-538.

［22］A.Poore and A.J.Robertson.A new class of lagrangian relaxation based algorithms for a class of multidimensional assignment problems［J］.Computational optimization and application，1997，（3）：544-563.

［23］K.R.Pattipati，S.Deb and Y.Bar-Shalom.A new relaxation algorithm and passive sensor data association［J］.IEEE Trans.Automatic Control，1992，（37）：198-212.

［24］T.K.Y.Bar-Shalom，X.Lin.Probabilistic data association techniques for target tracking with application to sonar，radar and EO sensors［J］.IEEE Journal of Oceanic Engineering，2005，（20）：37-55.

［25］尹成友.基于多传感器的近程目标高精度定位与跟踪的研究［D］.中国科学技术大学博士学位论文，2003.

［26］S.Theodoridis and K.Koutroumbas.模式识别［M］.北京：电子工业出版社，2006.

［27］戴邵武，马长里，代海霞.北斗双星／SINS组合导航中的捷联惯导算法研究［J］.计算机与数字工程，2010，38（2）.

［28］韩崇昭，朱洪艳，段战胜.多源信息融合［M］.北京：清华大学出版社，2006.