立式圆柱形储液罐的轴对称液固耦合模态分析
2013-11-20李金光
李金光
中国寰球工程公司 北京 100029
立式圆柱形钢制储液罐作为一种重要的储液容器,已广泛应用于石油化工行业的各个领域。国内工程界对储罐的设计、建造积累了丰富的工程经验,众多学者、工程师也对其特有的液固相互作用的动力特性展开了研究,取得了相应的研究成果:文献1建立了液固耦合的动力运动方程,采用Arnoldi方法分析储液容器的三维液固耦合动力特性问题;文献2采用强耦合法对储液容器流固耦合系统进行模态分析,并与附加质量法及文献计算结果进行了比较;文献3对立式圆柱形钢制储液罐的液固耦合问题,从理论分析出发,通过合理建模,利用ANSYS有限元软件对4种锚固式储油罐进行了模态分析;文献4讨论了储液罐的液固耦合有限元运动方程及其特性,介绍了利用ANSYS软件进行立式圆柱形储液罐的三维液固耦合模态分析的方法和注意事项,并以一个储液罐为例进行了计算。
纵观以上的研究成果,采用的技术手段都是建立三维有限元模型,进行液固耦合模态分析。三维有限元模型的液固耦合模态分析固然是最合理的且能反映储罐动力特性的分析方法,但由于三维模型的单元、节点较多,计算效率较为低下,所需的计算时间也较长;同时,随着储罐建设规模越来越大,三维有限元模型的规模也随之增大,再采用三维液固耦合的分析方法进行计算则会使计算效率更低。
ANSYS软件提供了轴对称模态分析的功能,可用来进行储液罐的液固耦合模态分析,用该方法不但可以达到与三维液固耦合模态分析相同的计算结果,还可以节省建模的计算时间,提高计算效率,下面就这一应用进行详细介绍。
1 液固耦合有限元运动方程
在进行液固耦合分析时,通常假定液体为无粘(忽略阻尼粘滞作用)、无旋、不可压缩和小幅度运动,固体为线弹性材料。液固耦合的模态分析特征值方程为[5]:
(1)
(2)

(3)

2 液固耦合模态分析在ANSYS中的实现
2.1 单元选择
利用ANSYS有限元软件进行轴对称液固耦合模态分析时,可用轴对称谐波封闭液体单元 FLUID81来模拟液体,该单元是对轴对称结构实体单元(PLANE25)做的修改(有4个节点,每个节点有X、Y和Z三个方向的平动自由度),可用于模拟装在容器内的无净流率的液体,可承受非轴对称荷载,特别适合于计算静水压力和液体与固体的相互作用,可计算加速度影响,如液体晃动问题,也能考虑温度的影响[6]。罐壁和底板可用轴对称谐波结构壳单元 Shell 61弹性壳单元模拟,该单元有4个节点,每个节点有4个自由度(X、Y和Z三个方向的平动自由度和绕Z轴的转动自由度),载荷可以是轴对称或非轴对称的。
2.2 求解方法
液固耦合的模态提取只能采用缩减法(Reduced/Householder)。缩减法通过采用主自由度和缩减矩阵来压缩问题的规模,利用HBI算法(Householder二分逆选代)计算特征值和特征向量。计算参数应设置频率提取数目和范围来分别提取液体晃动频率和液固耦合冲击频率,也可以不设置,这样就提取全部的频率。对缩减法而言,该方法求解的是主自由度的值,求解后应进行模态扩展将主自由度扩展到整个结构,且只有扩展的模态才能够进行图形显示[4]。
2.3 建模和前处理
在建立液固耦合有限元模型的过程中,下列六点应重点注意。
(1)储罐竖向坐标轴的设置:对于轴对称模型,储罐的竖向坐标轴应为Y轴方向,一般情况下液体的顶面应在Y=0处。
(2)KEYOPT(2)参数的设置: 当KEYOPT(2)=0时,表示在单元的每个面都放置重力弹簧;当KEYOPT(2)=1时,表示仅在Y=0处的单元面放置重力弹簧,这意味着液体的顶面应在Y=0处,不能出现Y向为正值的液体单元。
(3)加速度的设置:由于有自由面的存在,必须对所有单元设置垂直于自由面方向的加速度,可通过“acel”命令来施加。
(4)液固耦合交界面的处理:罐内液体与罐壁是两个相互独立的部分,应分别划分单元网格。在液固交界面上,液体单元节点坐标应与对应的罐壁单元节点的坐标重合。两个重合的节点仅在交界面处的法向方向进行位移耦合(强制法线方向的位移相同),而在切线方向不做约束。定义节点耦合用“CPINTF”命令来实现。
(5)主自由度的设置:由于模态提取采用缩减法(Reduced/Householder),所以必须定义主自由度。定义节点主自由度用“m”命令来实现。
(6)指定谐单元的非轴对称荷载项:由于模型采用的是谐波单元,其对应的外荷载是通过一系列的谐波函数来定义的,故应用“MODE”命令来指定荷载沿圆周向的谐波数及荷载的对称条件参数值ISYM(ISYM=1表示对称,ISYM=-1表示反对称)。
3 计算实例与结果分析
3.1 储液罐设计参数及有限元模型
储液罐容积为3000 m3,上部敞口(自由),下部固定在地面。直径D=20m,罐壁高H=12m,弹性模量Es=210GPa,泊松比v=0.26,密度ρs=7850kg/m3,壁厚t=8mm。
罐内液体液位高度h=10m,密度ρL=480kg/m3,体积模量EL=0.548GPa。
ANSYS中,储液罐的轴对称有限元计算模型见图1。

图1 罐体有限元模型
节点的液固耦合设置见图2,罐壁处的主自由度设置见图3。
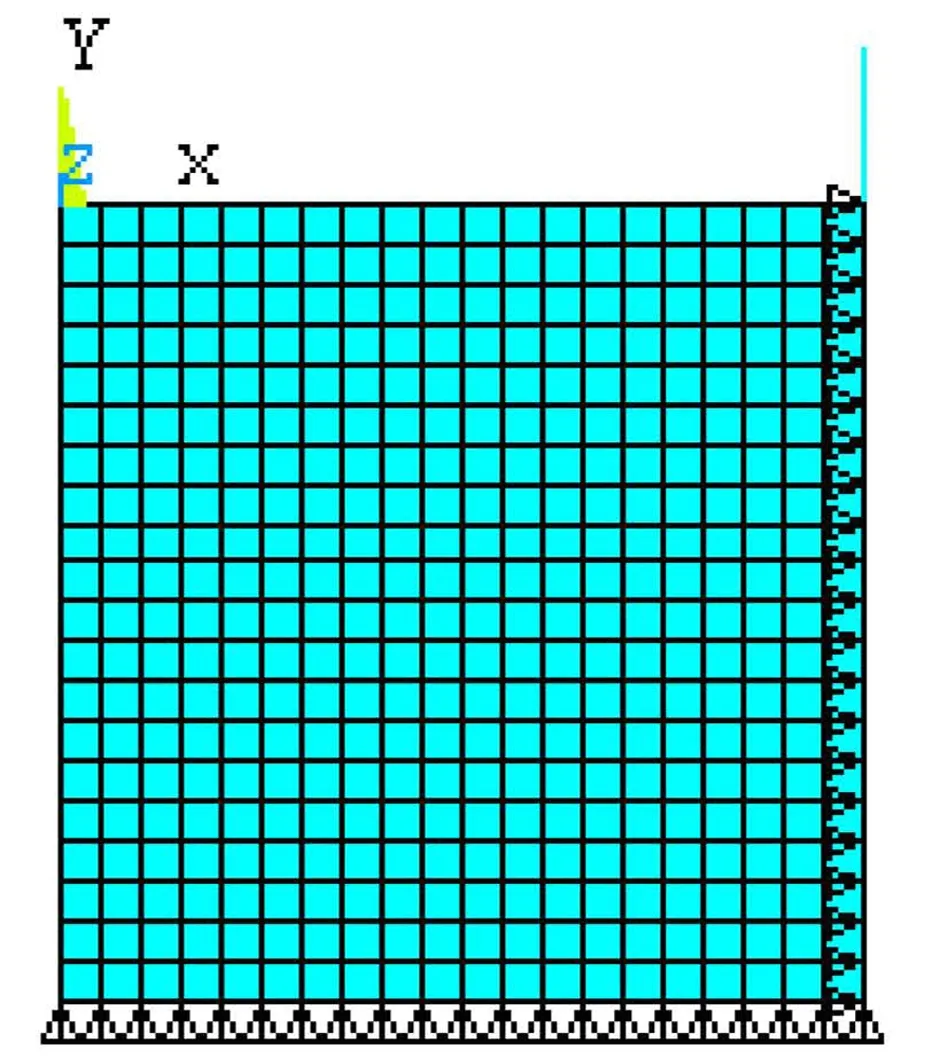
图2 液固耦合设置
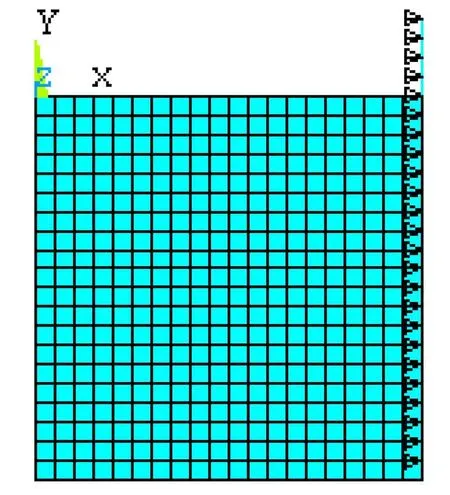
图3 罐壁处主自由度设置
3.2 计算结果与分析
虽然储罐晃动频率与液固耦合冲击频率相差比较大,但由于轴对称计算模型的节点数较少,故模态数不多,可直接设置一个较大的频率提取范围(涵盖晃动频率和液固耦合冲击频率),一次计算得到晃动模态和耦合振动模态。根据计算结果,其晃动模态和冲击模态见图4和图5。

图4 晃动模态视图

图5 冲击模态视图
表1给出了轴对称有限元分析得到的结果、文献4给出的三维有限元计算结果及依据文献7的公式得到的计算值。

表1 计算结果对比表
从表1可知,轴对称有限元液固耦合模态分析得到的计算结果与三维有限元液固耦合模态分析得到的计算结果比较一致,且与文献7的公式计算值也非常吻合。
4 结语
(1)利用ANSYS软件的轴对称谐波封闭流体单元 FLUID81进行立式圆柱形储液罐的轴对称液固耦合模态分析技术上是可行的。
(2)轴对称液固耦合模态分析与三维液固耦合模态分析的计算结果比较一致。
(3)轴对称液固耦合模态分析结果与文献7的公式计算值更为接近。
(4)轴对称液固耦合模态分析的计算效率要高于三维液固耦合模态分析。
参 考 文 献
1 徐 刚,任文敏,张 维等.储液容器的三维流固耦合动力特性分析 [J].力学学报,2004,36(3):328-335.
2 王 晖,陈 刚,张 伟等.储液容器三维流固耦合模态分析 [J].特种结构,2007,24(2):52-54.
3 潘 栋,邓民宪.基于ANSYS的储液罐固有振动特性分析 [J].西部探矿工程,2008,(5):52-54.
4 郑建华,李金光,唐辉永等.立式圆柱形储液罐的三维液固耦合模态分析[J].化工设计,2012,22(1):25-27.
5 朱伯芳.有限单元法原理与应用(第二版)[M].北京:中国水利水电出版社,1998.
6 ANSYS. Release 11.0 Documentation for ANSYS [CP]. ANSYS, Inc.
7 API 650-2009. Welded Steel Tanks for Oil Storage[S]. Washington:American Petroleum Institute,2009.
