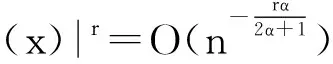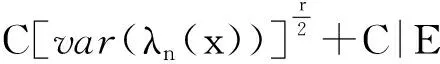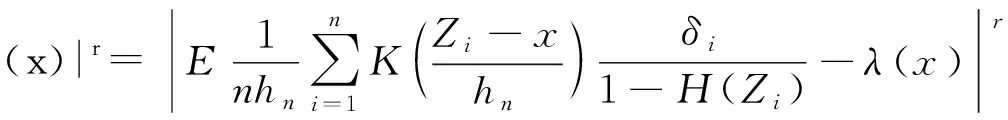强混合删失样本密度函数估计的r阶相合速度
2013-11-20曾翔
曾翔
(1.桂林理工大学广西矿治与环境科学实验中心,广西 桂林 541004;2.桂林理工大学理学院,广西 桂林 541004)
0 引言及定义
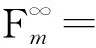
α(n),
若当n→∞时,α(n)→0,则称随机变量序列{Xn,n≥1}是α-混合或强混合,α(n)称为混合系数[1].
设生存时间{Xn;n≥1}是一列非负同分布的α-混合序列,分布函数为F(x),且F(0)=0,密度为f(x),删失时间{Yn;n≥1}是非负独立同分布的随机变量,其分布函数为G(y),且G(0)=0.假设随机变量Xi是独立于Yi的,我们不能完全观察到Xi,而只能观察到
Zi=min(Xi,Yi),δi=I(Xi≤Yi),
其中,I(·)表示事件的示性函数,称Zi是Xi被Yi随机删失的,Zi的分布函数为H=1-(1-F)(1-G).
在生存分析中,基于{(Zn,δn);n≥1}给出分布函数F(·)和G(·)的Kaplan-Meier估计[2]:
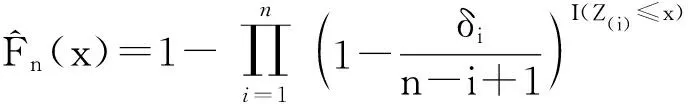
其中{Z(n);n≥1}是{Zn;n≥1}的次序统计量,δ(i)与Z(i)对应.
H的支撑为τH=inf{x:H(x)=1}≤∞,密度函数f(x)定义在(0,τH)上,其估计量fn(x)定义为:
(1)
对混合序列的研究已经有许多:文献[3]中给出了α-混合序列下的核密度估计量的强相合性与一致强相合性;Ye Daxiang等[4]讨论了α-混合随机变量几乎处处中心极限定理;刘君[5]研究了α-弱相依序列加权和的几乎处处中心极限定理;许冰[6]研究了α-混合序列的完全收敛性等.对删失数据的研究近些年也得到了广泛的关注,如徐芹[7]在{Xi}和{Yi}分别是独立随机变量时,研究了删失数据下线性回归模型的参数估计;薛留根[8]研究了删失数据下核密度估计的误差分布的强逼近等.但少见有文献对(1)式的相合性进行讨论,本文中研究了{Xi}为同分布α-混合序列,{Yi}为独立同分布序列时,fn(x)和λn(x)的r阶相合性,并给出r阶相合速度.
1 引理及定理
为了证明结论,假设以下基本条件成立:
(a)f(·)在[0,1]上满足α(α>0)阶Lipschitz条件;


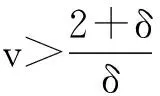
(e)对∀正整数j≥1,当随机变量X1取给定的值x1时,其条件概率密度记为fj(·|x1),对∀x∈R,x1x2∈U(x)(U(x)表示x的邻域),∃M0>0,fj(x2|x1)≤M0;
(f)设p=pn和q=qn是正整数,当n足够大时,有p+q≤n,qp-1≤c,phn→0.
本文中C是与n无关的正常数,即便在同一个式子中也可以表示不同的值.
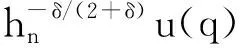
E|fn(x)-f(x)|r→0,n→∞.
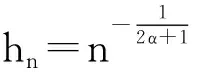
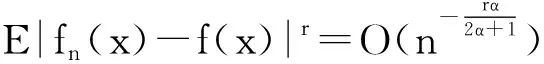
引理1[9]设{Xn,n≥1}是一列α-混合随机变量,混合系数是α(n),{Yn,n≥1}是一列独立同分布随机变量,{Xn,n≥1}与{Yn,n≥1}之间是独立的,则序列{(Xn,Yn),n≥1}是α-混合的,且混合系数是4α(n),特别地,Zn=min{Xn,Yn},n≥1也是α-混合的.
引理2[10]设随机变量X和Y满足E|X|p<∞,E|Y|q<∞,若p,q>1,p-1+q-1<1则有
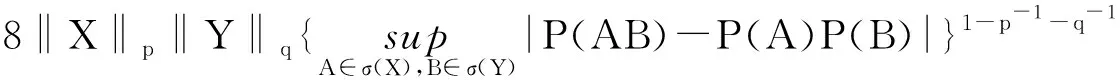
引理3满足条件(a)~(c),Z1,Z2,…,Zn…为同分布α-混合序列,G(x)在(0,τH)上连续,则
|Efn(x)-f(x)|r≤C|hn|αr.
引理3的证明由条件(a),∃M>0有
|f(x-hnu)-f(x)|≤M|hnu|α
(2)
由条件(b)~(c)和(2)式,可得

引理4假设条件(a)~(f)成立,Z1,Z2,…Zn…为同分布α-混合序列,则

引理4的证明注意到,



km=(m-1)(p+q),lm=(m-1)(p+q)+p+1,m=1,2,…,k.
则有
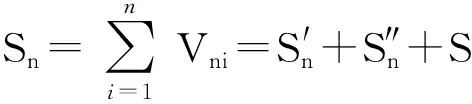
(3)

(4)
因为f与G在x的邻域是连续的,由条件(d)和引理2,有
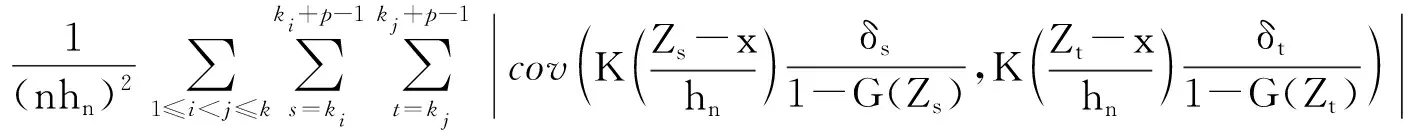
(5)
由条件(b),(e)~(f)以及f(·)在x的邻域是有界的,可得


(6)
注意到
(7)
由(7)式,我们可以得到
(8)
因此,由(4)~(6)式、(8)式,有
(9)
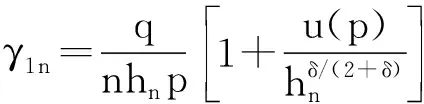
(10)
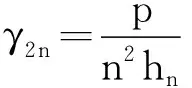

(11)
由(3)式、(9)~(11)式,得到
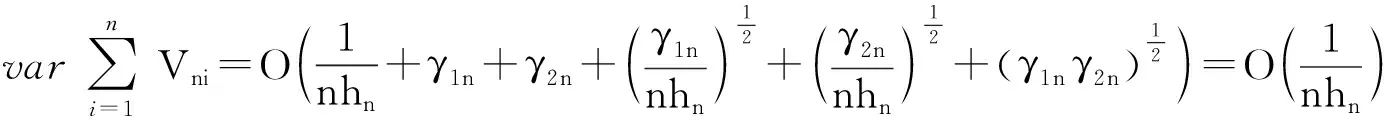
定理1的证明由于0 (12) 由引理3知 I2=C|Efn(x)-f(x)|r≤C(hn)αr→0,n→∞ (13) 由引理4知 (14) 综合(12)~(14)式即 E|fn(x)-f(x)|r→0,n→∞. 定理1证毕. (15) (16) 定理2在定理1条件下,设H(x)是定义在(0,τH)上的连续函数,则有 定理2的证明由(16)式,类似(12)式,有 (17) 由H(x)是定义在(0,τH)上的连续函数,类似(13)式证明过程,同理有: (18) 类比定理1中相应的证明,且由1-H(x)=(1-F(x))(1-G(x))可知: (19) 综合(17)~(19)式,类似(15)的证明过程,定理2得证. [1] Rosenblatt M. A central limit theorem and a strong mixing condition[J]. Proc Nat Acad Sc,1956,42:43-47. [2] Liang Hanying, Jacobo de Una-Alvarez. A Berry-Essen type bound in kernel density estimation for strong mixing censored samples[J]. Journal of Multivariate Analysis,2009,100:1219-1231. [3] George G Roussas. Asymptotic normality of the kernel estimate of a probability density function under association[J]. Statistics and Prob Lett,2000,50:1-12. [4] Ye Daxiang, Wu Qunying. Almost sure central limit theorem for product of partial sums of strongly mixing random variables[J]. Journal of Inequalities and Applications,2011,Article ID 576301,9 pages. [5] 刘君.弱相依序列加权和的几乎处处中心极限定理[J].吉林大学学报:理学版,2011,49(1):79-81. [6] 许冰.混合序列的完全收敛性[J].科学通报,1997,42(8):813-817. [7] 徐芹.删失数据下线性回归模型的参数估计[J].大学数学,2011,27(6):60-64. [8] 薛留根.删失数据下密度核估计的误差分布的强逼近[J].工程数学学报,2003,20(4):80-84. [9] Zongwu Cai. Asymptotic properties of Kaplan-Meier estimator for censored dependent data[J]. Statistics & Probability Letters,1998,37:381-389. [10] Hall P, Heyde C C. Martingale limit theory and its application[M]. New York: Academic Press,1980:278.

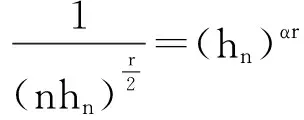
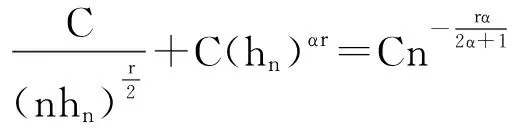
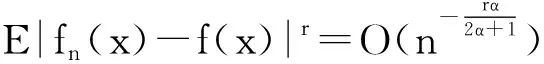
2 应用举例