基于遗传神经网络的钢管壁厚预测模型的研究

杨坤，李帅

(枣庄学院 机电工程学院，山东 枣庄 277160)

0 引言

钢管坯料经过穿孔后形成厚度不均的毛管.毛管轧制是热轧钢管生产的主要变形工序，其作用是使毛管壁厚接近或达到成品管壁厚和消除毛管在穿孔过程中产生的纵向壁厚不均.钢管的轧制过程对钢管壁厚的控制水平决定着钢管质量［1］. 钢管的轧制过程示意图如图1 所示:

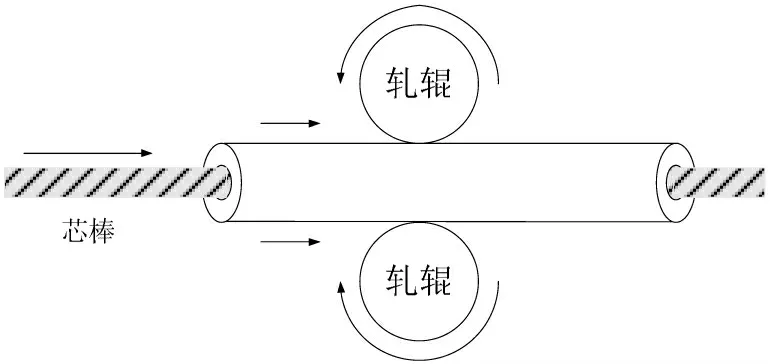
图1 钢管轧制过程示意图Fig 1 Schematic diagram of tube －rolling process

在不考虑温度影响、钢材塑性、机械间隙等因素影响的前提下，轧制后荒管壁厚的计算公式为:

其中，H为荒管壁厚，D为轧辊间距，d为芯棒直径.

钢管的轧制是一个非线性、快速、多变量耦合的复杂过程，实际数据表明通过这种常规线性计算公式得到的壁厚值与实际壁厚值之间存在较大的误差，难以满足实际的工艺要求.

近年来，基于BP 神经网络的预测模型在金属热加工业得到了广泛的应用［2－4］，BP 神经网络可从输入数据和输出数据之间所涉及的关系中进行“学习”，并通过观察重复发生的事件中获得经验，特别适合于同时考虑许多因素和条件、不精确和模糊的信息处理问题，具有非线性和自适应性等特点，利用BP 神经网络建立的模型具有较高的精度，但也存在着易陷入局部极小值等问题.本文采用遗传算法优化BP 神经网络的参数，解决基于BP 神经网络的模型在训练过程中存在的问题. 在实际样本数据的基础上利用这种遗传神经网络建立了钢管轧制前毛管五种工艺产生与轧制后荒管壁厚之间的数学模型，测试结果表明，这种模型对荒管壁厚的预测误差远小于常规荒管壁厚计算公式的计算误差，为钢管轧制工艺水平的提高提供了科学的依据.

1 基于BP 神经网络的钢管壁厚预测模型

BP 算法是一种误差反向传播式网络权值训练方法，也是一种比较成熟的神经网络计算算法，基于该算法的神经网络即为BP 神经网络［5］.BP 神经网络算法可以应用在钢管轧制这样多参数、非线性建模、难以建立起准确数学模型的复杂过程中，对钢管壁厚进行预测.

激活函数采用S(sigmoid)型函数:

假设钢管轧制过程中采集了P 组训练样本，以P 组训练样本输入的所有输出节点的误差平方和作为更新权值的指标，则有:

式中，m －输出层节点数;dj(k)－期望输出值;yj(k)－网络输出值.权值Wpq的调整采用梯度下降法，其调整量为:

通过计算可求得权值更新式:

式中，η－学习速率;δq(k)－误差项.为加快训练速度，在壁厚预测模型神经网络权值更新式加入动量项，更新式变为:

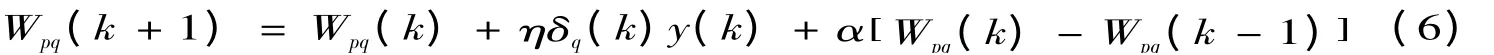
图2 BP 神经网络的结构Fig.2 Structure of BP neural network

在钢管壁厚预测中设计一个三层的神经网络，选择在钢管轧制前荒管的毛管温度、长度、外径、轧辊转速、芯棒直径五项工艺参数作为模型的输入，钢管轧制后毛管的壁厚作为模型的输出.模型结构如图2 所示.已经证明［6］对于在任何闭区间内的一个连续函数都可以用一个隐层的BP 神经网络来逼近，因而一个三层的BP 神经网络可以完成任意的n 维到m 维的映射，基于BP 神经网络的钢管壁厚模型是可行的.虽然BP 算法经过了不断的改进，但在这种算法过程中中仍存在一些缺点，如:需要较长的训练时间、不能完全训练和易陷入局部极小值等，这些缺点对基于BP 神经网络算法的钢管壁厚预测模型造成了很多不利的影响.

2 遗传算法优化神经网络模型

2.1 采用遗传优化神经网络模型参数

根据钢管壁厚预测问题的需要，选用多输入单输出的BP 神经网络.鉴于遗传算法具有全局寻优能力，可防止陷入局部极小点，以及BP 算法依梯度下降搜索法保证在有限次搜索后快速找到全局最优的特点，

本文将二者结合起来，GA 的适应度评价函数是:

BP 神经网络的网络结构参数主要有隐含层数、隐含层节点数、学习率和动量因子.其中隐含层及其节点数表征了网络学习输入信息的充分程度，可以根据经验公式来确定.学习率是网络学习速度的量度，动量因子可以抑制振荡的发生.

2.2 参数设定

根据经验公式m = fix［log2n］+1 来确定神经网络隐含层神经元个数，这里，m表示隐含层神经元个数;n表示学习样本数目;fix()表示取整操作.在钢管壁厚预测模型训练中采集了50 组数据，将其中的40 组作为学习样本，根据公式选择的隐含层神经元个数m=6.在训练前根据样本数据产生不同实数区间内取值的神经网络初始权值.

3 模型的训练与仿真

根据上文所述，在MATLAB7.0 上编写基于遗传神经网络的钢管壁厚预测模型的源程序.对不同批次的钢管轧制前毛管的温度、长度、外径、轧辊转速、芯棒直径和轧制后荒管壁厚等工艺参数进行采集，共得到50 组原始数据.编号为1—50，将其中的1 －40 号数据作为训练样本，41 －50 号数据作为测试样本. 将1 －40 号训练样本输入模型中进行训练，确定模型的各个参数.为验证模型的有效性，将41 －50 号样本输入建立的模型中进行检验，与实际数据和经验公式计算结果相比较，具体结果如表1 所示.

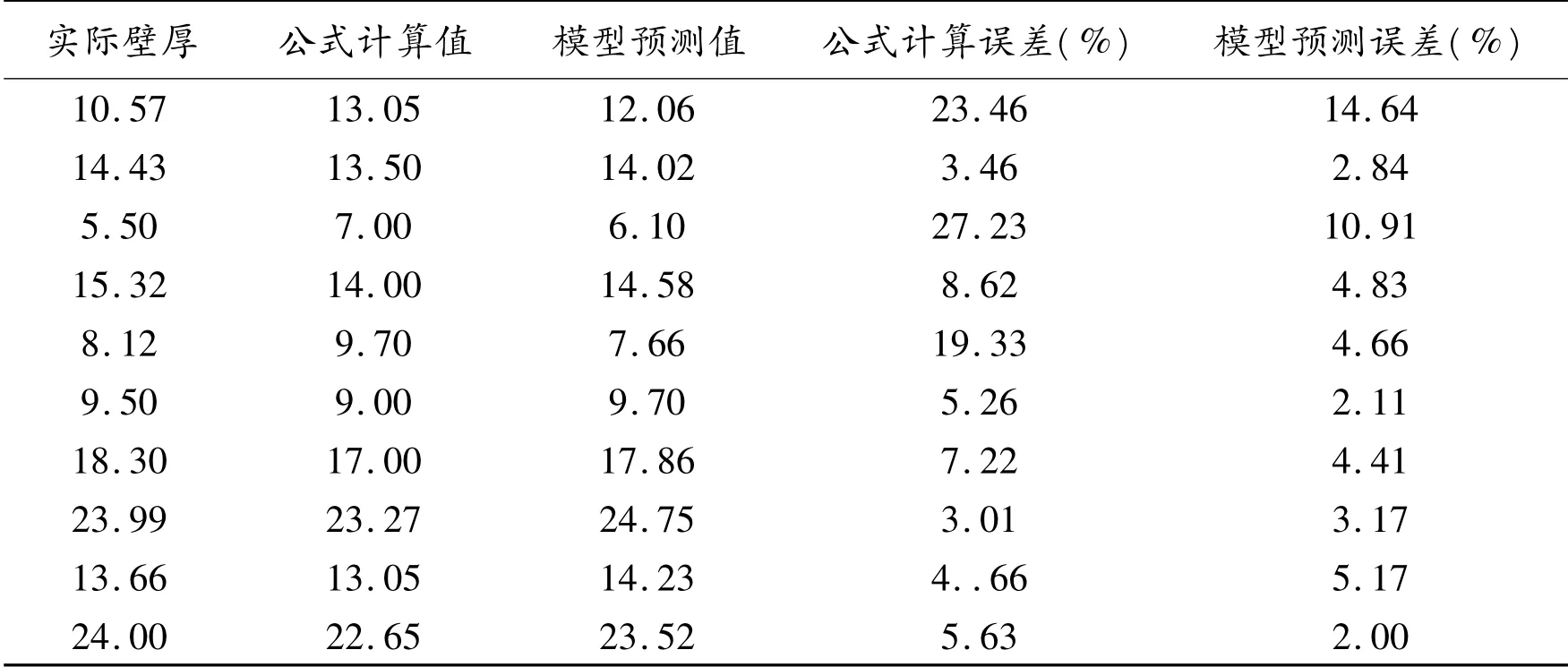
表1 模型预测值与公式计算值比较Table 1 Compared between model predictive values and the calculated values

如上表所示，利用基于遗传神经网络的壁厚预测模型预测的误差与实际壁厚之间的最小误差2.00%，最大误差14.64%;利用常规壁厚计算公式计算的钢管轧制后荒管的壁厚与实际壁厚之间的最小误差3.46%，最大误差27.23%.对同一钢管壁厚的预测误差均小于常规公式的预测误差.

［1］刘涛，刘晓敏，赵海娇，等.最新无缝钢管生产新工艺新技术与质量控制检验实用手册［M］.北京:北方工业出版社2006.

［2］罗小波，赵文雅，饶建华.基于BP 神经网络的CCT 曲线预测研究［J］.热加工工艺，2008，37(22):85 －87.

［3］李春天，罗怡.非等厚异种钢电阻点焊焊点成形及神经网络预测［J］.热加工工艺，2009，38(1):121 －123.

［4］刘晓燕，赵西成，姚筱春.人工神经网络在硼钢淬透性预测中的应用［J］.热加工工艺，2004，33(10):20 －21.

［5］郭俊卿，陈拂晓，李合军，等，铅黄铜超塑性能的人工神经网络预测［J］.热加工工艺，2008，37(14):92 －95.

［6］Hayakawa T，Haddad W M，Hovakimyan N. Neural network adaptive control for a class of nonlinear uncertain dynamical systems with asymptotic stability guarantees［J］. IEEE Trans－actions on Neural Networks，2008，19(1):80 －89.

［7］Fabri S，Kadirkamanathan V. Dynamic structure neural networks for stable adaptive control of nonlinear systems［J］.IEEE Transactions on Neural Networks，1996，7(5):1151 －1167.

［8］刘威，李小平，毛慧欧，等.基于实数编码遗传算法的神经网络成本预测模型及其应用［J］.控制理论与应用，2004，21(3):423 －426.