幂级数在条件数列中的应用

陈引兰，余立婷

(湖北师范学院 数学与统计学院，湖北 黄石 435002)

文[1]中介绍了幂级数的相关知识，幂级数是一类简单而有用的函数项级数。在文[2]中，美国数论专家Smrandache F提出了初等数论及集合论中105个未解决的问题让大家研究，其中有5个问题是关于数列的性质问题，可见对数列的研究非常重要。

本文先定义了条件数列，利用若干基本初等函数的幂级数展开式的变形，发现了条件数列求和规律，给出了通过其他方法较难证明的条件数列和的代数恒等式，结果以定理1-6给出。定理7是文[3]中的定理3和定理4的一个推广，即文[3]中的定理3和定理4是本文定理7的推论，并给出了证明，这一部分的推广还给出了求其他条件数列和的方法。接着利用这些恒等式，讨论了通项是条件数列求和的正项级数的敛散性，而这些级数的敛散性用其他方法也不易判断。

为了下面叙述的方便，先给出条件数列的定义。

定义1 当一个数列的通项的序满足一个特定的不定方程式时，把它叫做条件数列。称条件数列的通项的序满足的不定方程中的未知数个数为条件数列的项，称条件数列的通项中各未知数的最高次数为条件数列的次数。

1 若干条件数列求和的恒等式

1.1 一次二项、一次三项、一次四项条件数列求和

下面的定理1和定理2是一次二项条件数列求和.

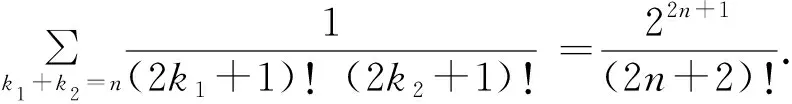
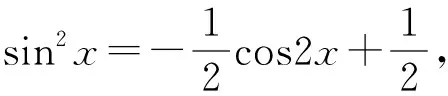
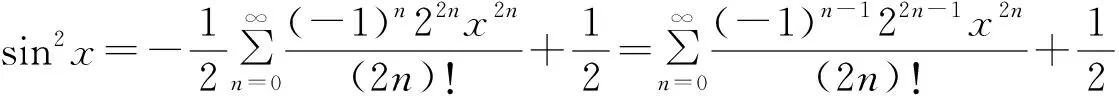
(1)

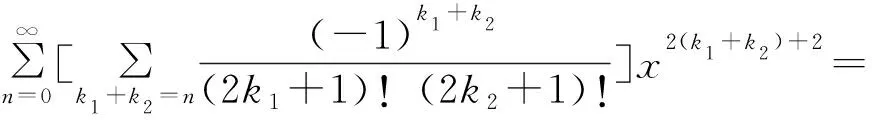
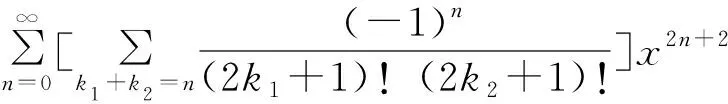
(2)

比较(1),(2) 式中x2n+2的系数可得

所以

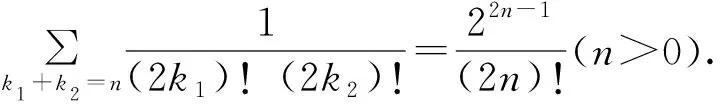
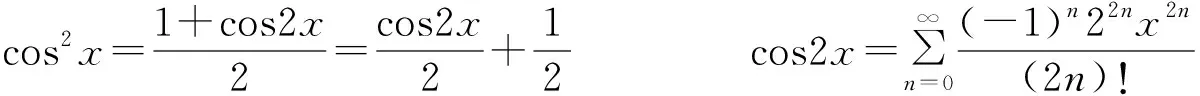
所以

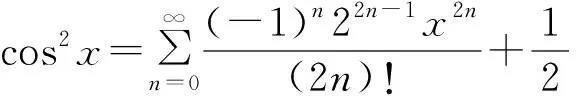
(3)

又由幂级数乘法知

(4)

比较(3)(4) 式中的x2n的系数知

所以

下面的定理3和定理4是一次三项条件数列求和。

定理3 设k1,k2,k3,n为自然数，则有

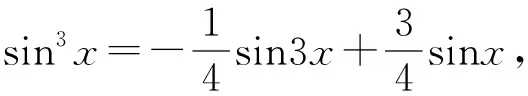
可得

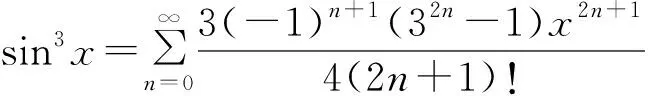
(5)

又由幂级数的乘法知，

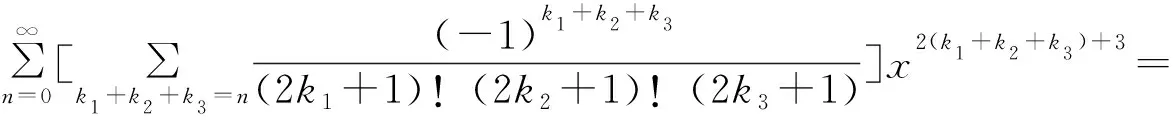
(6)

比较 (5)(6)式中x2n+3的系数可得

所以

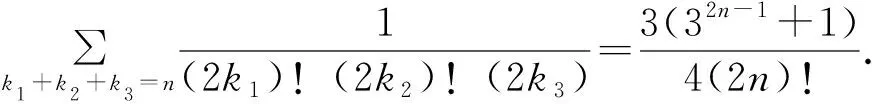
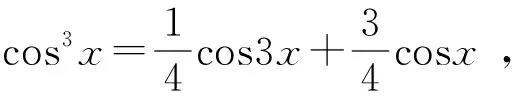
(7)

再由幂级数的乘法得

(8)

比较(7)(8) 式中x2n的系数可得

下面的定理5和定理6是一次四项条件数列求和。

定理5 设k1,k2,k3,k4,n为自然数，则有

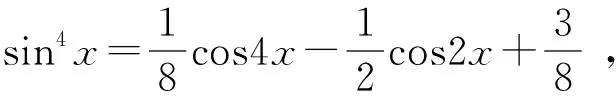
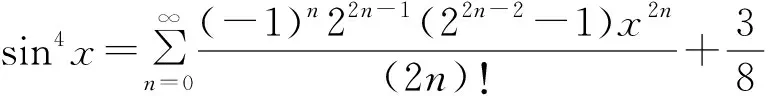
(9)

由幂级数乘法知：

(10)

比较(9),(10) 式中x2n+4的系数知

定理6 设k1,k2,k3,k4,n为自然数，则有

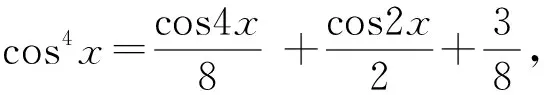
(11)

又由幂级数的乘法

(12)

比较(11),(12) 式中x2n的系数可得

注 定理1～6的推广：定理1～6只是给出了通项中分母同时是奇数的阶乘或者同时是偶数阶乘的条件数列求和恒等式，如果需要分母中是若干个奇数的阶乘和偶数的阶乘求和的对应项恒等式，则可以利用相应的三角函数的恒等变形和它们的幂级数展开式，比较左右两边幂级数展开式的系数，求出条件数列求和的恒等式。

1.2 二次s项条件数列乘积和的恒等式

定理7 设k1,k2,k3,…ks,n,j为自然数，s为大于 1的自然数，则有

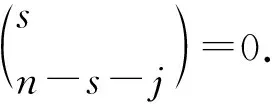
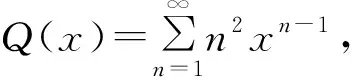
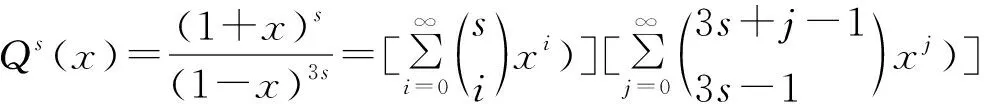
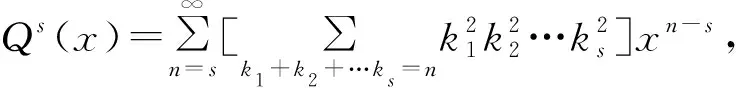
令s=2,3，分别得到下面的推论1,2.

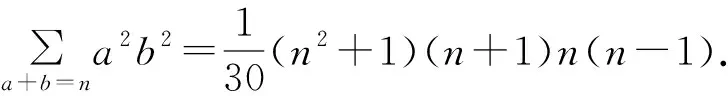
推论2[3]设a,b,c,n为自然数，则有

2 若干通项是条件数列的正项级数的收敛性

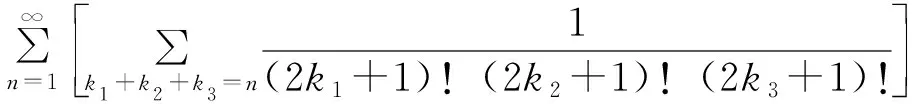
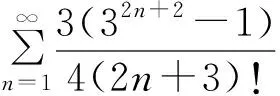
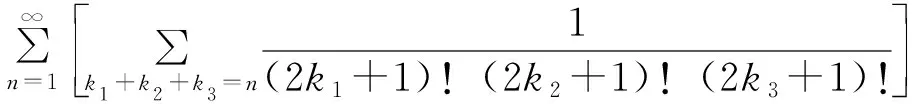
是收敛的。

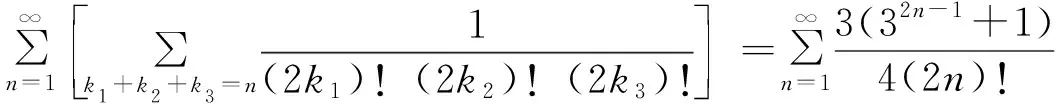
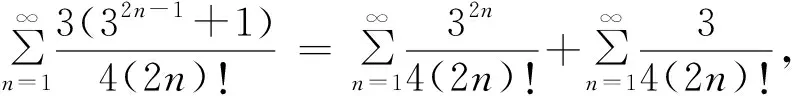
证明 由定理5知

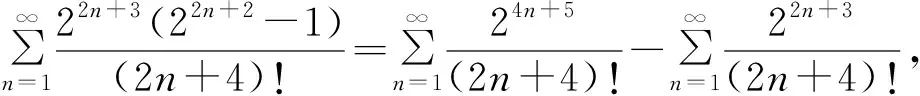
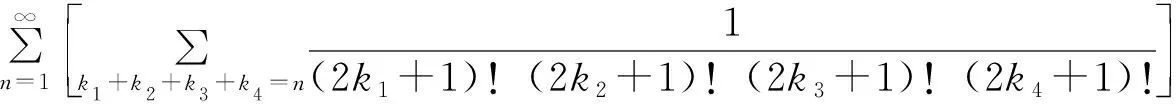
是收敛的。

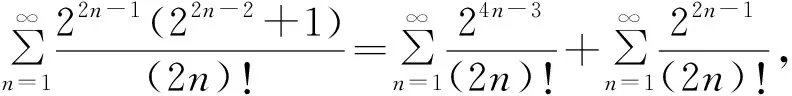
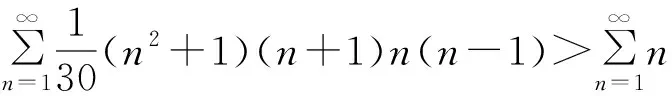
证明 由定理7的推论2知

所以

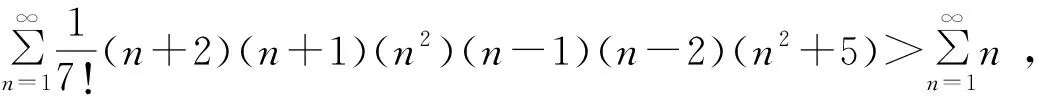
参考文献：

[1]华东师范大学数学系.数学分析(第四版)[M].北京:高等教育出版社.2010.

[2]Florentin Smarandche Only problems Not solutioned [M].大连：Xiquan Publishing House,1993.

[3]王永兴，杨倩丽.关于幂级数在自然数列中的应用[J].渭南师范大学学报，2005,20(5):19～21.

[4]徐利治.数学分析的方法及例题选讲——分析学的思想、方法与技巧[M].大连:大连理工大学出版社，2008.